控制系统微分方程是在时间域描述系统动态性能的数学模型,在给定外作用及初始条件下,求解微分方程可以得到系统的输出响应。
应用微分方程列写控制系统数学模型的方法比较直观,对于复杂的高阶微分方程,特别适合于计算机编程求解,采用迭代的方法循环计算一定时间后获得输出量波形曲线。缺点是系统结构改变或某个参数改变时,需要重新列写并求解微分方程,才能获得系统的性能指标数据,不方便系统的分析和设计。
用拉氏变换法求解线性系统微分方程时,可以获得控制系统在复数域的数学模型,即传递函数,传递函数可以表征系统的动态性能,并且可以在不求系统输出解的情况下,研究系统的结构或参数变化时系统性能指标,特别适合于不借助于计算机情况下分析和设计控制系统的性能,当然,也可以利用MATLAB进行系统性能分析,由此可见,传递函数是经典控制理论中最基本和最重要的概念。
1.传递函数概念
定义:线性定常系统的传递函数,定义为零初始条件下,系统输出量的拉氏变换与输入量的拉氏变换之比;
设线性定常系统的n阶微分方程为:
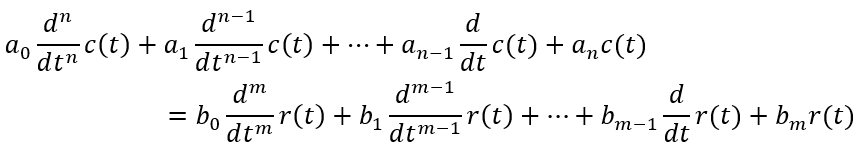
这里,c(t)是系统输出量,r(t)是系统输入量,ai,bj是与系统结构和参数有关常系数;
在零初始条件下,即输入量和输出量及其各阶导数在t=0时的值均为0;对上式两侧分别求取拉氏变换,可获得s的代数方程为:
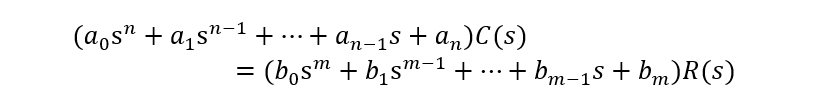
于是,可求出系统传递函数为:
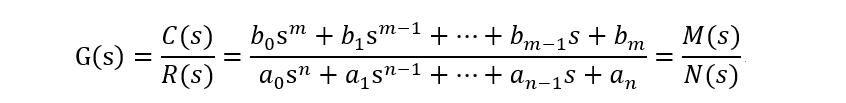
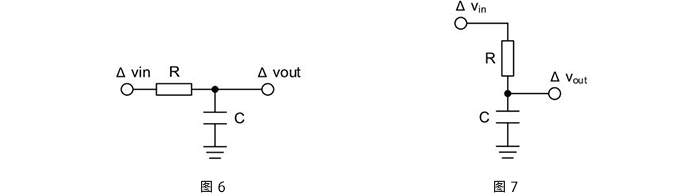
已知RLC串联无源网络,求电容电压Uo(s)与输入电压Ui(s)之间的传递函数
RLC网络电容电压微分方程为:
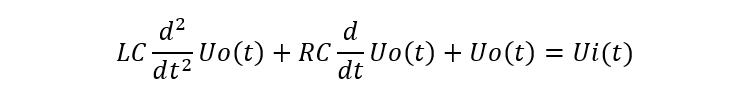
在零初始条件下,对上式中各项求拉氏变换,可得到关于s的代数方程,
令Uo(s)=L[Uo(t)],Ui(s)=L[Ui(t)],则关于s的代数方程为:
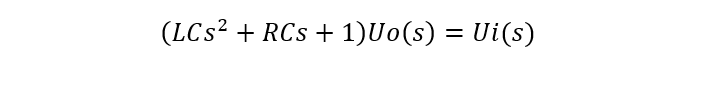
根据传递函数的定义,系统输出量的拉氏变换与输入量的拉氏变换比值为:
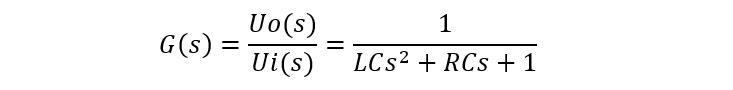
传递函数示意图如下:

-
控制系统
+关注
关注
41文章
6666浏览量
110945 -
计算机
+关注
关注
19文章
7550浏览量
88753 -
编程
+关注
关注
88文章
3642浏览量
94046 -
传递函数
+关注
关注
0文章
102浏览量
14010 -
数学模型
+关注
关注
0文章
83浏览量
11994
发布评论请先 登录
相关推荐
放大器的传递函数-误差放大器、电压放大器、电流放大器的传递函数导出
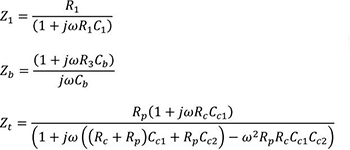


误差放大器、电压放大器、电流放大器的传递函数导出
传递函数前言
传递函数和导出的基本概念
DC/DC转换器的电源传递函数详细介绍
传递函数极点和零点的影响是什么
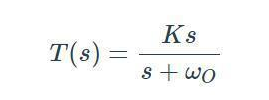
传递函数的频率特性
传递函数的定义是什么 传递函数的拉氏反变换是什么响应
调制传递函数的基本原理简析




 传递函数的概念
传递函数的概念
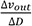










评论