汇总几个在算法题以及工程开发中常用的位运算技巧

位操作（Bit Manipulation）可以有很多技巧，有一个叫做 Bit Twiddling Hacks 的网站收集了几乎所有位操作的黑科技玩法

但是这些技巧大部分都过于晦涩，我觉得可以作为字典查阅，没必要逐条深究。但我认为那些有趣的、有用的位运算技巧，是我们每个人需要掌握的。

所以本文由浅入深，先展示几个有趣（但没卵用）的位运算技巧，然后再汇总几个在算法题以及工程开发中常用的位运算技巧。

几个有趣的位操作

利用或操作`|`和空格将英文字符转换为小写

('a'|'')='a'
('A'|'')='a'

利用与操作`&`和下划线将英文字符转换为大写

('b'&'_')='B'
('B'&'_')='B'

利用异或操作`^`和空格进行英文字符大小写互换

('d'^'')='D'
('D'^'')='d'

以上操作能够产生奇特效果的原因在于 ASCII 编码。ASCII 字符其实就是数字，恰巧空格和下划线对应的数字通过位运算就能改变大小写。有兴趣的读者可以查 ASCII 码表自己算算，本文就不展开讲了。

不用临时变量交换两个数

inta=1,b=2;
a^=b;
b^=a;
a^=b;
//现在a=2,b=1

加一

intn=1;
n=-~n;
//现在n=2

减一

intn=2;
n=~-n;
//现在n=1

判断两个数是否异号

intx=-1,y=2;
booleanf=((x^y)< 0); // true

int x = 3, y = 2;
boolean f = ((x ^ y) < 0); // false

如果说前 6 个技巧的用处不大，这第 7 个技巧还是比较实用的，利用的是补码编码的符号位。整数编码最高位是符号位，负数的符号位是 1，非负数的符号位是 0，再借助异或的特性，可以判断出两个数字是否异号。

当然，如果不用位运算来判断是否异号，需要使用 if else 分支，还挺麻烦的。你可能想利用乘积来判断两个数是否异号，但是这种处理方式容易造成整型溢出，从而出现错误。

index & (arr.length - 1) 的运用

我在单调栈解题套路中介绍过环形数组，其实就是利用求模（余数）的方式让数组看起来头尾相接形成一个环形，永远都走不完：

int[]arr={1,2,3,4};
intindex=0;
while(true){
//在环形数组中转圈
print(arr[index%arr.length]);
index++;
}
//输出：1,2,3,4,1,2,3,4,1,2,3,4...

但模运算%对计算机来说其实是一个比较昂贵的操作，所以我们可以用&运算来求余数：

int[]arr={1,2,3,4};
intindex=0;
while(true){
//在环形数组中转圈
print(arr[index&(arr.length-1)]);
index++;
}
//输出：1,2,3,4,1,2,3,4,1,2,3,4...

简单说，& (arr.length - 1)这个位运算能够替代% arr.length的模运算，性能会更好一些。

那问题来了，现在是不断地index++，你做到了循环遍历。但如果不断地index--，还能做到环形数组的效果吗？

答案是，如果你使用%求模的方式，那么当index小于 0 之后求模的结果也会出现负数，你需要特殊处理。但通过&与运算的方式，index不会出现负数，依然可以正常工作：

int[]arr={1,2,3,4};
intindex=0;
while(true){
//在环形数组中转圈
print(arr[index&(arr.length-1)]);
index--;
}
//输出：1,4,3,2,1,4,3,2,1,4,3,2,1...

我们自己写代码一般用不到这个技巧，但在学习一些其他代码库时可能会经常看到，这里留个印象，到时候就不会懵逼了。

n & (n-1) 的运用

n & (n-1)这个操作在算法中比较常见，作用是消除数字n的二进制表示中的最后一个 1。

看个图就很容易理解了：

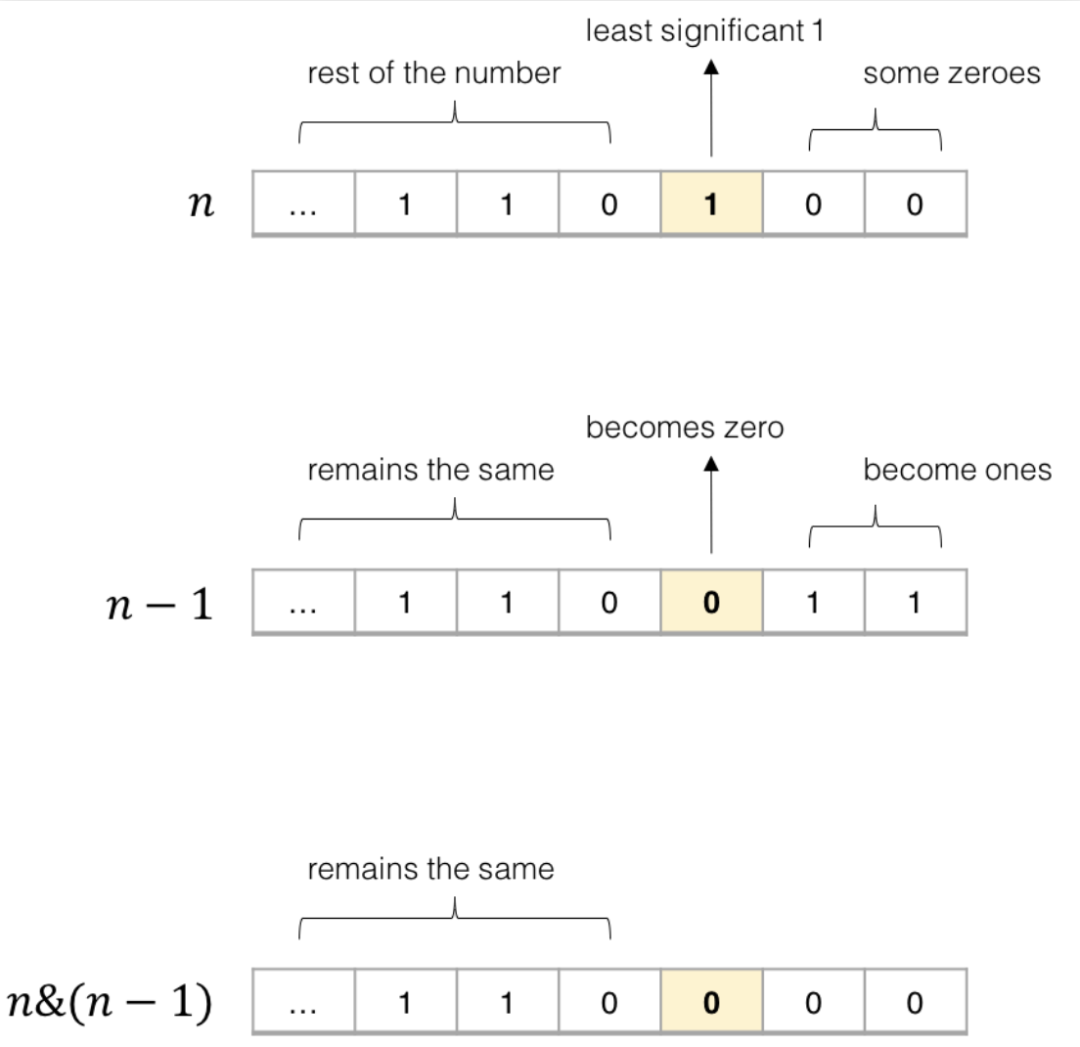
其核心逻辑就是，n - 1一定可以消除最后一个 1，同时把其后的 0 都变成 1，这样再和n做一次&运算，就可以仅仅把最后一个 1 变成 0 了。

1、计算汉明权重（Hamming Weight）

这是力扣第 191 题「位 1 的个数」：

就是让你返回n的二进制表示中有几个 1。因为n & (n - 1)可以消除最后一个 1，所以可以用一个循环不停地消除 1 同时计数，直到n变成 0 为止。

inthammingWeight(intn){
intres=0;
while(n!=0){
n=n&(n-1);
res++;
}
returnres;
}

2、判断一个数是不是 2 的指数

力扣第 231 题「2 的幂」就是这个问题。

一个数如果是 2 的指数，那么它的二进制表示一定只含有一个 1：

2^0=1=0b0001
2^1=2=0b0010
2^2=4=0b0100

如果使用n & (n-1)的技巧就很简单了（注意运算符优先级，括号不可以省略）：

booleanisPowerOfTwo(intn){
if(n<= 0) return false;
    return (n & (n - 1)) == 0;
}

a ^ a = 0 的运用

异或运算的性质是需要我们牢记的：

一个数和它本身做异或运算结果为 0，即a ^ a = 0；一个数和 0 做异或运算的结果为它本身，即a ^ 0 = a。

1、查找只出现一次的元素

这是力扣第 136 题「只出现一次的数字」：

对于这道题目，我们只要把所有数字进行异或，成对儿的数字就会变成 0，落单的数字和 0 做异或还是它本身，所以最后异或的结果就是只出现一次的元素：

intsingleNumber(int[]nums){
intres=0;
for(intn:nums){
res^=n;
}
returnres;
}

2、寻找缺失的元素

这是力扣第 268 题「丢失的数字」：

给一个长度为n的数组，其索引应该在[0,n)，但是现在你要装进去n + 1个元素[0,n]，那么肯定有一个元素装不下嘛，请你找出这个缺失的元素。

这道题不难的，我们应该很容易想到，把这个数组排个序，然后遍历一遍，不就很容易找到缺失的那个元素了吗？

或者说，借助数据结构的特性，用一个 HashSet 把数组里出现的数字都储存下来，再遍历[0,n]之间的数字，去 HashSet 中查询，也可以很容易查出那个缺失的元素。

排序解法的时间复杂度是 O(NlogN)，HashSet 的解法时间复杂度是 O(N)，但是还需要 O(N) 的空间复杂度存储 HashSet。

这个问题其实还有一个特别简单的解法：等差数列求和公式。

题目的意思可以这样理解：现在有个等差数列0, 1, 2,..., n，其中少了某一个数字，请你把它找出来。那这个数字不就是sum(0,1,..n) - sum(nums)嘛？

intmissingNumber(int[]nums){
intn=nums.length;
//虽然题目给的数据范围不大，但严谨起见，用long类型防止整型溢出
//求和公式：(首项+末项)*项数/ 2
longexpect=(0+n)*(n+1)/2;
longsum=0;
for(intx:nums){
sum+=x;
}
return(int)(expect-sum);
}

不过，本文的主题是位运算，我们来讲讲如何利用位运算技巧来解决这道题。

再回顾一下异或运算的性质：一个数和它本身做异或运算结果为 0，一个数和 0 做异或运算还是它本身。

而且异或运算满足交换律和结合律，也就是说：

2^3^2=3^(2^2)=3^0=3

而这道题索就可以通过这些性质巧妙算出缺失的那个元素，比如说nums = [0,3,1,4]：

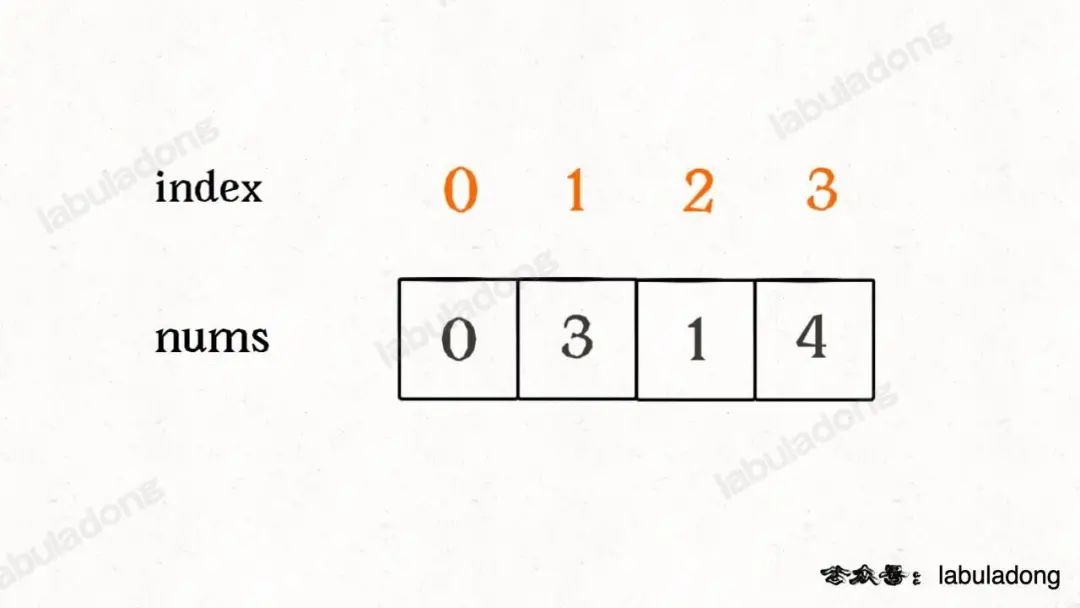
为了容易理解，我们假设先把索引补一位，然后让每个元素和自己相等的索引相对应：

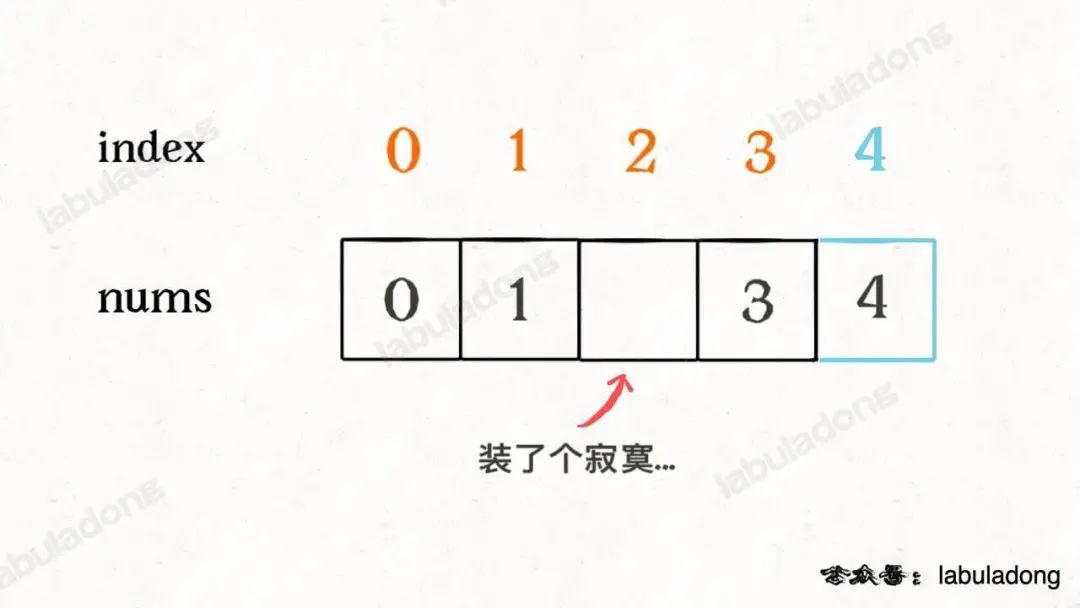
这样做了之后，就可以发现除了缺失元素之外，所有的索引和元素都组成一对儿了，现在如果把这个落单的索引 2 找出来，也就找到了缺失的那个元素。

如何找这个落单的数字呢，只要把所有的元素和索引做异或运算，成对儿的数字都会消为 0，只有这个落单的元素会剩下，也就达到了我们的目的：

intmissingNumber(int[]nums){
intn=nums.length;
intres=0;
//先和新补的索引异或一下
res^=n;
//和其他的元素、索引做异或
for(inti=0;i< n; i++)
        res ^= i ^ nums[i];
    return res;
}

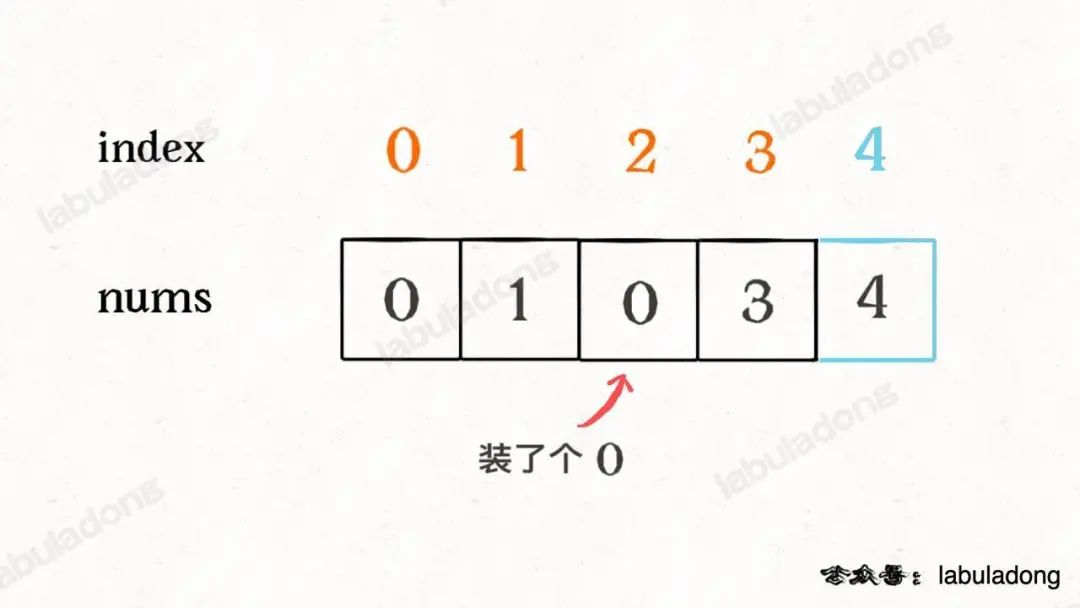
由于异或运算满足交换律和结合律，所以总是能把成对儿的数字消去，留下缺失的那个元素。

到这里，常见的位运算差不多都讲完了。这些技巧就是会者不难难者不会，也不需要死记硬背，只要有个印象就完全够用了。

审核编辑：刘清