点击蓝字关注我们
在使用数据表中的热特性参数时,如何做出设计决策经常存在一定的误区。本文将帮助您了解如何解读数据表中的热参数:包括如何选择 θ 与 ψ 及其计算,以及如何以实用的方式将其应用于设计,这里我们将重点讨论在稳态工作条件下的情况。
定义环境温度TA
所有热量最终到达的环境的温度,环境在热意义上“远离”器件。
外壳温度TC
器件外部“壳体”上代表点的温度;使用任何基于此值的参数时,代表点的位置必须明确定义。
结温TJ
半导体器件内部最热点的温度。
ψ-JT
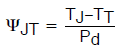
热特性参数,在结至外壳顶部(TT)之间测量
ψ-Jx
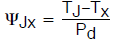
热特性参数,在结至指定位置(Tx)之间测量
ψ-xA
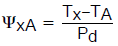
热特性参数,在指定位置(Tx)至环境之间测量
θ-JA
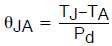
器件加外部系统的总热阻
θ-Jc
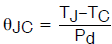
理想情况下,仅器件的热阻(测量到外壳)
Pd
器件总功耗
最小焊盘
参考热测试板,电路板仅有为了安装器件并向/从器件传输电源和信号所需的最少量金属焊盘和走线;走线实际上可能有比安装焊盘本身大得多的面积,而且电路板的总尺寸及其厚度可能与实际应用中使用的明显不同。这些变量只是使数据表中的最小焊盘值在实际应用环境中用于有限用途的部分变量。
1英寸焊盘
参考热测试板,电路板具有标称 1 平方英寸的镀铜面积,在其中心安装有封装;通常,向/从器件传输电源和信号所需的额外走线面积只是焊盘的一小部分(<10%);但对于较大的器件,如 D2pak,实际散热器本身可能占到 1 平方英寸的很大一部分,因此对于较大器件而言,最小焊盘与 1 英寸焊盘值之间的差异不像小型器件那么大。铜基板厚度、电路板总尺寸和厚度,可能会使该值与实际应用中的值显著不同。这些变量只是使数据表中的 1 英寸焊盘值在实际应用环境中用于有限用途的部分变量。
稳态数据
所谓“稳态”,指的是这样的工作条件:每个相关器件的功耗已保持足够长时间的稳定,使得温度变化不再发生。从零功率开始,所有温度最初都处于环境温度,突然施加恒定的非零功率将导致温度单调升高。因此,最终会在稳态下达到最高温度。稳态热特性数据通常以热阻或阻抗的具体值的形式提供。此外,也可以提供其他图表,显示稳态热特性通常如何依赖于某些外部条件,例如特定器件的应用板上提供了多少散热金属。对于多结器件,也可能存在稳态热特性的矩阵形式。
θ和ψ数据
θ,有时表示为Rθ,其值是真正的“热阻”。也就是说,如果知道两点的温度,那么从一点流向另一点的热量完全由该热阻决定。反之,如果知道沿该路径的热流量,并且知道其热阻,那么就能预测此热流将会导致的温差。如果系统中有其他热路径,这些热路径有自己的特性,它们与我们关注的特定路径上发生的事情无关。单位通常是°C/W。
在半导体封装和器件领域,通常最多有两个“真正”的热阻,即θ-JA 和θ-JC,必须仔细定义这些热阻。但是,关于这些值的最重要的一个事实是,器件消耗的总功率在所述的两个“点”之间流动(结是一个“点”,环境温度或外壳温度是另一个“点”)。也就是说,系统中没有无关的平行热路径让一些热量“泄漏”出去。所有离开结的热量,最终都到达或经过另一个点——环境或外壳。
数学上将这两个量定义如下:
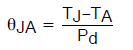
 (公式1)
(公式1)

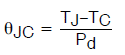 (公式2)
(公式2)
因此,知道相应的值后,实际工作结温可根据下式进行预测:

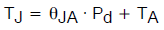 (公式3)
(公式3)
或

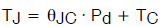 (公式4)
(公式4)
对于θ-JA,显然,根据定义,所有离开结的功率最终都会到达环境,因此该温差与封装总功率之比是一个真正的系统热阻。数据表可能为不同的代表性安装情况提供一个或多个θ-JA 值。例如,最小焊盘板值和 1 英寸焊盘板值,或者可能是θ-JA 与铜基板面积的关系图。但即使铜面积是“正确的”,这些值也可能不适用于实际应用。其他变量,如其他功耗器件的存在、气流条件的性质、铜基板本身的厚度和详细布局,都会影响该值。
对于θ-JC,两个点是结(J)和“外壳”(C)——这里的挑战在于“外壳”温度的定义或选择。如果我们有理由假设 100%的功耗实际上都流过我们定义的“C”点,那么此温差与封装总功率之比就是一个真正的热阻。
通常,唯一能够合理接近该 100%热条件的测试情况是冷板测试,并且功率封装要直接夹到冷板上,还必须仔细指定“外壳”测量的位置。
为了获得良好的θ-JC测量结果,“外壳”通常定义为散热器/冷板界面处的散热器中心点,这将是冷板上的最热点,但不一定是器件“外壳”上的最冷点。准确进行θ-JC 测量所面临的一个实际困难是要在不干扰热流的情况下进行测量。冷板表面的凹槽可能会显著减小界面面积;冷板上的钻孔也会干扰热流,不过如果孔足够小的话,影响可能不大。另一个问题是,当看不到外壳时,外壳测量热电偶与外壳的接触程度如何。或者,测量散热器暴露边缘(比如 Dpak 或 TO220的耳片上)的温度可以绕过上述两个困难,但它可能产生明显不同的结果(可能比“真实”θ-JC 值高 20-40%)。显然,要在实际应用环境中成功使用θ-JC 值,应用必须确保几乎 100%的器件功率流经外壳。
最后,冷板上测量的θ-JC 值可能与相应的“ψ-JC”值有很大不同,即使这两种测量的热电偶位置可能相同(参见以下关于“ψ”值的讨论)。这是因为,与冷板设置相比,在非冷板测试设置中经过“外壳”点的热量比例很可能要小得多。事实上,如果θ-JC 值是从 100%热条件得出的,那么对应的ψ-JC 值会较低,这是不言而喻的。例如,在非冷板安装情况下,如果只有 10%的热量流过“外壳”,那么ψ-JC 将是θ-JC 值的十分之一!
显然,θ-JA与θ-JC的区别在于,θ-JA必然包括整个系统,而不仅仅是封装,而θ-JC被理想化为“仅封装”特性。θ-JC 是θ-JA 的一小部分的说法并不罕见,它的意思是,在确定器件的工作结温时,外部环境的热设计比器件本身的热设计更重要。
数据表上出现的这些值的问题是,θ-JA 很可能不适用于客户的特定应用,因为封装外部的系统会有差异,例如气流条件、金属厚度、电路板面积和布局、相邻器件的接近程度和功耗等。因此,θ-JA 可能看似方便,因为您只需要知道环境温度,但实际上,除非应用与热测试情况完全相同,否则应使用不同的θ-JA,而且其差异可能相当大。数据表可能会显示“最小焊盘”值和“1 英寸焊盘”值或其中之一,但应用中的实际θ-JA 可能优于“1 英寸焊盘”值,或者可能劣于“最小焊盘”值。在任何情况下,如果系统不同,那么数据表中的θ-JA就不是真正有用的值。
θ-JC可能更有用,因为它可能真正描述了器件在实际应用中的特性,即便如此,只有当外部系统也得到全面定义时,它才是真正有用的。这里的问题是,不能简单地假设外壳温度可以控制为任意选择的值;更确切地说,外部散热系统的设计必须确保器件消耗的功率也是如此。例如,考虑一个特定的 TO264 功率晶体管,其θ-JC 为0.4°C/W。如果最大 Tj 为 150°C 且外壳温度可保持在 25°C,那么功耗原则上可以为 312.5 W [Pd = (TJ−TC) / θJC]。
然而,什么样的外部系统可以将外壳“保持”在 25°C 呢?一个能够吸收 400 W 的水冷冷板——其热阻约为0.2°C/W,从冷板上的安装点测量到“无限”供应的冷却剂——怎么样?要吸收 312.5 W,意味着冷却剂本身须保持在比外壳温度低0.2°C/W * 312.5 W = 62.5°C 的温度,也就是-37.5°C!事实上,这种 TO264 器件的一个实际应用可以利用强制风冷散热器,其表面积为 100平方英寸,净热阻为0.2°C/W(容量与刚才说明的水冷冷板非常相似)。但在这个实际系统中,是环境温度以 25°C 为限,而不是器件外壳温度。由于系统总热阻(θ-JA)为0.6°C/W(器件为0.4,加上散热器0.2),因此实际最大功耗为 208 W,稳态平衡时的外壳温度约为 66°C。
ψ 值与θ值相比,并不是真正的热阻,尽管它们具有相同的单位。JEDEC 将该术语定义为一个“热特性参数”1。它只不过是系统中两个选定点之间的温差与相关器件总功耗之比。定义它的公式与θ的公式基本相同,即:
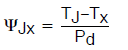
 (公式5)
(公式5)
并且
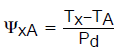
 (公式6)
(公式6)
注意
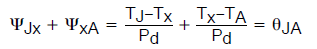
 (公式7)
(公式7)
请注意,我们定义了两个变体,一个指结至某一任意封装位置 x,另一个指该任意封装位置 x 至环境。这会让人误以为前者主要是“封装”特性,而后者主要是“环境”特性。但实际情况是,所选择的封装位置仅仅是任意地将整个系统θ-JA 分成两部分,保证其相加得到正确的总数(公式 7)。这并不说明,随着周围环境变化,两个端点之间的位置x将具有可预测的温度。只有环境不变时,它才是可预测的。(与此形成对比的是,θ-JC 始终会得出一个相对于结的可预测温度,而不管外壳之外的环境发生什么变化,至少在理想情况下是如此。)尽管如此,就像θ值一样,知道相应的输入后,可以根据下式预测工作温度:

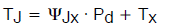 (公式8)
(公式8)
或
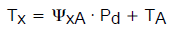 (公式9)
(公式9)
对于半导体器件和封装,常见数据表ψ值包括:ψ-JLn(指定特定引线 n)、ψ-JT(T 代表外壳顶部)、ψ-J-tab(tab 是合适功率器件上暴露的散热器耳片)和ψ-J-board(其中可能指定封装中心正下方的电路板,例如对于 BGA 型封装)。
通常可以知道相关器件的总功耗,但要知道通过外壳顶部流出的热量比例、通过引线流出的热量比例、通过封装下方的气隙流出的热量比例等等,要困难得多。尽管在整个封装的各种位置进行温度测量可能是可行的,但沿着选定路径进行实际的热流量测量是很困难的或不可能的。此外,这些路径在与结相关时的实际热阻及其对外部变化的敏感性方面可能大不相同。因此,随着安装条件的变化,沿各种可能路径的相对热流量可能会有显著偏移。所以,数据表上报告的ψ值只能是在已知热流量分布相似时,用于估计应用温度。关于有效应用ψ值的最低规定是,相同比例的热量沿着实验室测量过程中出现的特定ψ路径流动;一般来说,这很难确定,甚至不可能确定。
以2引线轴向器件为例。它是在具有对称布局的热测试板上测量的,到每条引线的走线金属量相等。在该测试场景中,θ-JA 为 45°C/W,ψ-JL 为 15°C/W(由于对称性,每条引线的值相同)2。现在,在一个特定应用中,该器件安装在一个电路板上,其 1 平方英寸焊盘仅分配给两条引线中的一条;另一条引线具有最小走线。在该应用板上进行的测量得到的θ-JA 现在为 31°C/W,并且ψ-JL1 = 21°C/W,ψ-JL2 = 9°C/W,极不对称。应该清楚的是,如果使用数据表的ψ-JL 值来预测结温,可能会产生极高或极低的值,具体取决于要使用哪条引线温度作为参考点。如果回到真正热阻的概念,可以看出,在最初的实验室测量中,真正θ-JL 值应为 30°C/W,因为每条引线承载恰好一半的总功率。
2遗憾的是,在这个特定例子中,数据表是 1995 年以前编写的,将该值称为“结至引线热阻”,但没有解释如何应用该值。它是一个ψ值还是一个θ值?绝对不是结果计算中很小的二比一差异!
也就是说
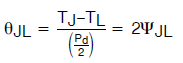 (公式10)
(公式10)
事实上,知道该θ值后就可以在任何应用环境中精确预测结温,无论散热金属的布置有多么不对称,只要测量两个引线温度而不是仅仅依赖一个温度,具体而言:

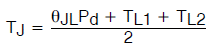 (公式11)
(公式11)
可以使用公式 10将此表达式整理成下式:
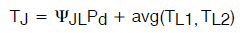
 (公式12)
(公式12)
因此,在这一特定的双引线器件示例中,可以看出,如果在实际应用中测量两个引线温度,则甚至ψ-JL 也可加以利用。然而,在更复杂的封装情况下,可能会有多条引线,其中一些直接连接到内部“标志”,而另一些则不是,或者可能存在其他明显不对称的热路径。然后,改变与各条引线相关的金属走线面积的量,或者在暴露的外壳上增加外部散热器,可能会显著改变相对热流,并因此使得公布的ψ值完全无效。通常,当为数据表选择要进行表征的引线时,如果能够确定承载功率比例最大的引线,那么最好选择该引线。这很可能是ψ-JL 最大的引线,特别是如果它在内部直接连接到标志,并且在外部有一个不成比例的大散热器。这样的值对于实际应用环境的适度变化是最不敏感的。另一方面,如果数据表指定一条已知不具有最大热流量的引线,那么我们就无法确定在特定应用中,实际ψ值是高于还是低于数据表中提供的值。
多结器件和矩阵公式
提到多结器件时,我们一般指的是包含相对独立的多个电气元件的器件,其各种可能的“结”的功耗比例可能相差很大。它可以是一个模拟器件,有两路不同的稳压输出,驱动大不相同的负载。它可以是一个双整流器封装,在一种应用中相当平等地利用两个通道,但在另一种应用中,可能优先利用其中一个通道。它可以是一个单一应用,不时地在两个完全不同的工作点之间移动;需要确定哪种情况是“最坏情况”。只要考虑的是恒定功率条件,那么利用稳态值的矩阵方法就是一种描述系统热特性的简明方法。它依赖于线性叠加原理,即系统中任何给定点的温升是系统中每个热源的可独立导出的温升之和。以矩阵形式表示就是:

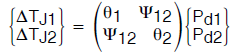 (公式13)
(公式13)
请注意,矩阵表示法只是如下一对方程的简写版本:

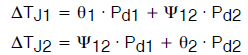 (公式14)
(公式14)
对于双结器件,这意味着第一个结的温升是其“自发热”特性乘以其自身功耗与“相互作用”特性乘以另一个结的功耗之和。适用于线性系统的另一个原理是互易,根据该原理可知,一个结加热另一个结的量等于它被另一个结加热的量,因此该矩阵具有关于主对角线的对称性。
注意,这里我们用ψ表示相互作用项。这是严格正确的,因为一般而言,我们不能说任一结耗散的热量的特定部分“经过”另一个结;其中一些肯定是这样流动的,导致那里的温度上升。另一方面,自发热项使用了θ。这不是严格正确的,除非我们有前面讨论中就θ值提出的保证,即θ所指的参考点是两个结所消耗的 100%功率的最终目的地。然而,如上所示,如果需要多个参考温度的话,即使基本矩阵公式本身也是对所需数学描述的过度简化。
简单地说,对于理想化的简单情况,矩阵公式通常由θ-JA 自发热值和ψ-JA 相互作用加热值组成,或者可能由θ-JB 值和ψ-JB 值组成;封装中心的电路板位置经确定后,假定它代表主要热流路径和公共参考温度。这种简单矩阵方法在一些情况下有效,描述这些情况的一种方法是:只要有单一温度边界条件,该公式就适用。但在使用ψ参数表征引线、电路板或外壳顶部温度的典型情况下,这些额外的温度位置不是真正的边界条件,而是测量但不控制温度的辅助参考点。
即使有这种限制,也应注意,矩阵描述很容易扩展到任何数量的结和辅助温度,每个相关的热源对于每个其他结和相关的点都产生一个自加热θ和一组相互作用ψ。例如,假设有三个热源、一条引线和一个电路板温度参考位置,那么我们将有:

 (公式15)
(公式15)
这里不是方阵,因为我们使用ψ特性来描述系统中某些点的温度,这些点本身不是热源。也许很明显,互易定理带来的对称性只适用于仅代表热源温度的方形子矩阵。同样,前面的矩阵表示法只是如下方程组的简写版本:

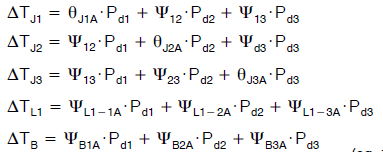 (公式16)
(公式16)
对所有结果必须加上环境温度。
在实践中,通常测量三个功率水平和三个温度(引线、电路板和环境温度)。然后,利用矩阵方法可以计算五个温度:三个结温以及引线和电路板的温度。如果计算温度与测量值一致,那么您就可以在一定程度上相信,所有特性输入(θ和ψ)对所考虑的系统都是有效的。如果引线和电路板的计算值与测量值之间存在显著差异,您就可以得知,实际应用中的热流分布与最初推导ψ时的热流分布显著不同,因而计算的结温也值得怀疑。
为了完整起见,我们将展示真正的多热源、多温度边界条件模型所需的额外复杂性。假设有一个六引线封装,其内部有两个独立的硅器件。如果我们可以对所有六条引线进行温度测量,假设内部产生的热量几乎 100%必须沿着其中一条引线离开封装,那么我们可以写出以下矩阵方程,其中每条引线被视为一个单独的边界条件:
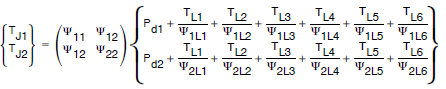
 (公式17)
(公式17)
这个完整模型与以前较简单的矩阵公式之间存在两个重要区别。首先,方程的左边是实际结温预测,不是超过某一公共参考温度的温升。其次,温度边界条件显示为准热量输入。每一个都有自己相关的权重,在这里表示为另一个ψ值。因此,虽然只有两个热源,但实际上有 16 个不同参数来表征这个模型。显然,说这样的模型可能存在是一回事,通过实验推导出所有这些系数则完全是另一回事。这属于“紧凑模型”领域,在过去十年中,该领域产生了大量文献和研究。达到一定精度所需的独立外部边界条件的最小数量,是否必须考虑温度非线性,甚至模型的内部结构,都是充分发展这种模型所必须解决的重要问题。
θ-JA与铜面积的关系
提供制造商热特性数据的最大问题之一,在于选择何数据有助于说明,但遗憾的是,该数据可能会严重歪曲封装在客户应用中的实际表现。一个很好的例子是θ-JA 随铜面积的变化,如下图所示。
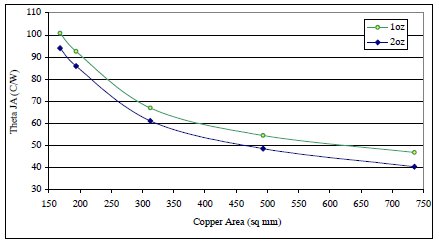
图1. Dpak的θ-JA与铜面积的关系
此图中明示的两个参数是散热铜的厚度(两种代表性厚度,每种厚度一条曲线)和铜面积(x 轴)。即使只考虑这两项,也会出现许多问题。例如,如果铜的厚度超出了所提供的范围,应该怎么办?事实上,即使在所提供的范围内,是否应该以线性方式进行解读?如果铜面积低于所提供曲线的左端或高于右端,会发生什么情况?线性外推合适吗?曲线是否应该拟合已知的点,并进行扩展(如果是,多远是合适的)?金属面积是否包括与目标器件直接相关的走线?如果包括,很明显,在这些曲线左端的某一点,面积会从大的“块状”面积过渡到细长的面积。在这种过渡中,散热能力肯定会发生显著变化。因此,如果特定应用中使用的纯“走线”金属的量与此图所基于的量不同,将会出现与“直观”外推有显著偏差的情况。
然而,除了这些明示的参数之外,还有许多非常重要的因素未在此图上明示,它们会影响实际的θ-JA 值。例如,铜面积之外的电路板有多大?气流有多大?电路板顶部和底部的气流是否相同?如果空气是“静止的”,电路板相对于重力的方向是什么,它如何随方向而变化?
要点是,这些图表只能用于非常粗浅地了解目标器件可以在多大程度上被利用来调节系统整体热特性。显然,起始点是减去器件“固有”特性(如ψ-J-lead),看看剩下的特性是否有足够的裕量来提供所需的补偿。如果有,则必须对外部热系统进行全面分析,至少要考虑上述讨论中强调的所有变量。
点个星标,茫茫人海也能一眼看到我

原文标题:封装设计解惑:如何使用数据表中的稳态热特性参数
文章出处:【微信公众号:安森美】欢迎添加关注!文章转载请注明出处。
-
安森美
+关注
关注
32文章
1685浏览量
92039
原文标题:封装设计解惑:如何使用数据表中的稳态热特性参数
文章出处:【微信号:onsemi-china,微信公众号:安森美】欢迎添加关注!文章转载请注明出处。
发布评论请先 登录
相关推荐
在ADS4142的数据表第18页, 表4中,tSU和tH是怎么定义的?
opa1622 TINA仿真模型相位结果与数据表中不符是怎么回事?
请问LM397数据表中“input over drive” 是什么意思?
如何降低输入引起的稳态误差
SN54LS375、SN74LS375双稳态锁存器数据表

具有SCHMITT-TRIGGER输入的双单稳态多谐振荡器数据表

CMOS双精度单稳态多谐振荡器CD14538B TYPES 数据表

CMOS双单稳态多谐振荡器CD4098B Types数据表

带开关量输入的单稳态多谐振荡器SN54121 SN74121数据表





 封装设计解惑:如何使用数据表中的稳态热特性参数
封装设计解惑:如何使用数据表中的稳态热特性参数










评论