任何信号链设计的基本挑战之一是确保系统本底噪声足够低,以便模数转换器 (ADC) 解析感兴趣的信号。无论您如何努力最大限度地降低功耗、减少电路板空间或降低成本,大于输入信号的噪声水平都会使任何设计变得毫无用处。因此,任何模拟设计人员都必须了解信号链噪声、其对模数转换的影响以及如何将其影响降至最低,这是任何模拟设计人员的基础知识。
为此,本“解析信号”系列旨在全面了解 Δ-Σ ADC 中的噪声。在这些文章中,我将研究典型信号链中的常见噪声源,并通过减轻噪声和保持高精度测量的方法来补充这种理解。
在继续之前,重要的是要注意,本系列文章涵盖精度(噪声),而不是准确性。虽然这两个术语经常互换使用,但它们指的是信号链设计的不同(尽管相关)方面。在设计高性能数据采集系统时,除了尽量减少噪声之外,您还必须考虑不准确引起的误差,例如偏移、增益误差、积分非线性 (INL) 和漂移。
在本系列的第 1 部分中,我将重点介绍 ADC 噪声基础知识,同时回答问题和讨论以下主题:
- 什么是噪音?
- 典型信号链中的噪声来自哪里?
- 了解 ADC 中的固有噪声。
- 高分辨率与低分辨率 ADC 中的噪声有何不同?
在第 2 部分中,我会将重点转移到以下主题上:
在第 3 部分中,我将逐步介绍一个使用电阻桥的完整设计示例,以帮助说明第 1 部分和第 2 部分中的理论如何应用于实际应用。
什么是噪音?它来自哪里?
噪声是任何不需要的信号(通常是随机的),它添加到所需信号中,导致其偏离其原始值。噪声是所有电气系统固有的,因此不存在“无噪声”电路之类的东西。
图 1 描述了您在现实世界中可能会如何体验噪声:过滤掉噪声的图像和未过滤的相同图像。请注意图 1 左侧图像中清晰的细节,而右侧图像几乎完全模糊。在模数转换过程中,结果将是模拟输入和数字输出之间的信息丢失,就像图 1 中的两个图像几乎没有相似之处一样。

图 1:无噪声图像(左);带有噪声的相同图像(右)
在电子电路中,噪声有多种形式,包括:
- 宽带(热、约翰逊)噪声,它是由电导体内电荷的物理运动引起的与温度相关的噪声。
- 1/f(粉红色,闪烁)噪声,是功率密度与频率成反比的低频噪声。
- 爆米花(爆裂)噪声,这种噪声本质上是低频的,由设备缺陷引起,使其具有随机性且在数学上不可预测。
这些形式的噪声可能通过多种来源进入信号链,包括:
- ADC,它会产生热噪声和量化噪声的组合。
- 内部或外部放大器,可以添加 ADC 然后采样的宽带和 1/f 噪声,从而影响输出代码结果。
- 内部或外部参考电压,也会产生出现在 ADC 输出代码中的宽带和 1/f 噪声。
- 非理想电源,可能会在您尝试通过多种耦合方式测量的信号中添加噪声。
- 内部或外部时钟会产生抖动,从而导致采样不均匀。这对于正弦输入信号来说是一个额外的噪声源,通常对于高速 ADC 更为重要。
- 印刷电路板 (PCB) 布局不佳,可能会将来自系统其他部分或环境的噪声耦合到敏感的模拟电路中。
- 传感器,它可能是高分辨率系统中噪音最大的组件之一。
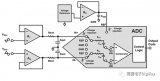
图 2 描绘了典型信号链中的这些噪声源。

图 2. 典型供应链中的常见噪声源
在这个由 9 部分组成的系列的第 1-3 部分中,我将只关注固有的 ADC 噪声。为了更全面地理解,我将在单独的文章中讨论其余电路组件中的噪声源。
ADC 中的固有噪声
您可以将总 ADC 噪声分为两个主要来源:量化噪声和热噪声。这两个噪声源是不相关的,这使得总和平方根 (RSS) 方法能够确定总 ADC 噪声 NADC Total,如公式 1 所示:

每个 ADC 噪声源都有特定的特性,这些特性对于了解如何减轻固有的 ADC 噪声很重要。
量化噪声
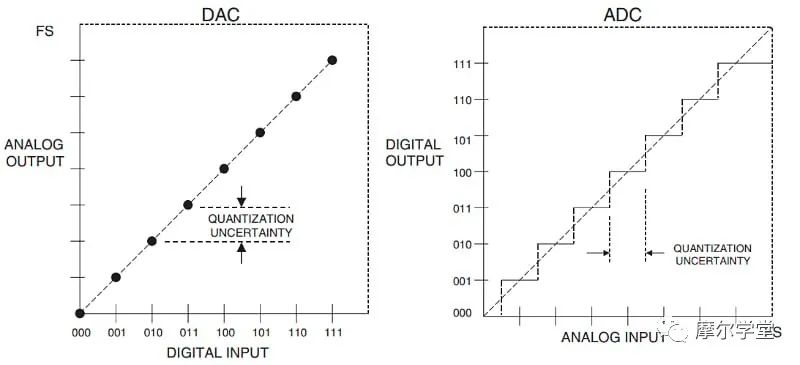
图 3 描绘了 ADC 的理想传递函数图(不受偏移或增益误差的影响)。传递函数从最小输入电压水平延伸到最大输入电压,并根据沿垂直轴的 ADC 代码总数分为多个步骤。这个特殊的图有 16 个代码或步骤,代表一个 4 位 ADC。(注意:使用直接二进制代码的 ADC 将具有仅包含第一象限的传递函数。)

图 3. ADC 的理想传递函数
量化噪声来自将无限数量的模拟电压映射到有限数量的数字代码的过程。因此,任何单个数字输出都可以对应多个模拟输入电压,这些电压可能相差 1/2 最低有效位 (LSB),这在公式 2 中定义:

其中 FSR 表示以伏特为单位的满量程范围的值,N 是 ADC 的分辨率。
如果将此 LSB 误差相对于量化的 AC 信号进行映射,则会得到如图 4 所示的图。请注意量化的“阶梯”形数字输出与平滑的正弦模拟输入之间的不同之处. 取这两个波形之间的差异并绘制结果,会产生如图 4 底部所示的“锯齿”形误差。该误差在 ±½ LSB 之间变化,并在结果中表现为噪声。
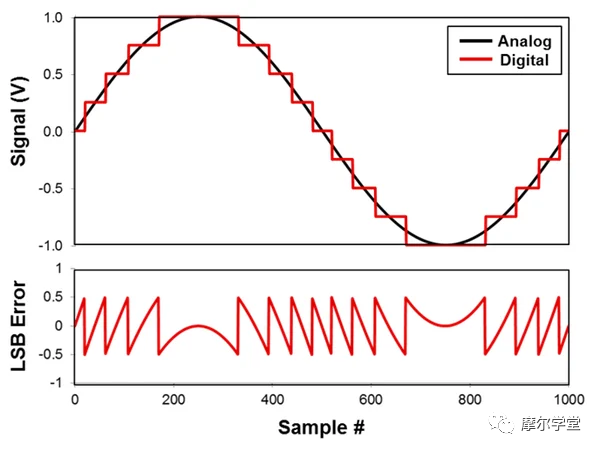
图 4. 模拟输入、数字输出和 LSB 误差波形
类似地,对于 DC 信号,与量化相关的误差在输入信号的 ±½ LSB 之间变化。然而,由于 DC 信号没有频率成分,量化“噪声”实际上表现为 ADC 输出中的偏移误差。
最后,量化噪声的一个明显但重要的结果是 ADC 无法进行超出其分辨率的测量,因为它无法区分输入中的 sub-LSB 变化。
热噪声
与作为模数(或数模)转换过程的副产品的量化噪声不同,热噪声是所有电子元件中固有的一种现象,是电导体内电荷物理运动的结果。因此,即使不施加输入信号,您也可以测量热噪声。
不幸的是,ADC 最终用户无法影响器件的热噪声,因为它是 ADC 设计的函数。在本文的其余部分,我将量化噪声以外的所有 ADC 噪声源称为 ADC 的热噪声。
图 5 描绘了时域中的热噪声,它通常具有高斯分布。
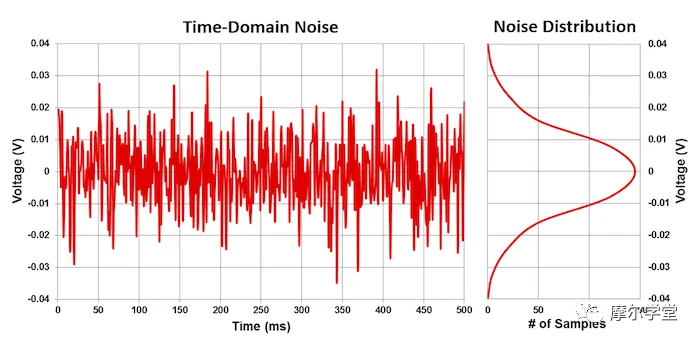
图 5. 高斯分布时域中的热噪声
尽管您无法影响 ADC 的固有热噪声,但由于其依赖于 LSB 大小,您可能会改变 ADC 的量化噪声水平。但是,量化这种变化的重要性取决于您使用的是“高分辨率”还是“低分辨率”ADC。让我们快速定义这两个术语,以便您可以更好地了解如何利用 LSB 大小和量化噪声为您带来优势。
高分辨率与低分辨率 ADC
低分辨率 ADC 是总噪声更依赖于量化噪声的任何设备,例如 NADC,Quantization >> NADC,Thermal。相反,高分辨率 ADC 是总噪声更依赖于热噪声的任何设备,例如 NADC,Quantization << NADC,Thermal。低分辨率和高分辨率之间的转换通常发生在 16 位级别,任何大于 16 位的都被认为是高分辨率,而任何小于 16 位的都被认为是低分辨率。虽然并非总是如此,但我将在本系列的其余部分保持这一一般惯例。
为什么要在 16 位级别进行这种区分?让我们查看两个 ADC 数据表以找出答案。图 6 显示了德州仪器 (TI) 的 ADS114S08、16 位 delta-sigma ADC 及其 24 位对应产品 ADS124S08 的实际噪声表。除了分辨率之外,这些 ADC 是相同的。
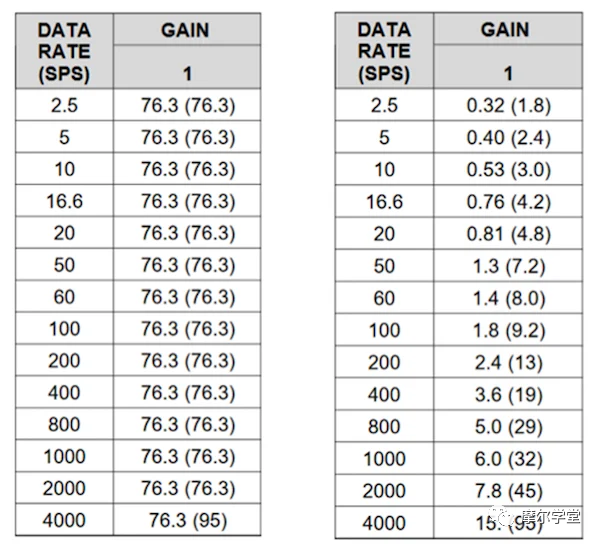
图 6. 16 位 ADS114S08(左)和 24 位 ADS124S08(右)的输入参考噪声,单位为 µV RMS (µV PP ),V REF = 2.5V,G = 1V/V
在 16 位 ADS114S08 的噪声表中,无论数据速率如何,所有以输入为参考的噪声电压都是相同的。将其与 24 位 ADS124S08 的输入参考噪声值进行比较,这些值都不同并且随着数据速率的降低而降低/提高。
虽然这本身不会导致任何明确的结论,但让我们使用公式 3 和 4 来计算每个 ADC 的 LSB 大小,假设参考电压为 2.5V:

结合这些观察结果,您可以看到数据表中报告的低分辨率(16 位)ADC 的噪声性能相当于其 LSB 大小(最大量化噪声)。另一方面,高分辨率(24 位)ADC 数据手册中报告的噪声显然远大于其 LSB 大小(量化噪声)。在这种情况下,高分辨率 ADC 的量化噪声非常低,可以有效地被热噪声隐藏。下面的图 7 定性地表示了这种比较。
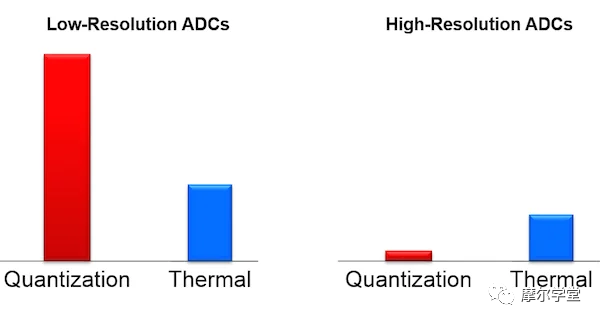
图 7. 低分辨率(左)和高分辨率(右)ADC 中量化噪声和热噪声的定性表示
你如何利用这个结果来发挥你的优势?对于量化噪声占主导地位的低分辨率 ADC,使用较小的参考电压来减小 LSB 大小,从而降低量化噪声幅度。这具有降低 ADC 总噪声的效果,如图 8(左)所示。
对于热噪声占主导地位的高分辨率 ADC,使用更大的参考电压来增加 ADC 的输入范围(动态范围),同时确保量化噪声水平保持在热噪声以下。假设没有其他系统变化,这种增加的参考电压可实现更好的信噪比,如图 8(右)所示。

图 8. 调整低分辨率(左)和高分辨率(右)ADC 中的量化噪声以提高性能
现在您了解了 ADC 噪声的组成以及它们在高分辨率和低分辨率 ADC 之间的差异,您可以将这些知识用于第 2 部分,我将在该部分讨论如何在 ADC 的数据表中测量和指定噪声。
总结要点
以下是有助于更好地理解 delta-sigma ADC 中噪声的要点摘要:
- 噪声是所有电气系统固有的。
- 噪声是通过所有信号链组件引入的。
- ADC 噪声有两种主要类型:
- 量化噪声,与参考电压成比例。
- 热噪声,这是给定 ADC 的固定值。
- 一种类型的噪声通常占主导地位,具体取决于 ADC 的分辨率:
- 量化噪声控制。
- 分辨率通常受 LSB 大小限制。
- 降低参考电压以降低量化噪声并提高分辨率。
- 热噪声为主。
- 分辨率通常 >1 LSB。
- 增加参考电压以增加动态范围。
- 高分辨率ADC特性:
- 低分辨率ADC特性:
-
电路板
+关注
关注
140文章
4963浏览量
97985 -
噪声
+关注
关注
13文章
1122浏览量
47428 -
模数转换器
+关注
关注
26文章
3206浏览量
126856
发布评论请先 登录
相关推荐
有ADC和传感器的基础知识吗?
WiFi基础知识解析
STM32H7的ADC基础知识和HAL库API
ADC转换器的基础知识详细资料说明
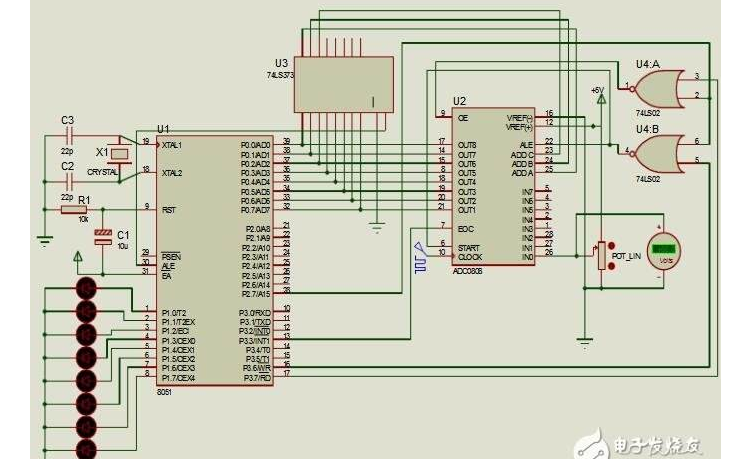
模拟基础知识:处理SAR ADC输入驱动难题




 浅析ADC噪声基础知识
浅析ADC噪声基础知识











评论