PID控制算法详解(三)

各个环节的特点:

比例作用：输出与输入曲线相似;

积分作用：只要输入有偏差输出就变化;

微分作用：输入有抖动输出才有变化，且会猛烈变化。

01对微分的理解

系统的输出量与输入量对时间的微分成正比，即输出量反映输入量的变化率，而不反映输入量本身的大小。因此，可由微分环节的输出来反映输入信号的变化趋势，加快系统控制作用实现。所以常用微分环节来改善系统的动态响应。

微分的作用能够超前调节，单纯的微分作用是不存在的，同积分作用一样。

1.微分作用与被调量的大小无关，但与被调量的变化速率有关;

2.微分参数一般只有一个，用微分时间表示。有些有两个：微分增益与微分时间。但是我们一般只调节微分增益。微分增益表示输出波动的幅度，波动后还要输出回归，微分时间表示回归的快慢。从下图可以稍微理解一下：

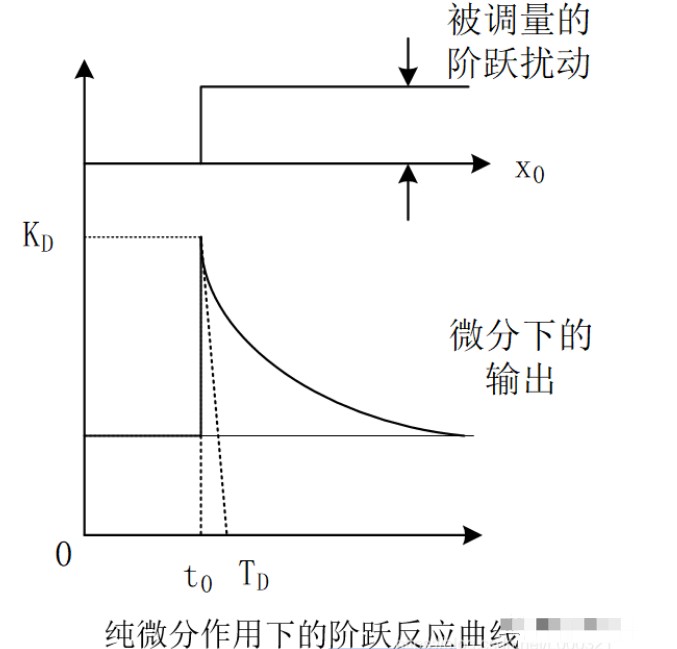
02微分适用范围

对于微分项的适用，不是所有的系统都适用。很多人常常会将比例积分微分一起用于系统的控制。比例积分可以都适用，但是有些系统用微分是不恰当的。

1.被调量很难稳定在一个数值，微分作用会因为被调量的小波动，使得输出大幅度来回动作，形成干扰，而且对执行机构也不利。就如被调量是水位、气压、风压的调节系统不适合使用微分。他们本身的数值容易受各种因素影响，即使稳定的系统，被调量也很难稳定在一个数值。就如我现在研究生学习阶段的方向是永磁同步电机的控制，在采用PID控制时，一般不引入微分控制;

2.被调量有微小扰动时，要先消除扰动再使用微分;

3.系统大延迟的情况下应使用微分。

03仿真实验分析

搭建PID控制器如图所示，为保证仿真的有效性，仿真的控制对象与采用Pi控制的参数与对象均为一阶惯性函数。微分增益一般取很小的值，初步取值为0.1。

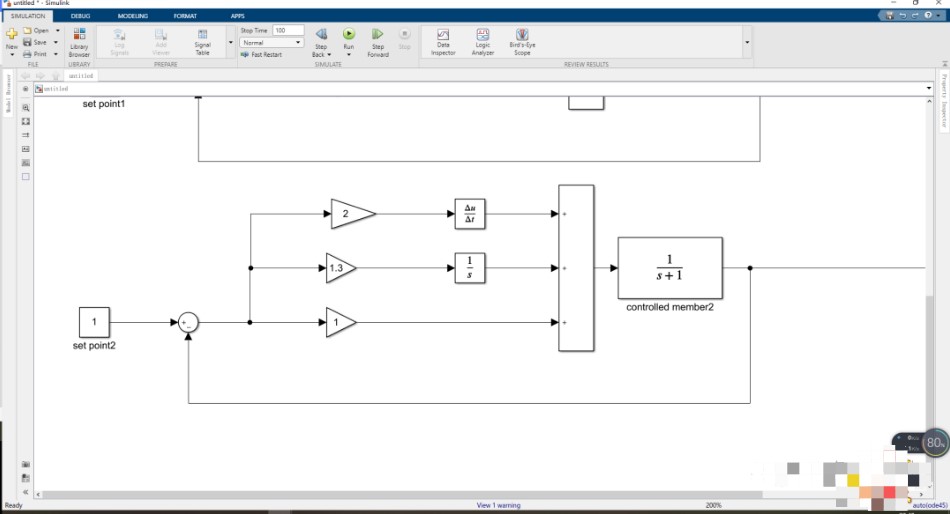
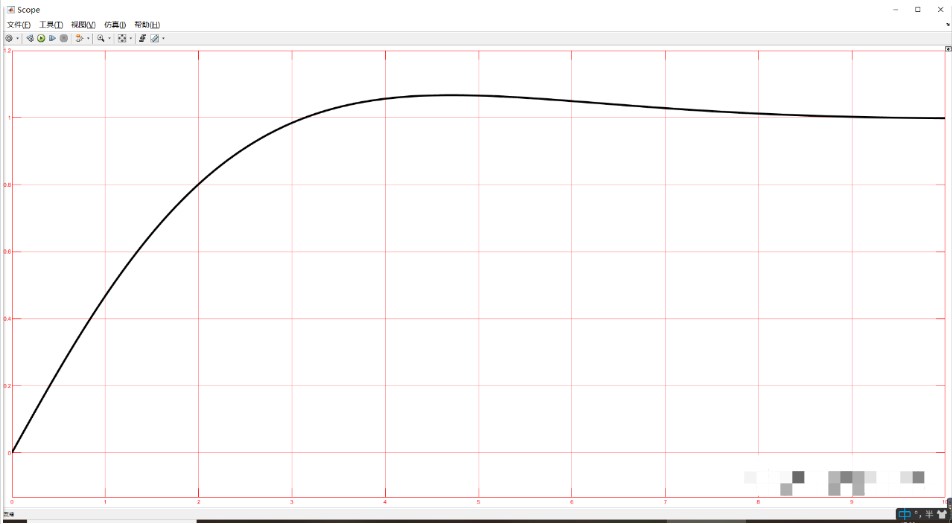
可以从仿真看出，输出逐步趋于期望值最后并稳定于1。闭环传递函数为：

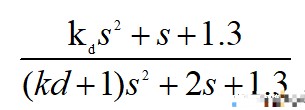
化为一般式：

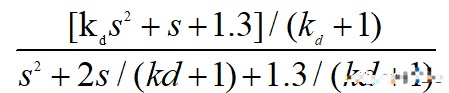
当s趋于0，即时间趋于无穷大时，其输出为1。

(从时域分析)要让系统响应无震荡和超调，那就要让系统处于一个临界阻尼状态。欠阻尼状态理解为系统的最佳状态，即ε要在[0,1]之间取值，二阶系统在欠阻尼时的响应为衰减震荡的，所以必然存在超调。从书本上了解到对于一个二阶系统在单位阶跃输入信号作用下的传递函数为：

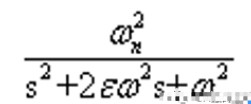
对于当前的仿真系统而言，其ki的计算值应该小于零。但是参数一般不可以是负数。大回路已经有负反馈了,再有负参数,成正反馈了,系统会不稳定。这个时候自己的理解就是不到万不得以，尽量不使用微分项，实在是太难调了。

04总结

1.微分项不到万不得已还是不要用了，头痛!微分项不适用任何系统，要根据系统的特性来使用，不然会适得其反;

2. 微分作用：输入有抖动输出才有变化，且会猛烈变化。微分就是提前预测控制;

3.当系统出现震荡时，可能不单单只与某一项参数有关，一定要仔细判断震荡曲线的特性，分辨出是哪个因素造成的，然后对症下药才能抑制震荡。