LTI连续系统的响应
连续系统的描述:电路图建立微分方程
1.数学模型
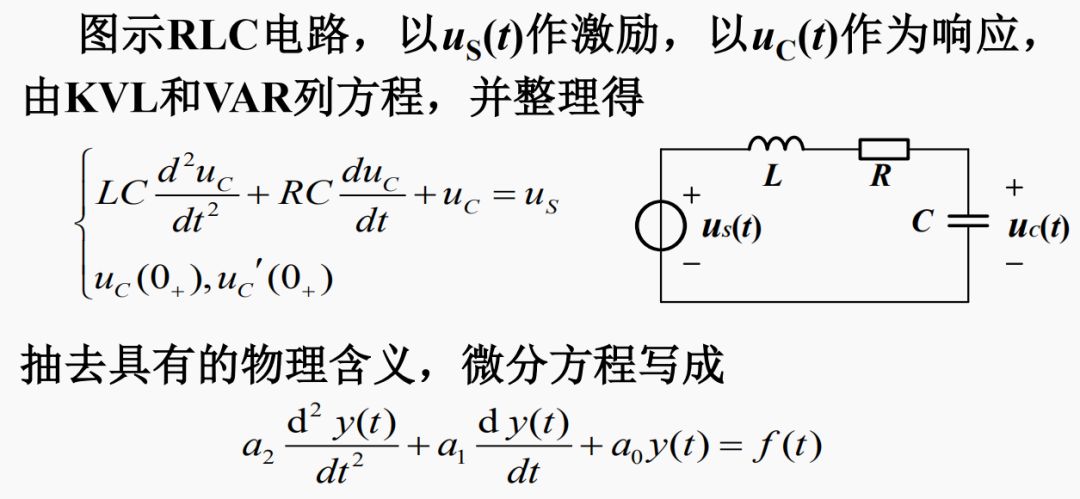
二阶常系数线性微分方程
2.相似系统
相似系统:能用相同方程描述的系统

微分方程的模拟框图
基本部件:
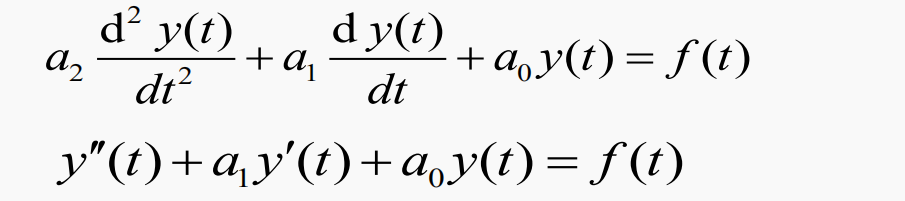
基本运算:数乘、微分、相加
基本部件:加法器、数乘器、积分器
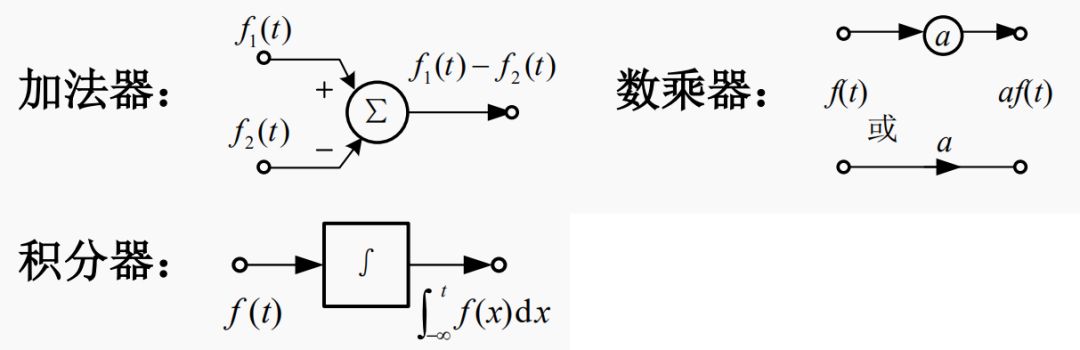
积分器的抗干扰性比微分器好(用积分器代替微分器)
2.模拟框图
模拟框图:将微分方程用基本部件的相互联接表征出来的图,简称框图。
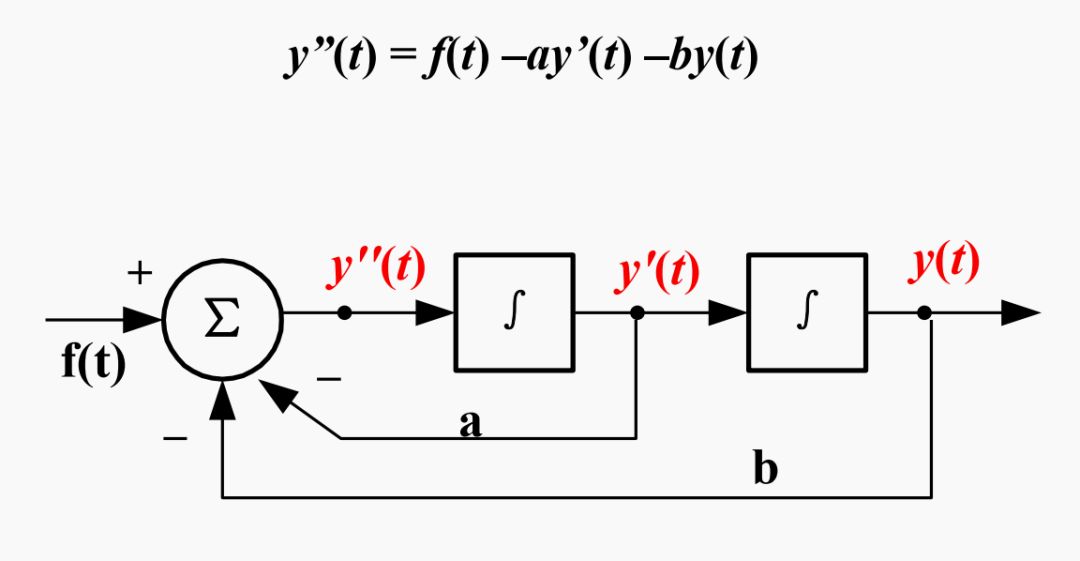
例1 已知y’’(t) + ay’(t)+ by(t) = f(t),画出框图。
解:将方程改写为 y”(t) = f(t) –ay’(t) –by(t)
绘制步骤为:
(1)画出两个积分器;
(2)以最后一个积分器的输出端为y(t);
(3)左边第一个积分器的输入端就是y”(t),也是加法器的输出。
例2 已知y“(t) + 3y'(t)+ 2y(t) = 4f'(t) + f(t),画框图。
解:该方程右端含f(t)的导数,引入辅助函数画出框图。 设辅助函数x(t)满足
x“(t) + 3x'(t)+ 2x(t) = f(t)
移项整理得: x”(t) = -3x’(t)-2x(t) + f(t)
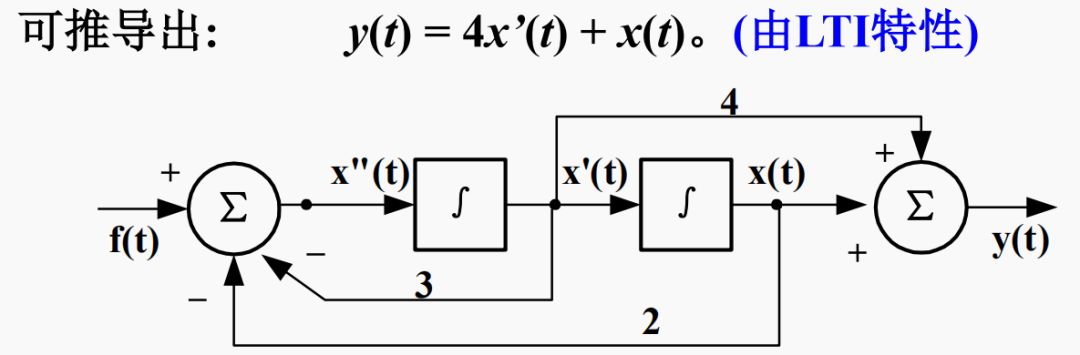
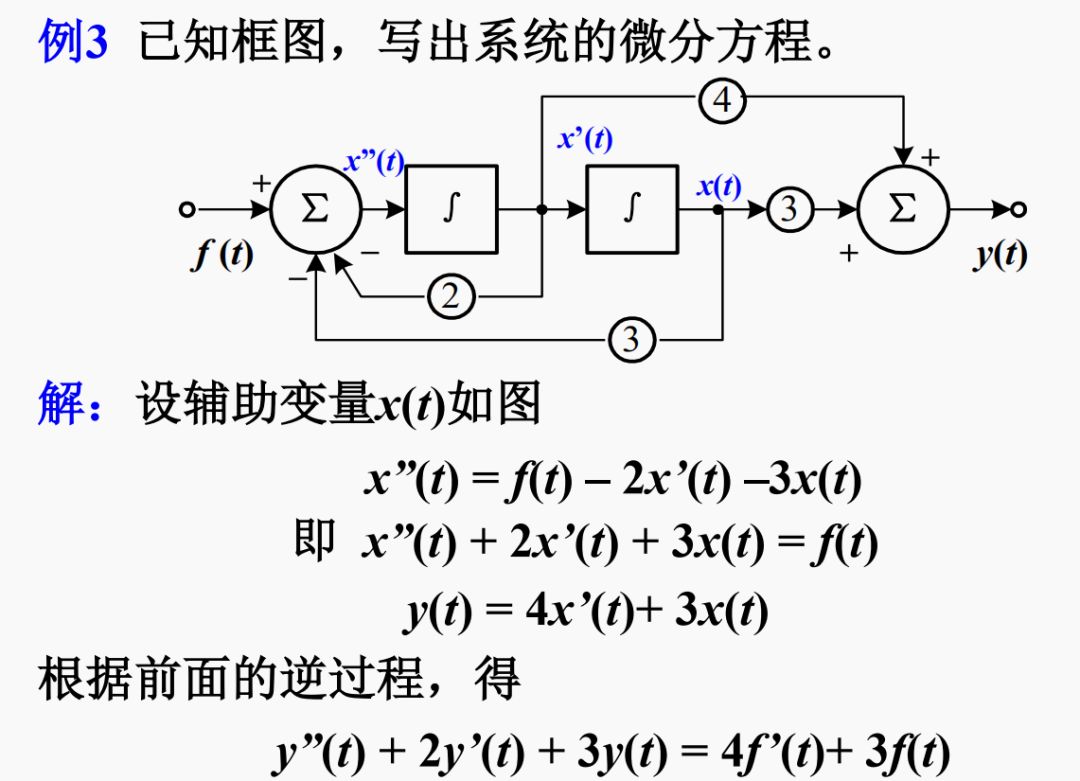
根据求和器列方程
微分方程的经典解法
经典解
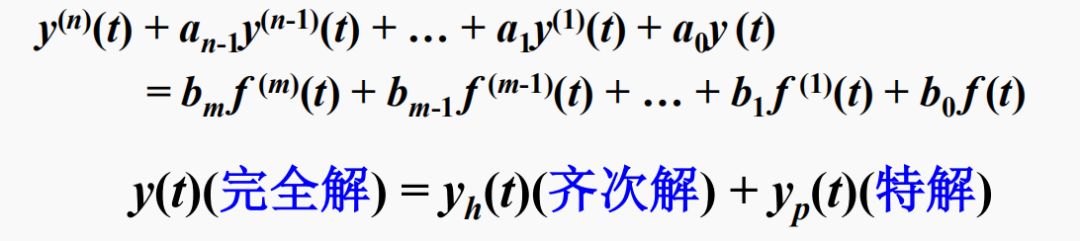
齐次解是对应齐次微分方程的解:
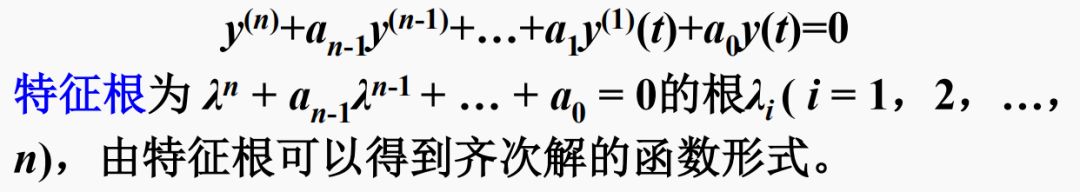
特解的函数形式与激励的函数形式有关。
2.齐次解的常用函数形式
不同特征根所对应的齐次解
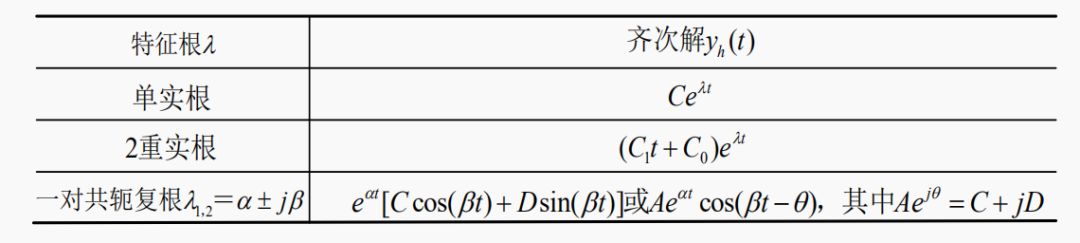
3.特解的常用函数形式
不同激励所对应的特解
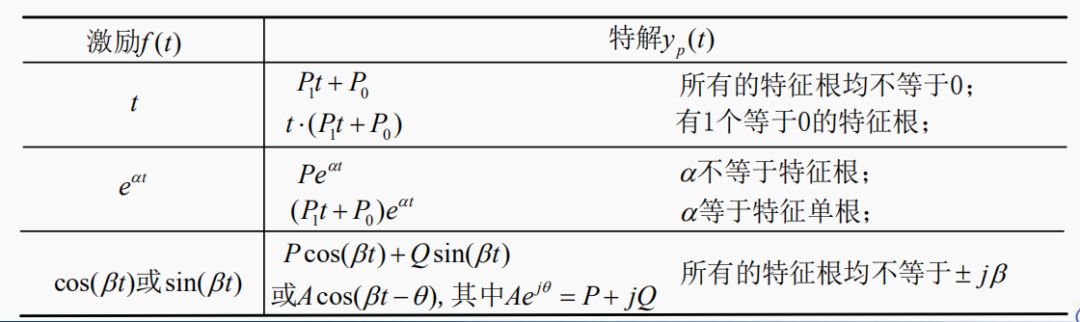


上式第一项系数C1 + Q0= 2,不能区分C1和Q0。
连续系统的初始值



结论:微分方程等号右端含有δ(t)时,仅在等号左端y(t)的最高阶导数中含有δ(t),则y(t)的次高阶跃变,其余连续; 若右端不含冲激函数,则不会跃变。
零输入响应

求解步骤
(1)设定齐次解;
(2)代入初始值,求待定系数

零状态响应

求解步骤
(1)设定齐次解;
(2)设定特解,代入方程求解;
(3)代入初始值,求待定系数。


响应分类
固有响应和强迫响应
固有响应仅与系统本身的特性有关,而与激励的函数形式无关。
齐次解的函数形式仅与特征方程的根有关,特征方程的根称为系统的“固有频率”,齐次解常称为系统的固有响应或自由响应。
强迫响应与激励的函数形式有关。
特解的函数形式与激励的函数形式有关,常称为强迫响应。
暂态响应和稳态响应
暂态响应是指响应中暂时出现的分量,随着时间的增长,它将消失。
稳态响应是稳定的分量,若存在,通常表现为阶跃函数和周期函数。 比如,电路系统中的直流稳态响应和正弦稳态响应。


Matlab求解系统的响应
求LTI系统的零状态响应的函数lsim,其调用格式为:
y=lsim(sys, f, t)
式中,t表示计算系统响应的抽样点向量; f是系统输入信号,sys是LTI系统模型,用来表示微分方程。
系统模型sys要借助tf函数获得,其调用方式为:
sys=tf(b, a)
式中,b和a分别为微分方程的右端和左端各项的系数。 比如:
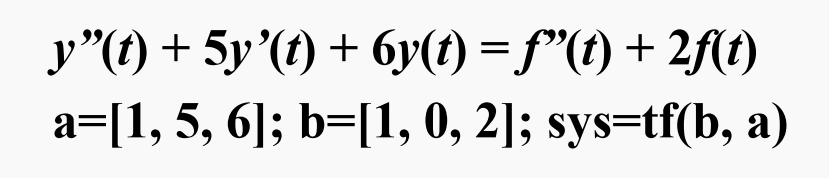
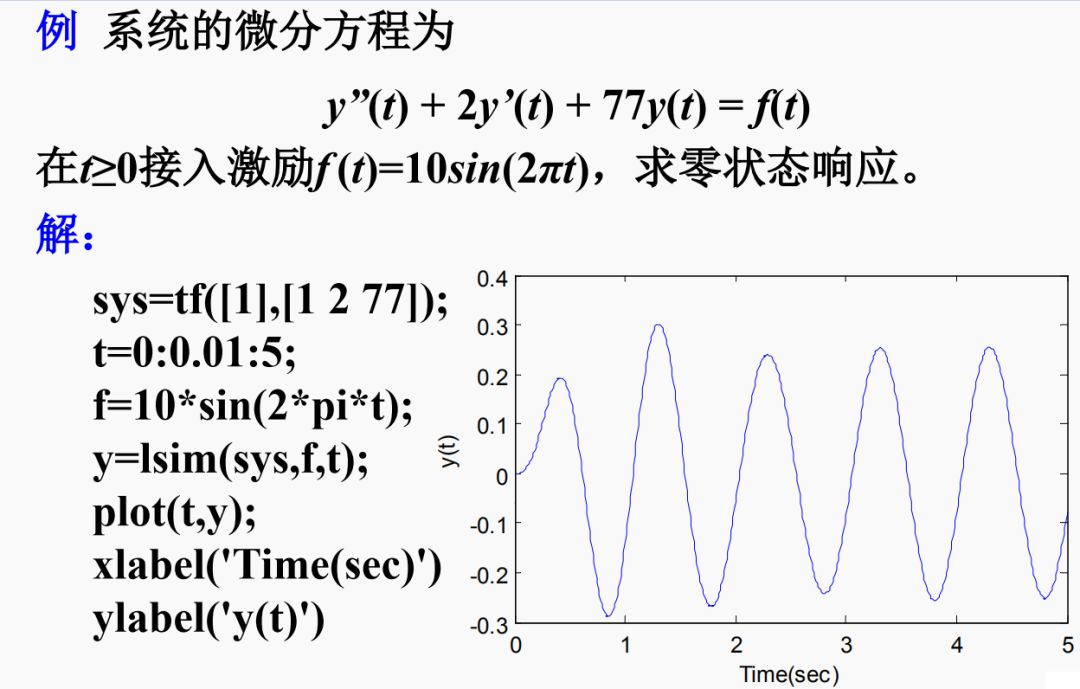
-
电路图
+关注
关注
10356文章
10725浏览量
532661 -
响应
+关注
关注
0文章
18浏览量
10851 -
数学模型
+关注
关注
0文章
83浏览量
11978 -
LTI
+关注
关注
0文章
11浏览量
10503 -
连续系统
+关注
关注
0文章
4浏览量
6763
发布评论请先 登录
相关推荐



连续时间LTI系统状态方程的求解
AMBA LTI协议规范
连续信号与系统的频域分析资料和方法,信号与系统三电子课件免费下载
LTI系统的单位阶跃响应详细资料说明





 LTI连续系统的响应
LTI连续系统的响应










评论