2.2 判别器:有问题?GAN来了!
GAN由生成器G和判别器D组成。
其实上面我们已经基本介绍了生成器G的由来了,并且我们遇到了一个问题: 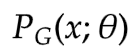 极其复杂的计算方式导致使用极大似然估计根本无从下手啊!!!
极其复杂的计算方式导致使用极大似然估计根本无从下手啊!!!
为了解决这个问题,我们引入了判别器D!
现在GAN的结构就完备了!!
对于生成器G:
-
G 是一个函数,输入
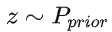 ,输出(上面已经介绍了)
,输出(上面已经介绍了)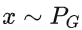
-
先验分布
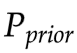 ,
, 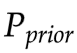 和G共同决定的分布
和G共同决定的分布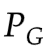
对于判别器D:
- D是一个函数,输入
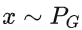 ,输出一个scalar
,输出一个scalar - D用于评估
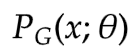 和
和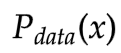 之间的差异(解决上一小节提出的问题)
之间的差异(解决上一小节提出的问题)
那么,GAN的最终目标-->用符号化语言表示就是:

我们的目标是得到使得式子 最小的生成器
最小的生成器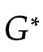 .
.
关于V:
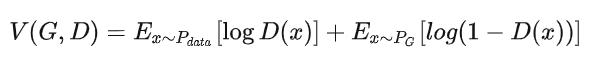
给定G,
衡量的就是分布
和
的差异。
因此,
也就是我们需要的使得差异最小的 G .
详细解释 V(G,D) :
对于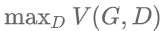 :
:
固定G ,最优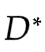 最大化:
最大化:

假设D(x) 可以表达任何函数
此时再固定 x ,则对于 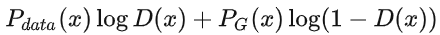 ,我们可将其看成是关于D的函数:
,我们可将其看成是关于D的函数: 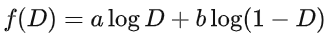

解得

即:

则此时对于原式 V(G,D) (将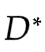 代入):
代入):
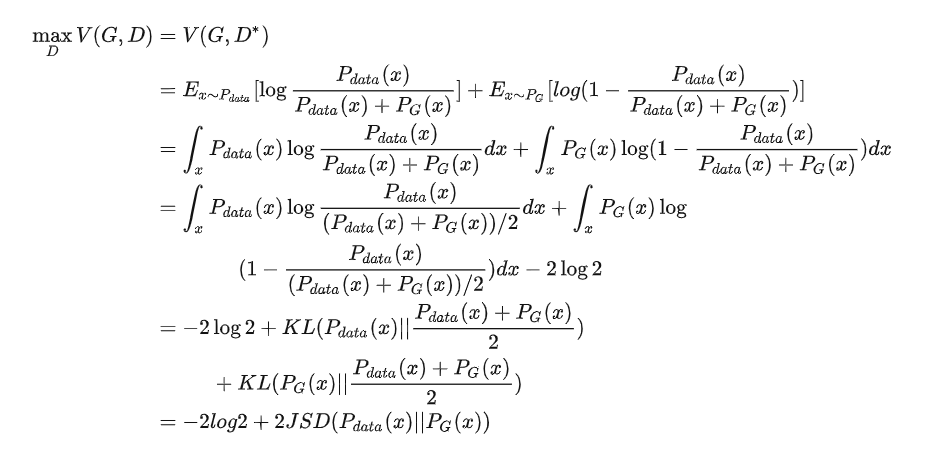
JSD表示JS散度,它是KL散度的一种变形,也表示两个分布之间的差异:
与KL散度不同,JS散度是对称的。
以上的公式推导,证明了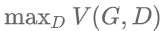 确实是衡量了
确实是衡量了 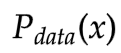 和
和 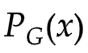 之间的差异。
之间的差异。
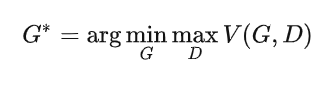
此时,最优的G:
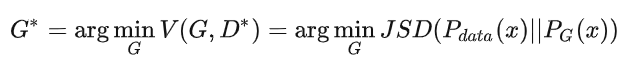
也就是使得 最小的G
最小的G
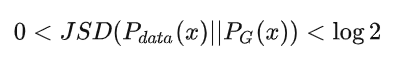
当 时,表示两个分布完全相同。
时,表示两个分布完全相同。
对于 ,令
,令 
我们该如何优化从而获得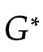 呢???
呢???
我们希望通过最小化损失函数L(G) ,找到最优的G。
这一步可以通过梯度下降实现:

具体算法参考:
第一代:
- 给定
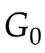 (随机初始化)
(随机初始化)
-
确定
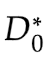 使得 V(
使得 V(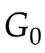 ,D) 最大。此时 V(
,D) 最大。此时 V(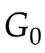 ,
,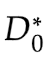 ) 表示
) 表示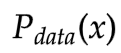 和
和 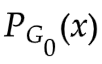 的JS散度
的JS散度 -
梯度下降:
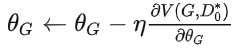 .得到
.得到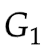
第二代:
- 给定
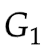
-
确定
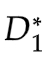 使得V(
使得V(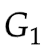 ,D) 最大。此时V(
,D) 最大。此时V(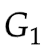 ,
,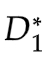 )表示
)表示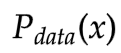 和
和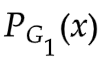 的JS散度
的JS散度 -
梯度下降:
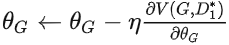 .得到
.得到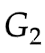
。。。
后面的依此类推
以上算法有一个问题: 如何确定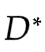 使得 V (D ,G**)**** 最大???**
使得 V (D ,G**)**** 最大???**
也就是:给定 G,如何计算 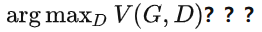
回答:
从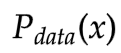 采样
采样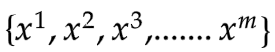
从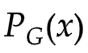 采样
采样
因此我们可以将 从期望值计算改写为对样本计算(近似估计):
从期望值计算改写为对样本计算(近似估计):

这很自然地让我们想到二分类问题中常使用的交叉熵loss
因此,我们不妨联想:
D是一个二分类器,参数是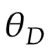
来自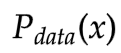 的采样
的采样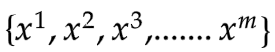 作为正样本
作为正样本
来自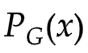 的采样
的采样 作为负样本
作为负样本
那么此时,我们就将问题转化成了一个二分类问题:
交叉熵loss大 -->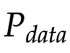 和
和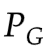 JS散度小
JS散度小
交叉熵loss小 -->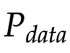 和
和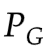 JS散度大
JS散度大
此时,D就是可以使用一个神经网络作为二分类器,那么确定D,也就是可以使用梯度下降来优化获得D的最终参数。
GAN的最终算法流程:
初始化参数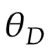 (for D)和
(for D)和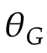 (for G)
(for G)
对于训练的每一轮:
第一部分 学习优化判别器D:
-
从
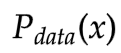 采样
采样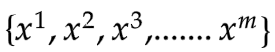
-
从
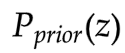 采样
采样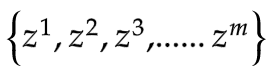
-
通过生成器
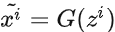 获得生成样本
获得生成样本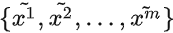
-
梯度下降更新
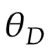 来最大化 :
来最大化 :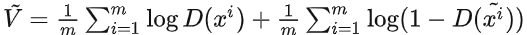 :
: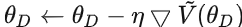
注:以上第一部分可以重复多次:此过程本质上是在测量两分布之间的JS散度
第二部分 学习优化生成器G:
- 再从
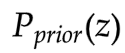 采样另一组
采样另一组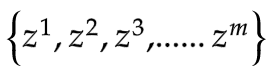
- 梯度下降更新
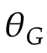 来最小化 :
来最小化 : 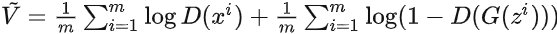 :
: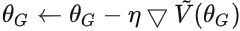 .实际上
.实际上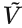 第一项与G无关,梯度下降只需最小化
第一项与G无关,梯度下降只需最小化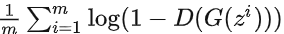 即可。
即可。
注:以上过程仅一次
最后的话:
其实在GAN之前,就已经有Auto-Encoder,VAE这样的方法来使用神经网络做生成式任务了。
GAN的最大的创新就是在于非常精妙地引入了判别器,从样本的维度解决了衡量两个分布差异的问题。
这种生成器和判别器对抗学习的模式,也必将在各种生成式任务中发挥其巨大的威力。
-
GaN
+关注
关注
19文章
1974浏览量
74460 -
生成器
+关注
关注
7文章
320浏览量
21181 -
深度学习
+关注
关注
73文章
5521浏览量
121660
发布评论请先 登录
相关推荐
你知道XGBoost背后的数学原理是什么吗?
基于GaN的开关器件
如何精确高效的完成GaN PA中的I-V曲线设计?
如何使用LL库给MCU频率F每T秒使用定时器更新事件生成一个中断?
计算机代数系统数学原理
图解:卷积神经网络数学原理解析
探讨GAN背后的数学原理(上)
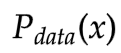
背后的数学原理在应用中得到验证
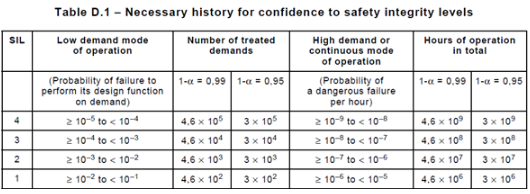




 探讨GAN背后的数学原理(下)
探讨GAN背后的数学原理(下)
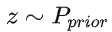 ,输出(上面已经介绍了)
,输出(上面已经介绍了)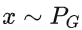
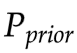 ,
,  也就是我们需要的使得差异最小的 G .
也就是我们需要的使得差异最小的 G .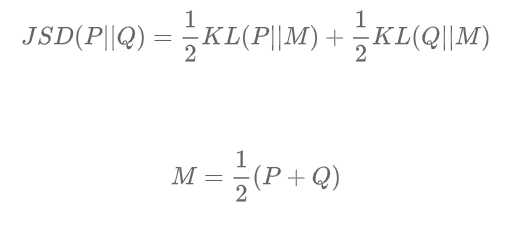
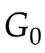 (随机初始化)
(随机初始化)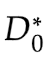 使得 V(
使得 V(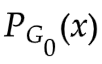 的JS散度
的JS散度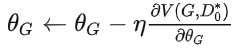 .得到
.得到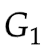
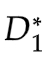 使得V(
使得V(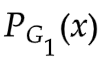 的JS散度
的JS散度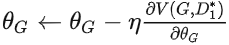 .得到
.得到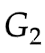
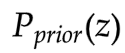 采样
采样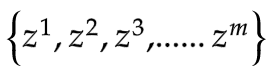
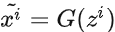 获得生成样本
获得生成样本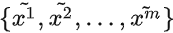
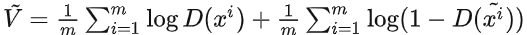 :
: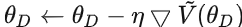
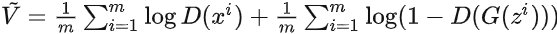 :
: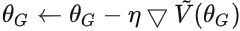 .实际上
.实际上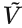 第一项与G无关,梯度下降只需最小化
第一项与G无关,梯度下降只需最小化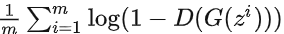 即可。
即可。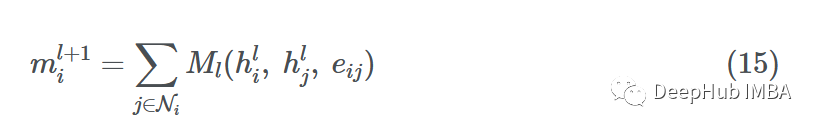










评论