PWM开关建模CCM模式
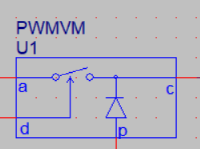
主动节点a,被动节点p,公共节点c。
端电流不变:接入电感的公共节点电流连续为Ic,而Ia=dIc,Ip=d’Ic。
端电压关系:ap两端电压始终为直流,而cp两端电压为ap的取样:Vcp=dVap。
建模结果可以用直流变压器仿真,如下
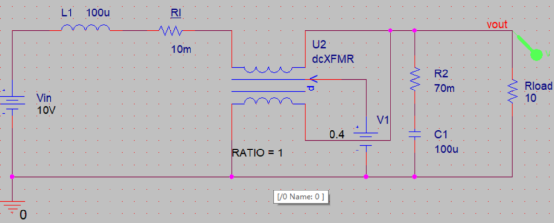
变压器控制端朝下时,左边为a,右边为c,p端是下方两个端口相连。 上图为Boost变换器大信号仿真,直流增益受电感串联的电阻影响的图形为
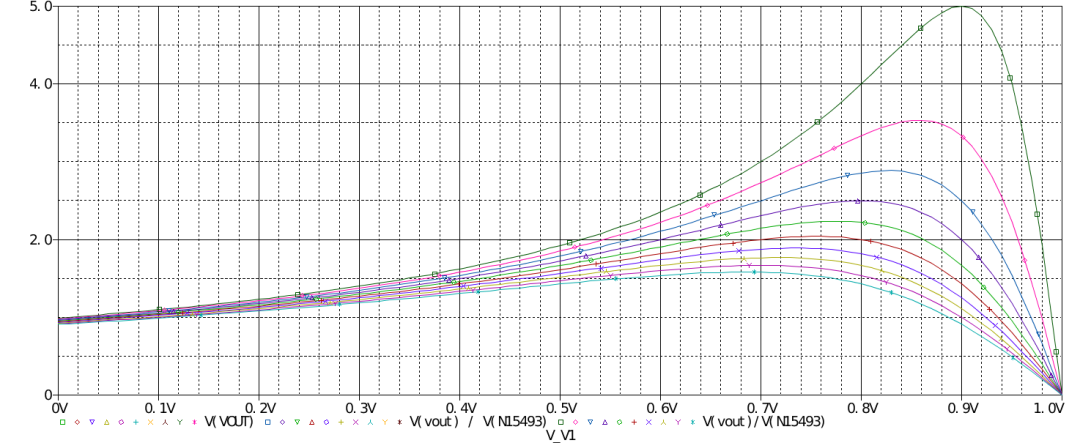
从上到下依次为100mΩ至1Ω,电感电阻对Boost的增益限制还是很大的。
也可以作小信号仿真,如下
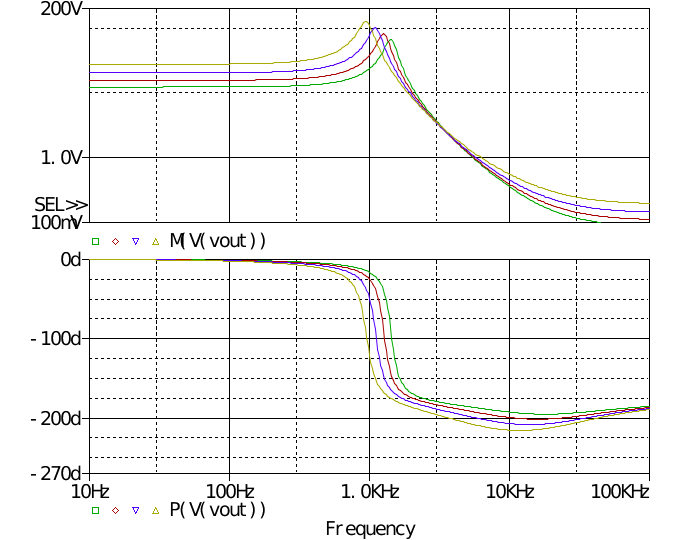
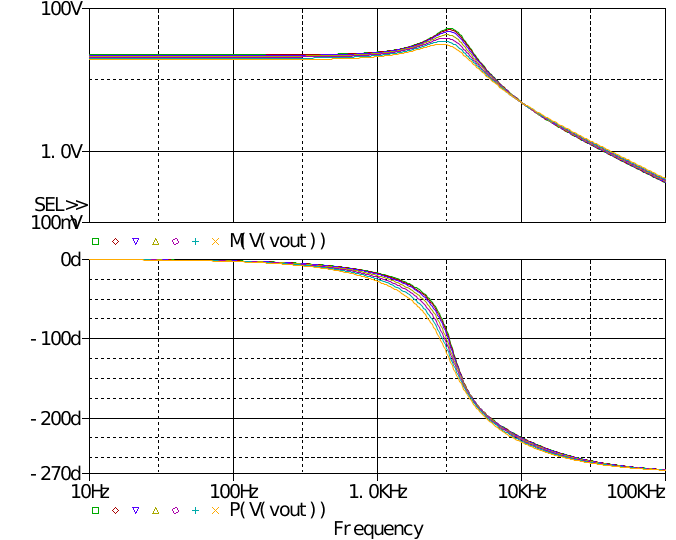
从上到下依次为D的直流量为0.4 0.3 0.2 0.1。 图中可看出RHPZ的影响,相位裕度为负几十度。 最后相位上扬的原因是ESR零点。
当然直接应用于带参数扫描的小信号分析,不利于直流工作点的稳定,于是改进模型,使输出电压稳态值稳定于常值,即引入直流反馈,其截止频率极低。 得到电感电阻变化时的响应曲线
PWM开关建模DCM模式
回到三端开关,DCM模式下端电流关系有一定变化:
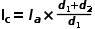
,端电压关系也变为:
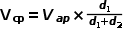
,则变压器的匝比由d变为
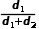
。
d~2通过峰值电流和伏秒积的关系得到,通过关系式的封装和与CCM之间切换机制的确定,构建了一个适用于两种情况下的仿真模型。
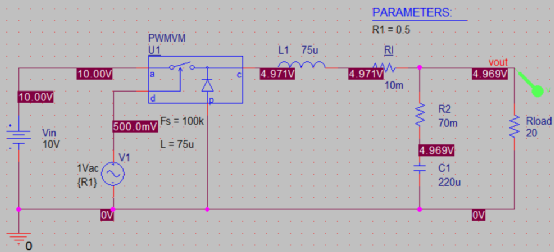
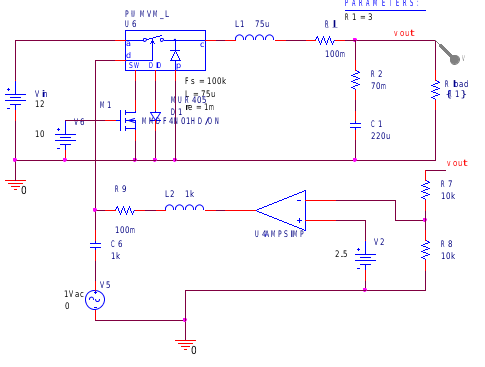
注意,该模型专为Buck使用,需要手动输入开关频率和外部电感值,以计算何时是临界导通模式,才能在CCM和DCM模式之间切换。
在D=0.5下进行交流扫描,如图电感为75uH和开关频率为100k,算出临界电流为0.166A。 分别把Rload设置为50Ω和5Ω,得到动态响应曲线
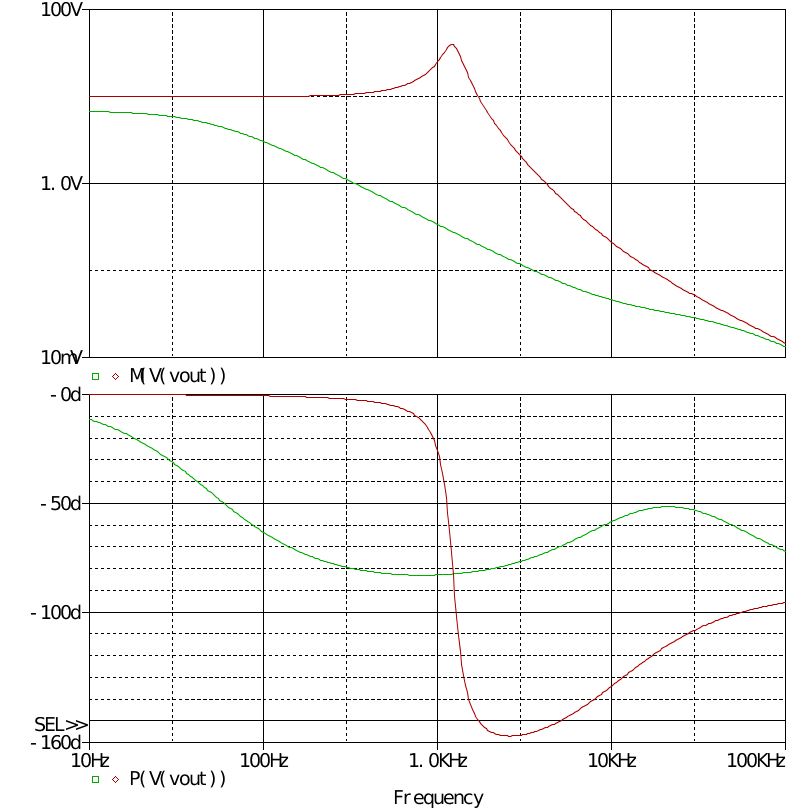
很明显,进入DCM后由二阶系统变为一阶。 电路不带有电压反馈,输出电压随负载的变化较大,因此可以同样引入直流反馈
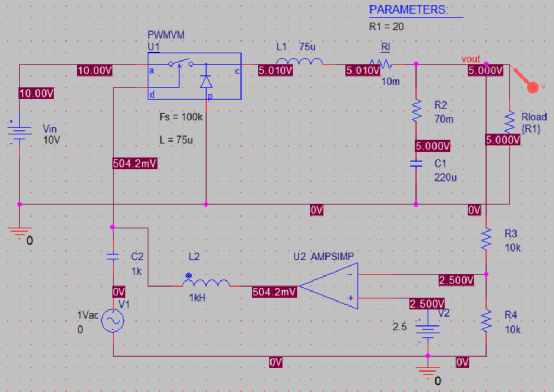
同样作CCM和DCM下的交流分析
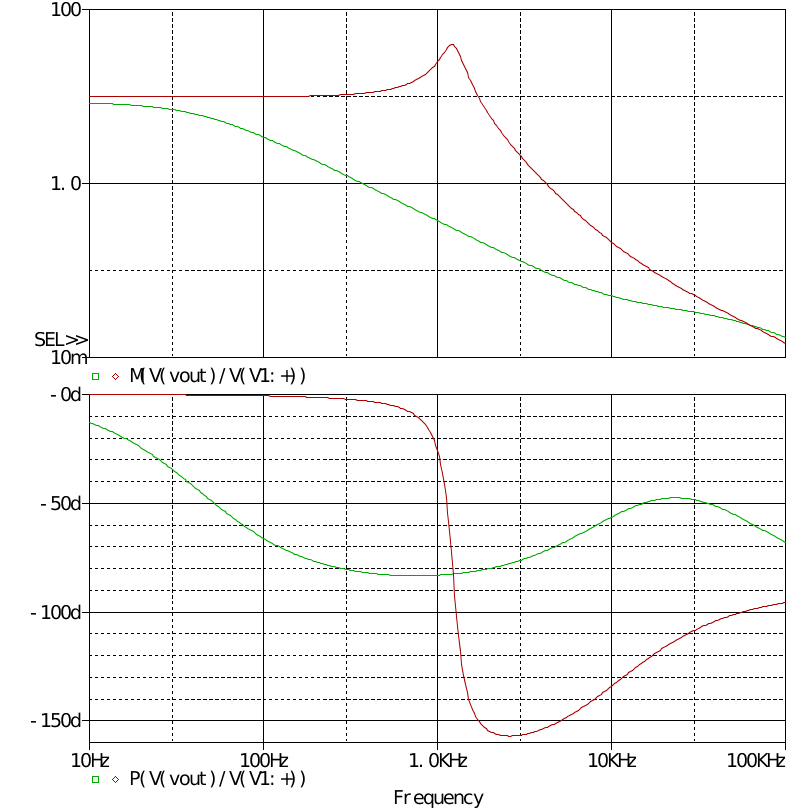
PWM调制器
已经知道,小信号模型中PWM调制器产生的增益为锯齿波幅值的倒数。
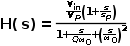
可见输入电压的变化会引起模型变化,影响动态响应。 若能消除输入电压的影响,可以令
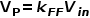
通过引入前馈增益就可以消除输入电压的影响。 压控锯齿波发生器的设计这里不赘述。 仿真时也只需在控制电压后插入一个增益为V~P的ABM源就可以。
系统时域响应测试
搭建一个三型补偿器,同样在CCM和DCM模式下分别进行测试,当参考电压从2V阶跃至2.5V时,输出电压由4V变为5V的过程
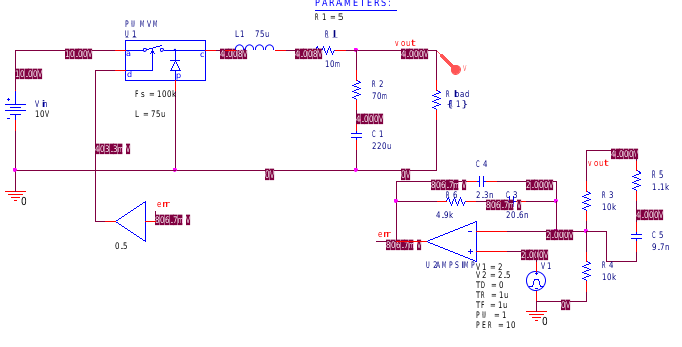
由于补偿器基于CCM模式设计,因此也无法说明太多问题。 可以看到超调量还是略大的。 对补偿器进行交流扫描
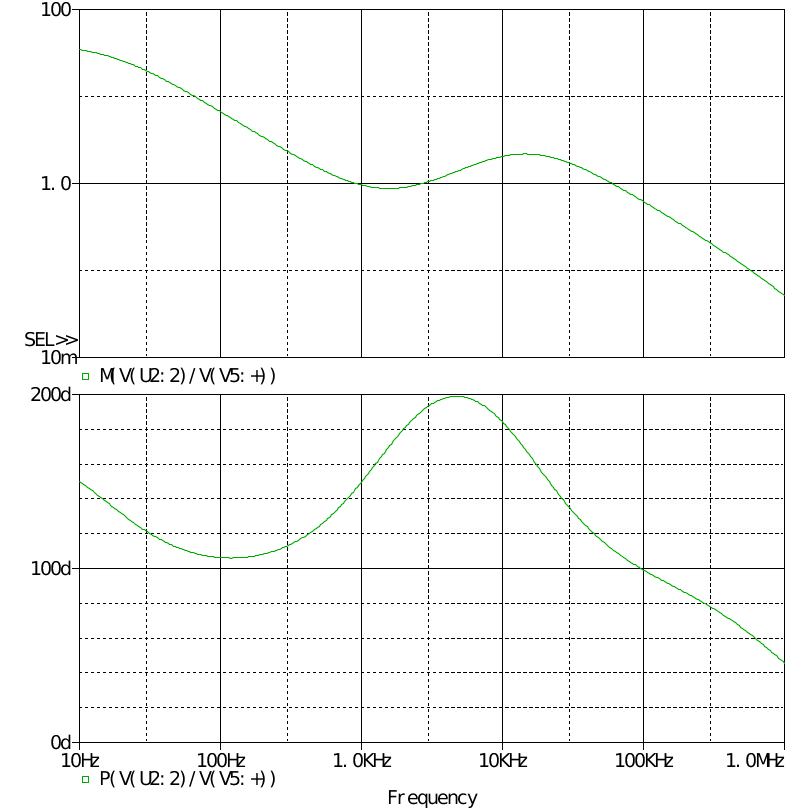
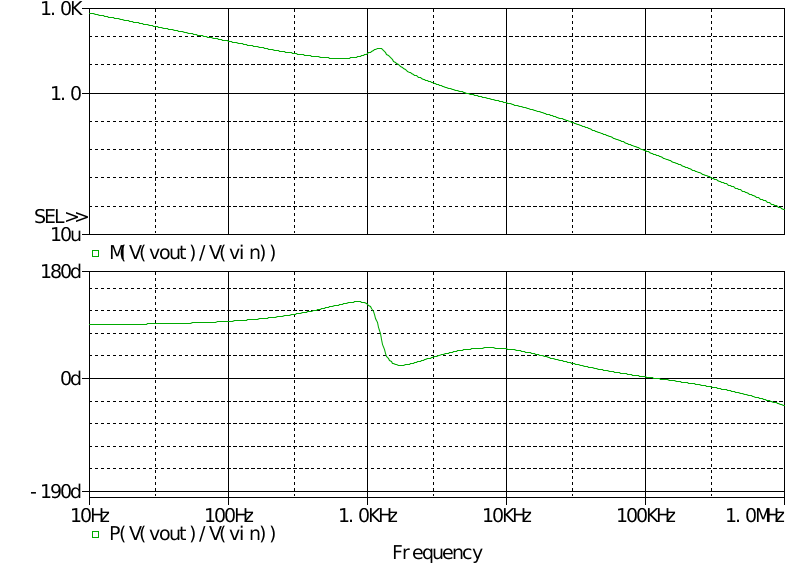
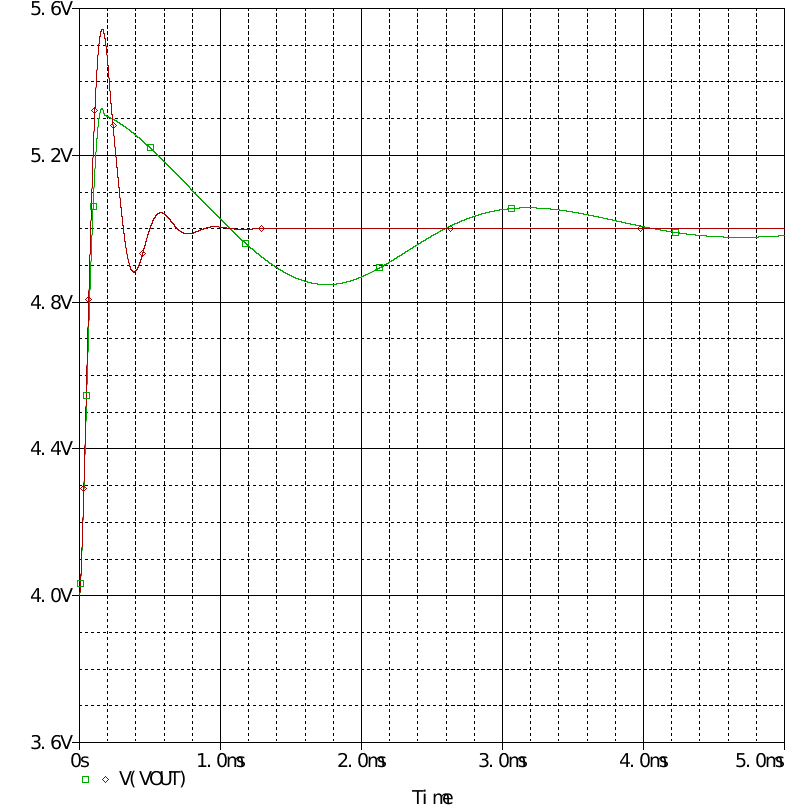
可见CCM下设计的补偿器不适用于DCM模式,在设计时造成一些麻烦。
电流模式控制
CCM下的电流模式控制占空比大于0.5时需引入斜坡补偿。 在推导电流模式控制的仿真模型时,因为控制效果与电压控制模式并无本质区别,因此PWM开关也可以沿用,即电流电压关系为
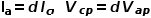
由斜坡补偿的电感电流波形,求出c端的平均电流
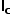
。
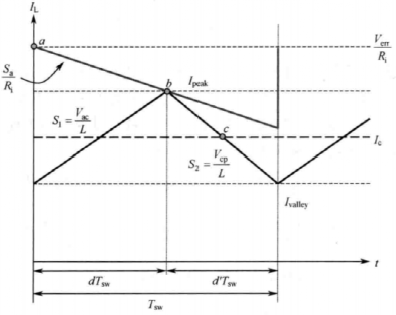
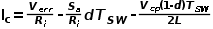
若对该表达式引入时变并求以端口电压为变量的偏导数,得到一个小信号模型,复杂就略去了。 经过推导,发现模型中存在一个等效的谐振电容,会与电感一起产生谐振以至于产生振荡,这或许就是次谐波振荡的来源。 计算品质因数与补偿斜率的关系后,推导出令品质因数为1以下时的补偿斜率
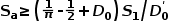
D~0表示稳态占空比。 这是选择补偿斜率的方法之一。 或者简单地选择为截止时斜率的一半,前提是电路不进入BCM模式。
DCM时仍需要斜坡补偿(原因没说),因为多了一个0电流模态,可得c端电流平均值
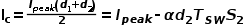
而对有斜坡补偿的电流峰值为
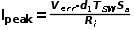
可以得到
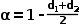
和电流平均值的表达式
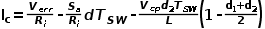
当d2=1-d1时就变成CCM模式。 通过以上式子可以得到d2等参数,从而构建一个CCM和DCM通用的仿真模型,形式上与电压模式控制并无差异。
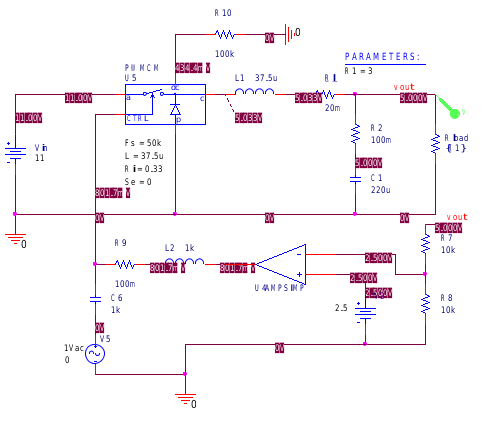
注意的是,库中的PWMCM包含谐振电容,而PWMCMX为了避免瞬态仿真中的收敛问题,去掉了谐振电容,瞬态仿真时可以用这个模型。
与之前一致作直流闭环下的小信号仿真,先设置S ~a=0,即没有斜坡补偿的电流模式控制,得到波特图
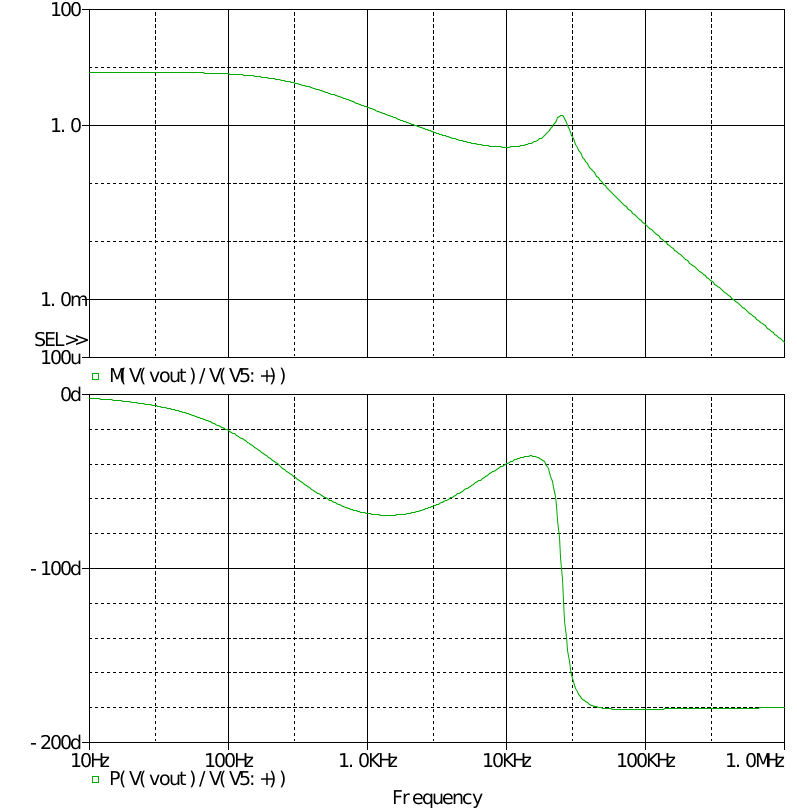
可见未补偿时在高频处存在一个谐振峰,在此例中这个谐振峰穿越了0dB线,将会影响性能,与理论预测的一致。
再进行斜坡补偿,如前所述选择补偿斜率,这里电路运行于CCM模式,假定不会进入BCM,可以直接取为截止斜率(也可以是导通斜率)的一半为
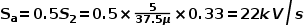
其中0.33是电流取样电阻的阻值。 若取导通斜率的一半则为26.4kV/s。 补偿后的波特图为
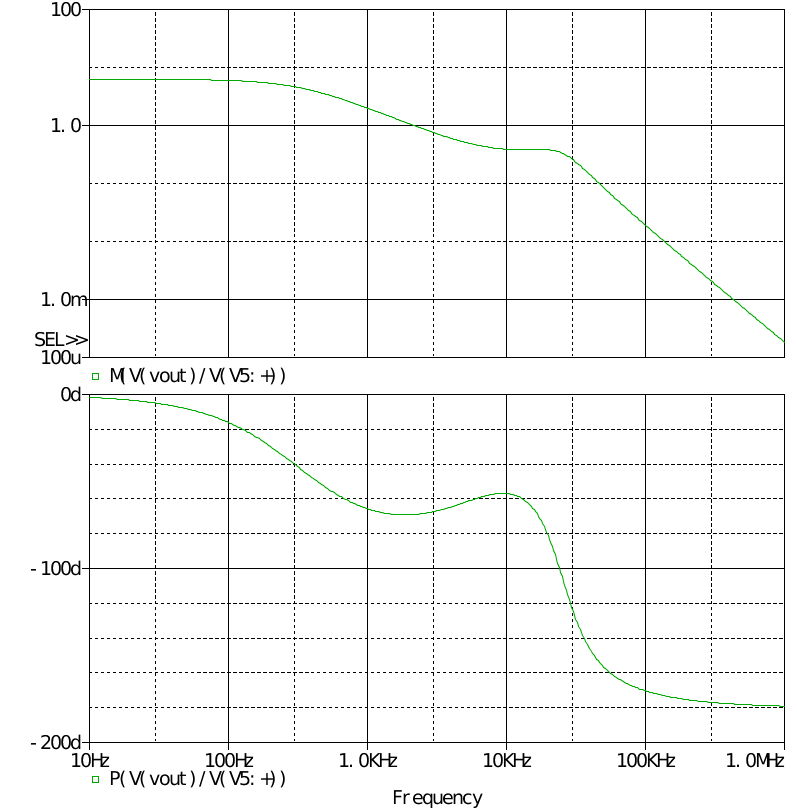
则消除了谐振峰,稳定性改善了许多。
占空比信号直接生成
一般将电压模式控制称为直接占空比控制,将电流模式控制称为间接占空比控制,因为电流模式控制中多了一个误差电压转化为峰值电流的环节。 通过直接推导占空比的表达式然后构建模型,理论上可以实现,但CCM下的模型似乎并不能预测到高频的谐振点。 DCM下的模型运行良好。
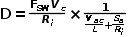
考虑寄生参数
纹波电流在输入电容和输出电容存在的ESR上形成纹波电压,导致PWM开关模型的
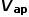
和
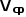
并非恒定值,而是叠加了一个纹波。 如果把寄生参数考虑进PWM开关中,可以直接构建一个
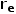
,随拓扑的变化而变化。 由端电压关系有
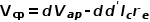
即在p端加入一个阻值为
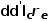
的电阻。
再考虑MOS管导通电阻和二极管导通压降的影响。 流经MOS和二极管的电流不变,而且在PWM开关中已经定义好了分别是a端和p端,那么最终变化的也是电压波形。
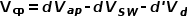
后两项可以用两个电压源实现,但开关SW和二极管的具体压降由流经的电流和选择的器件参数决定,这时就需要外接实际的管子,然后PWM开关模型再通过管子上的实际压降来计算得出模型参数。
注意的是外接MOS管和二极管的实质是测量其上的导通电压,而不是让它们参与变换器的工作,因此MOS管直接用一个直流电源维持导通,二极管也直接阴极接地,维持导通。
电流模式下的模型也如上所述。
这些损耗模型因为是利用电流平均值生成损耗电压值,而实际中损耗能量是与电流有效值有关,其差别有时不可忽略,所以精确性并非最佳。
边界导通模式的PWM模型
频率变化的BCM具有特别的优点:避免反向恢复的影响; 电路模型退化成一阶; 易于实现软开关。 其控制思想就是让电感电流到0时就打开开关管。 用于反激拓扑中称为准谐振拓扑,若利用关断振铃插入延迟,则可以实现软开关。
BCM下,端电流恰为峰值的一半
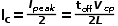
模型以导通时间

为输入参数。
四阶变换器Cuk电路例子
同样用书中给出的PWM开关模型可以构建其他拓扑,Cuk电路及其交流响应如下
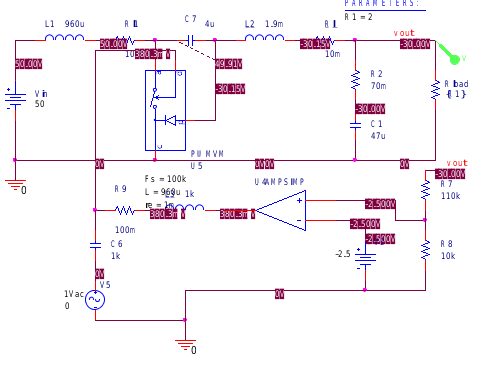
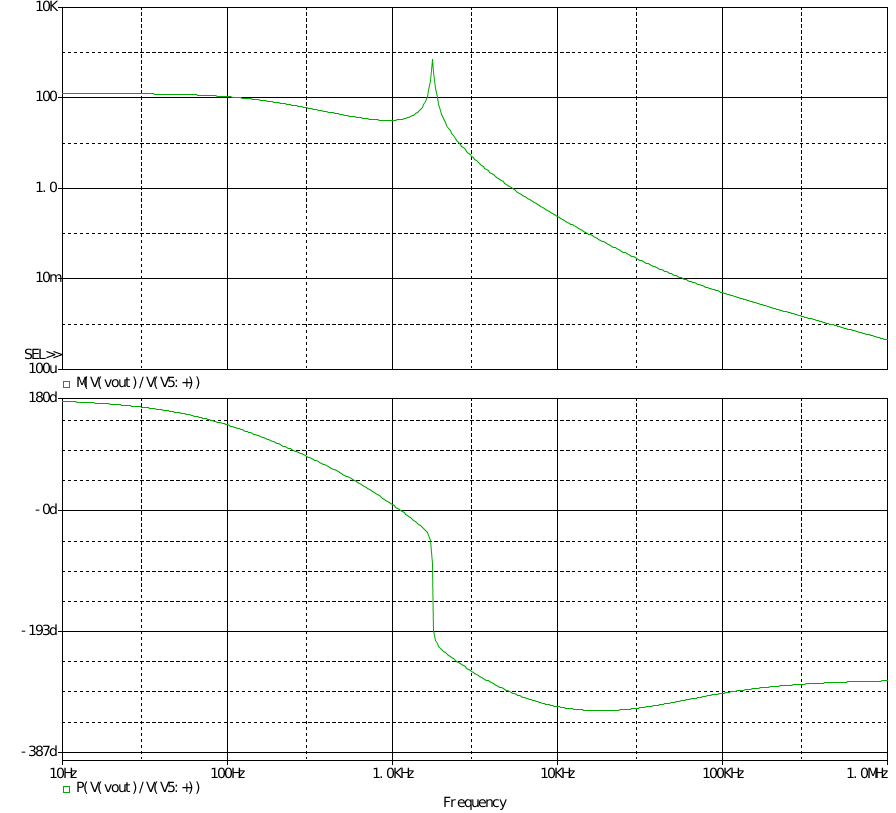
明显可以看出相移达到-320°,确是四阶系统,后面因ESR零点略有上升。 在截止频率处相移为-290°,相位裕度为-110°,极易振荡。 以下是在占空比输入阶跃信号时的输出响应。
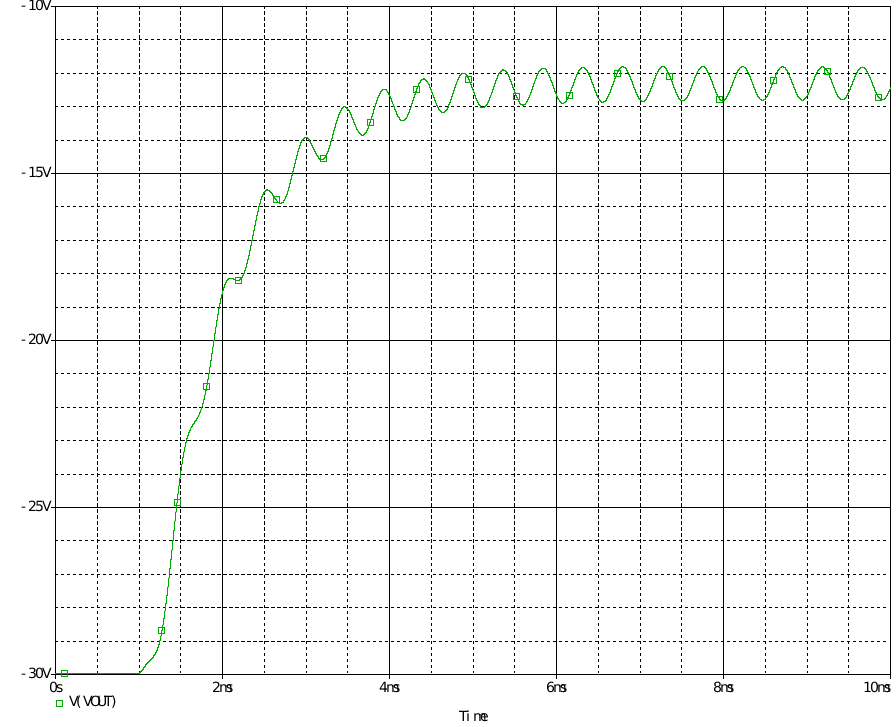
而下图是把闭环的参考电压换成阶跃电压源,得出发散振荡的结果
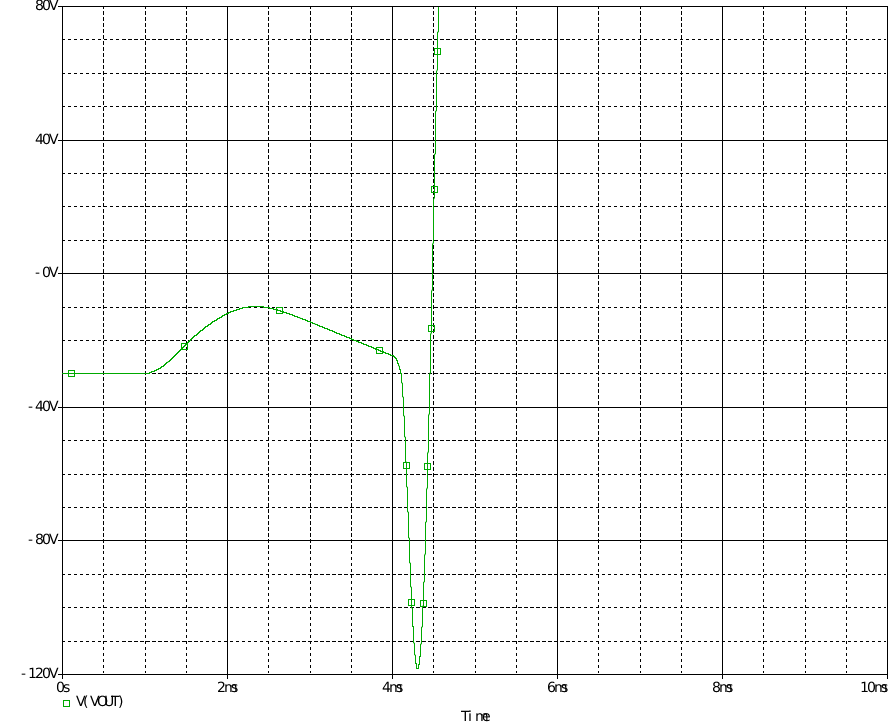
-
开关
+关注
关注
19文章
3220浏览量
94119 -
PWM
+关注
关注
114文章
5209浏览量
215690 -
电压
+关注
关注
45文章
5652浏览量
116603 -
DCM
+关注
关注
0文章
161浏览量
26659 -
CCM
+关注
关注
0文章
151浏览量
24242
发布评论请先 登录
相关推荐
开关电源Buck电路CCM及DCM工作模式

开关电源Buck电路CCM与DCM工作模式有什么区别?

开关电源Buck电路CCM和DCM工作模式





 PWM开关建模CCM和DCM模式讲解
PWM开关建模CCM和DCM模式讲解










评论