数字逻辑器件可分为通用逻辑器件和ASIC两种类型。从理论上讲,应用通用逻辑器件(如4000系列和74HC系列)、微处理器和存储器可以构建任何数字系统。但是,通用逻辑器件的规模一般都比较小,而且功能固定,在设计复杂数字系统时需要使用大量芯片,这会导致系统的体积难以缩小、功耗难以降低,同时受到器件传输延迟和芯片之间布线延迟的影响,使得系统的工作速度难以有效提高。
以2015年电子设计竞赛题-数字频率计的设计进行分析。竞赛题目的要求设计并制作一台闸门时间为1s的数字频率计,能够测量1Hz~100MHz矩形波信号的频率。要求频率测量的相对误差不大于0.01%(10^-4)。
频率是指周期信号在单位时间内的变化次数。频率计用于测量周期信号的频率,有直接法、周期法和等精度3种测频方法。
直接测频法的原理电路如图1(a)所示,其中与门的两个输入端分别接被测信号Fx和闸门信号G(Gate signal),与门的输出作为计数器的时钟。由闸门信号G控制计数器在固定的时间范围内统计被测信号的脉冲数,如图1(b)所示,脉冲数与时间之比即为被测信号的频率。取闸门信号G的作用时间为1s时,计数器的计数值即为被测信号的频率值。
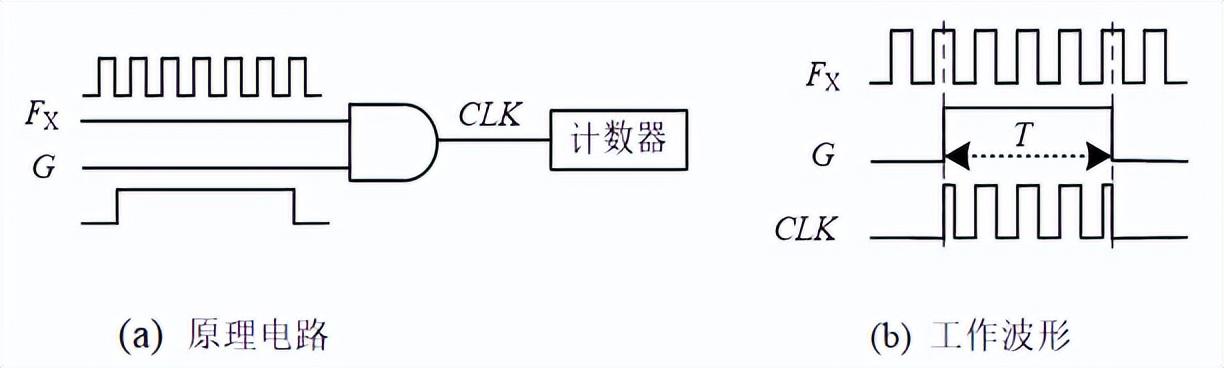
图1 直接测频法原理
直接测频法能够测量信号频率的范围与闸门信号G的作用时间和计数器的容量有关。当闸门信号的作用时间为1s时,如果需要测量频率为10kHz的信号时,那么要求计数器的容量为10^4,基于中、小规模通用逻辑器件实现时可以应用4片十进制计数器74HC160级联实现。如果需要将测频范围扩展为100MHz,在闸门信号的作用时间同样为1s的情况下,则要求计数器的容量为10^8,这就需要用8片74HC160级联实现。一般地,在闸门信号作用时间固定的情况下,测量信号频率的范围越大,则计数所用的芯片越多,因而电路就越复杂。
当计数器的容量固定时,虽然可以通过缩短闸门信号的作用时间来扩展频率测量范围,但是会降低频率测量的精度。这是因为,在直接测频法中,闸门信号G的作用时间是随机的,在计数过程中可能会存在1个脉冲的计数误差。
直接测频法中计数误差的成因分析如图2所示,其中被测信号Fx1、Fx2和Fx3的频率完全相同。设闸门信号G与被测信号Fx1同步,计数器在时钟脉冲的上升沿工作。
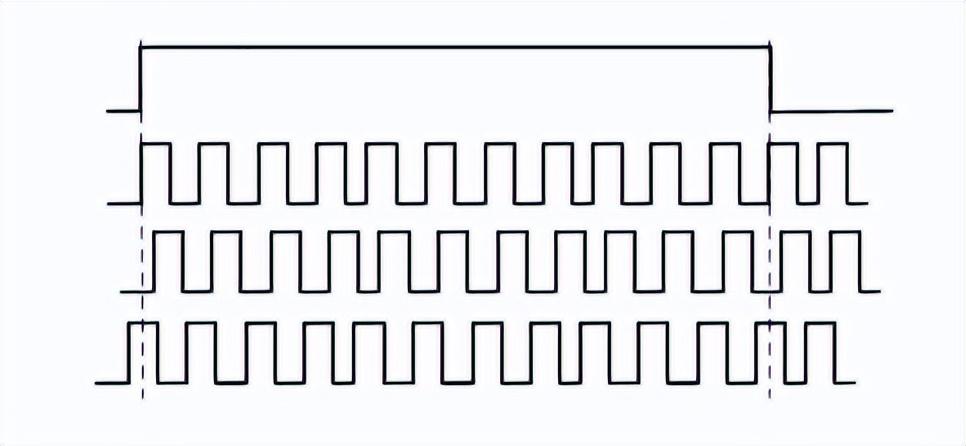
图2 直接测频法误差成因分析
在闸门信号G的作用下,如果对信号Fx1的计数值为N,则对信号Fx2的计数值为N-1,对信号Fx3的计数值为N+1。所以,取闸门信号的作用时间为1s时,直接测频率法的计数误差为±1Hz;取闸门信号的作用时间为0.1s时,则计数误差为±10Hz。
另外,基于中、小规模通用逻辑器件设计时还存在一个问题:频率计的测频范围受计数器芯片性能的限制。查阅NI公司的器件资料可知,74HC160从时钟到输出(clock to Q)的传输延迟时间为18ns,典型工作频率为40MHz,如图3所示,极限工作频率为43MHz。同时,应用多片74HC160级联扩展计数容量时,还需要考虑芯片与芯片之间布线传输延迟的影响。因此,虽然用8片74HC160级联理论上能够扩展出108进制计数器,但实际上却无法测量40MHz以上信号的频率。

图3 74HC160 器件资料片段
直接测频法的原理简单,但是由于理论上存在一个脉冲的计数误差,所以被测信号的频率越低,直接测频法的相对误差越大,存在着测量实时性和测量精度之间的矛盾。例如,取闸门信号的作用时间为1s,当被测信号的频率为1000Hz时,理论上频率测量的相对误差为0.1%,而当被测信号的频率为10Hz时,则频率测量的相对误差高达10%。
应用直接测频法虽然可以通过增加闸门信号的作用时间来减小测频误差,但是,对于频率为10Hz的信号,若要求频率测量的相对误差不大于0.01%,则闸门信号的作用时间最短为1000s。显然,这么长的测量时间是无法接受的,所以直接测频法不适合测量低频信号的频率。
从图2可以看出,如果能够控制闸门信号G与被测信号FX同步,那么就能够消除计数误差,因而从理论上讲,频率测量的相对误差为0。
等精度测频法就是通过控制闸门信号与被测信号同步从而消除了计数误差,其原理电路如图4所示,将闸门信号G作为边沿D触发器的输入,被测信号Fx作为D触发器的时钟脉冲时,D触发器输出的新闸门信号SG(Synchronous Gate signal)与Fx同步。
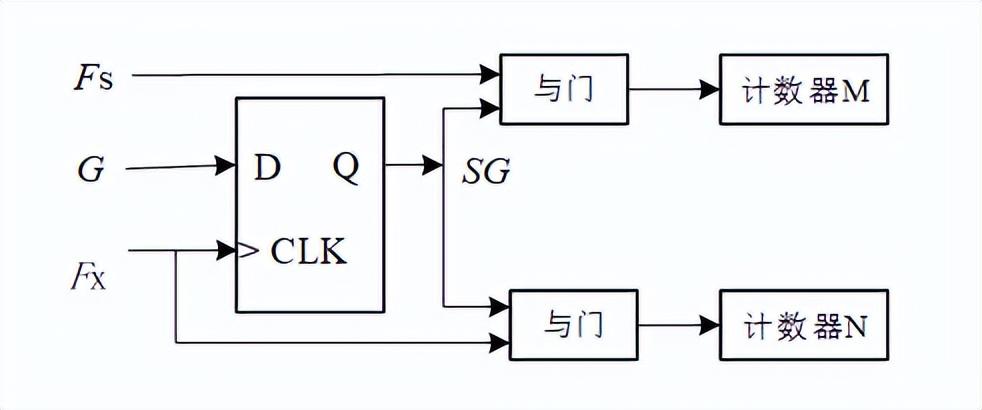
图4 等精度测频法原理电路
等精度测频法的工作原理是:当闸门信号G跳变为高电平时,只有当被测信号FX的上升沿到来时D触发器输出的新闸门信号SG才能跳变为高电平;当闸门信号G跳变为低电平时,同样只有当被测信号Fx的上升沿到来时D触发器输出的新闸门信号SG才能跳变为低电平。因此,D触发器输出的新闸门信号SG与被测信号Fx严格同步,所以用新闸门信号控制计数器时,就能够消除计数误差。但是,由于新闸门信号SG的作用时间受被测信号Fx的控制,虽然取原闸门信号G的作用时间为1s,但新闸门信号的作用时间不一定为1s,因而计数器N中的计数值并不能代表被测信号的频率值。改进的方法是,再添加一个与门和计数器M,在新闸门信号SG的作用时间内同时对被测信号Fx和一个标准频率信号Fs进行计数,应用两个计数器的计数时间完全相同的关系推算出被测信号的频率值。
等精度测频法被测信号频率的计算原理如图5所示。若将新闸门信号SG的作用时间记为TD,标准频率信号Fs的周期记为Ts,被测信号Fx的周期记为Tx,在TD时间内对标准频率信号和被测信号的计数值分别记为Ns和Nx,则闸门信号SG的作用时间TD可以精确地表示为
TD=Nx×Tx
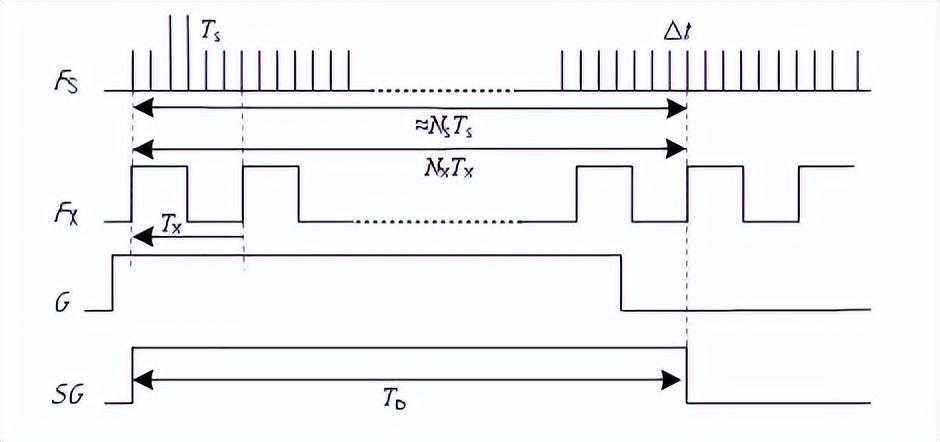
图5 等精度测频法工作波形
虽然D触发器输出的新闸门信号SG与被测信号Fx严格同步,但并不一定与标准频率信号Fs同步,所以从理论上讲,在TD时间内对标准信号进行计数,仍然可能存在一个脉冲的计数误差。因此,若用Ns×Ts表示TD时,则
TD≈Ns×Ts
如果取标准信号的频率很高,使得Ts<
Ns×Ts≈Nx×Tx
若将标准频率信号和被测信号的频率分别用fs和fx表示,并将Ts=1/fs和Tx=1/fx代入上式整理可得
fx≈(Nx/Ns)×fs
其中,Ns和Nx分别为两个计数器的计数值。根据上式即可计算出被测信号的频率值。下面对等精度测频的相对误差进行分析。
设用Ns×Ts表示TD的误差记为△t,则
△t=TD-Ns×Ts
设被测信号频率的精确值记为fx0。由于TD=Nx×Tx0,所以fx0=Nx/TD,因此频率测量的相对误差δ可以表示为
δ =(fx-fx0)/fx0=fx/fx0-1
≈(fs×Nx/Ns) /(Nx/TD) -1
=TD/(Ts×Ns)-1
=(TD-Ts×Ns)/(Ts×Ns)
=△t/(Ts×Ns)
=△t/(TD-△t)
由于△t最大为一个标准频率信号的周期,所以标准频率信号的周期Ts<
δ≈Ts/TD
由上式可以看出,等精度测频法频率测量的相对误差与被测信号的频率无关,只取决于标准信号周期Ts与新闸门信号SG作用时间TD的比值。因此,取标准信号的频率越高,或者闸门信号的作用时间越长,则频率测量的相对误差就越小。
采用100MHz标准信号时,闸门信号的作用时间TD与测频的相对误差δ之间的关系如表1所示。可以看出,当闸门信号SG的作用时间为1s时,频率测量的相对误差约为0.000001%(10^-8),完全满足竞赛题目的精度要求。
表1 闸门信号作用时间与频率测量误差关系表
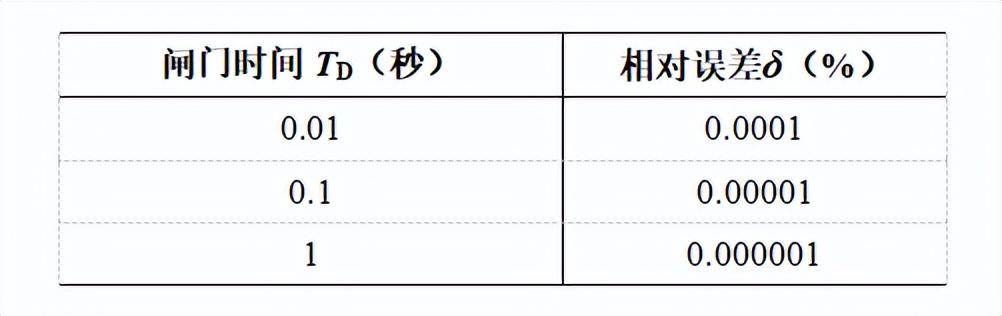
等精度测频法频率测量的精度很高,但是需要应用乘法和除法运算来计算被测信号的频率值。取闸门信号G的作用时间为1s、标准信号的频率为100MHz时,如果要求能够测量100MHz信号的频率时,不但需要应用27位二进制计数器(因为226<108<227)分别对被测信号Fx和标准频率信号Fs进行计数,还需要应用27位二进制乘法器和54位二进制除法器来计算被测信号的频率值。若应用74系列中、小规模通用逻辑器件来搭建27位乘法器和54位除法器,其电路的复杂程度是难以想象的。
那么,如何实现等精度频率测量呢?提供以下3种方案:
(1)基于微控制器和PLD实现。
应用MCS-51、MSP430或者STM32等系列微控制器虽然计算乘除法很方便,但是对高频信号进行计数则相对困难。若应用微控制器内部的计数/定时器来统计被测信号和标准信号的计数值,则会受到内部计数/定时器性能的限制,很难有效测量MHz级及以上信号的频率。
如果在微控制器外围扩展中规模集成计数器(如74HC161)进行计数,然后通过I/O口读取被测信号和标准信号的计数值,通过编程计算被测信号的频率值,不但外围电路复杂,而且同样会受集成计数器芯片性能的限制,测频范围难以有效扩展。因此,推荐应用可编程逻辑器件CPLD或者FPGA进行计数,基于微处理器计算乘除法。
(2)应用EDA技术,基于IP核实现。
应用EDA技术实现等精度频率计时,可以直接用硬件描述语言描述所需要的计数器,然后在可编程逻辑器件中实现,不但不会受到具体器件功能的限制,而且计数器能够正常工作的最高频率远远超过100MHz。另外,还可以定制EDA软件中的乘法IP和除法IP来实现乘除法运算,只需要将计算得到的二进制频率值转换为BCD码显示即可。
(3)应用EDA技术,基于片上系统实现。
在FPGA中搭建软核处理器系统或者直接应用片内硬核处理器,用硬件描述语言描述所需要的计数器,应用片上处理器控制测频过程,计算乘除法以及频率转换值与显示。
综上分析,要解决电子竞赛中数字频率计的设计问题,无论采用以上哪种方案设计等精度频率计,都必须应用EDA技术。
另外,等精度频率计虽然测频范围宽,而且精度高,但测试表明,在闸门作用时间为1s的情况下,还不能满足1Hz信号频率测量的精度要求。为此,还需要设计周期法频率计,与直接法频率计或者等精度频率计相配合,才能实现满足竞赛精度要求的1Hz~100MHz频率计,而设计周期法频率计需要应用图6所示的状态机来统计被测信号两个相邻脉冲之间的脉冲数,然后通过脉冲数计算出被测信号的周期,再根据频率与周期之间的倒数关系应用除法计算出频率值,同样需要学习EDA技术。
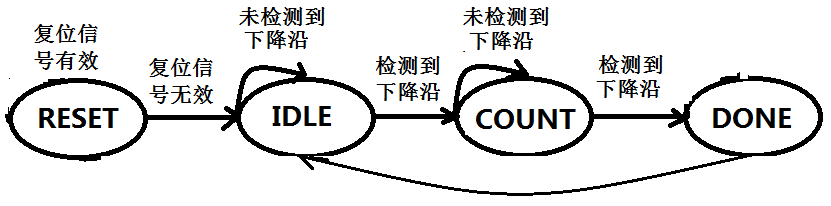
图6 周期测量状态机
-
FPGA
+关注
关注
1631文章
21808浏览量
606804 -
asic
+关注
关注
34文章
1206浏览量
120891 -
微处理器
+关注
关注
11文章
2275浏览量
82866 -
逻辑器件
+关注
关注
0文章
88浏览量
20167 -
数字频率计
+关注
关注
17文章
104浏览量
35837
发布评论请先 登录
相关推荐
数字频率计
设计简易数字频率计





 数字频率计的三种测频方法
数字频率计的三种测频方法










评论