以21700锂离子电池组为研究对象,对不同排布方式下的锂电池分别控制电池间距、对流换热系数和相变材料(PCM)导热率,并对其进行有限元仿真。研究了电池间距、对流换热系数和PCM导热率对相变电池热管理系统(BTMS)下不同排布方式(长方形、四边形、六边形)的电池组温度场的影响。结果表明:当电池间距为4mm和6mm时,3者具有近似的最高温度,而当电池间距为2mm和1mm时,长方形排布的电池组最高温度最大,在2mm时长方形排布的电池组最大温升分别为四边形排布下和六边形排布下的电池组的105.86%和108.25%,而3者的温差均随间距增大,总体呈现出变小的趋势;在不同的对流换热系数下,长方形排布的电池组最高温度总是最大而四边形最小,随着对流换热系数的增大,3者温差呈现出变大的趋势;随着PCM导热系数的增大,3者的最高温度均不断下降且下降速率越来越小,在5种不同PCM导热系数下,长方形排布的电池组最大温升平均是四边形排布和六边形排布电池组的105.31%和106.02%,3者的潜热储热阶段的温差均有减小,显热阶段对长方形和六边形的温差没有影响,四边形的温差却不断增大。综合考虑最高温度和温差,采用六边形排布的锂电池组在PCM热管理下的热性能最佳。
作者:郭茶秀 魏金宇
郑州大学 机械与动力工程学院,河南郑州
锂离子电池作为一种具有高能量密度且循环寿命长的电化学储能系统,已经在电动汽车市场中有了广泛的应用。然而,锂离子电池在各种条件下的热问题研究和电池热管理系统并没有得到充分的解决。因此,对于基于锂离子的电动汽车,需要一种有效的电池热管理系统(batterythermalmanagementsystem,BTMS)来快速散去电池组内部产生的热量。空气冷却作为最传统的冷却方式 ^[1-5]^ ,由于空气本身较低的导热率,很难满足电池在高功率放电时的散热需求;液冷是如今BTMS应用最广泛的冷却方式 ^[6-8]^ ,具有散热效果好、速度快等优点。但其一般都有着较为复杂的结构和较高的价格,而且对密封性要求较高,一般在极端情况下使用。Hal-laj等 ^[9]^ 首先提出了将相变材料用于BTMS的想法。Sabbah等 ^[10]^ 研究了在不同放电速率和环境温度下PCM(phasechangematerial)和空气热管理系统的性能,结果表明,在高放电倍率和高温环境下,空气冷却需要大量的功耗才能达到PCM热管理系统的效果。在研究PCM散热的过程中研究人员发现,当电池温度没有超过PCM熔点时,其对电池的最高温度和温差的升高有着很好的抑制作用。
前人对于PCM散热和电池的排布优化已经进行了相关的研究,张晓光等 ^[11]^ 对电池间距的均匀排布和不均匀排布情况进行了研究,在相同体积的相变材料中对电池间距进行非均匀排布,最优排布的最大温差比优化前降低了34%。以上对电池排布的研究,都选择了间距为变量,采用均匀间距或非均匀间距,但都没有对排布方式进行研究,因此作者选择排布方式为变量,研究了电池间距、对流换热系数和PCM导热率对相变BTMS下不同排布方式的电池组温度场的影响。
本文以21700锂离子电池组为研究对象,通过对不同排布方式下的锂电池分别控制电池间距、对流换热系数和PCM导热率,并分别进行仿真分析,研究电池间距、对流换热系数和PCM导热率的变化对不同排布方式下以相同比体积的相变材料包裹下21700锂离子电池的最高温度和温差的影响。
01数值方法
几何模型
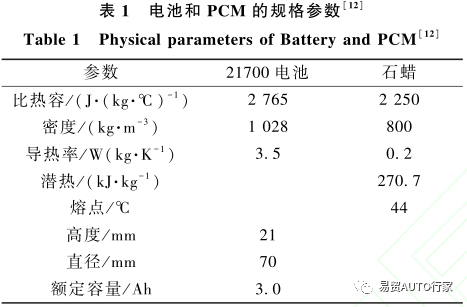
采用模拟软件 AnsysFluent19.2,以 21700 型圆柱形锂离子电池为研究对象,以数值模拟的方法模拟了使用 PCM( 石蜡) 热管理系统下的锂电池不同排布方式的传热过程。为了研究不同排布方式对 PCM 热管理系统的影响,设计了以长方形、四边形和六边形排布的 3 种电池组,以相同比体积 ( 相变材料体积与电池个数比值)的相变材料包裹电池。锂电池和相变材料物性参数如表 1 所示。
电池产热模型
在进行数值分析前,要先得到电池的产热功率,通常用Bernardi等 ^[13]^ 提出的产热公式得到与实验中的实际结果较为符合的产热功率,所以本文中使用Bernardi产热公式来计算电池的产热功率:
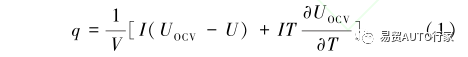
式中:q为电池的产热功率,W/m3;I为电池工作时的电流,A;V为电池的体积,m3;T为电池的初始热力学温度,K;UOCV为电池的开路电压,V;U为电池的端电压,V;∂UOCV∂T为电池的熵系数,mV/K。
Chen等 ^[12]^ 实验得到了21700型锂电池在35℃下以4C倍率放电时的开路电压、端电压和熵系数,如图1所示。结合表1的电池参数在拟合后,可以得到4C倍率放电情况下的电池产热功率-时间关系式:
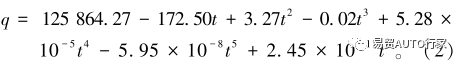
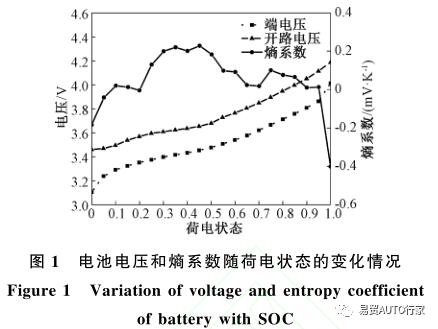
产热模型验证
为了验证产热公式的可靠性,使用Fluent19.2对单个电池在自然对流下以4C倍率放电的产热情况进行模拟并与实验情况进行对比。环境温度设置为35℃,自然对流系数为10W/(m2·K),结果如图2所示。
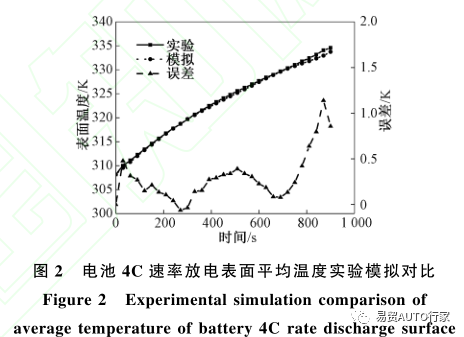
由图2中数据可以看出,实验和模拟中电池的温升都是先快后慢,总体趋势相同,且最大误差仅为1.14K,实验与模拟结果误差不超过5%,由此可以看出,产热公式具有较高的精确性和可靠性,可以满足计算模拟的需求。
网格无关性验证
为了减少网格数量对实验结果产生的影响并且节省计算时间,需要选取合适大小的网格进行计算。图3为网格无关性验证。
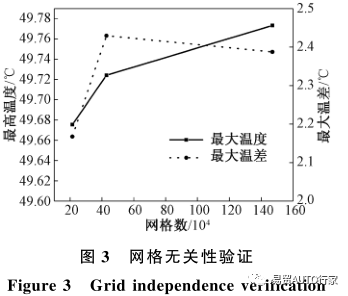
从图3可以看出,当网格数从214344增加到428016时,最高温度和最大温差都变化较大,而继续增大网格数则变化不大。所以,为了有效利用计算资源并保证模拟的精确性,本文的模拟采用网格数为428016的网格模型进行计算。
控制方程
为了简化计算过程,首先要对传热过程做出以下假设。
①电池内部物性参数和产热是均匀的;②PCM热物性参数各向同性,且不随温度变化;③PCM内部只考虑热传导,忽略液态PCM的热对流;④不考虑传热过程中的辐射。
模拟时电池和PCM的初始温度和环境温度都为35℃,空气自然对流系数为10W/(m2·K)。电池内部传热方程:
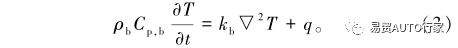
相变材料内部传热方程:
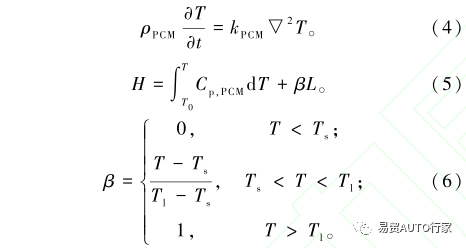
电池与 PCM 接触面的边界条件:
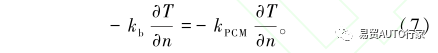
外表面边界条件:
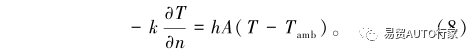
式中:ρb为电池的密度,kg/m3;Cp,b为电池的比热容,J/(kg·K);kb为电池的导热率,W/(m·K);∂T∂t为温度梯度;q为体热源,W;ρPCM为PCM的密度kg/m3;Cp,PCM为电池的比热容,J/(kg·K);kPCM为电池的导热率W/(m·K);β为PCM的液相分数;L为PCM的潜热,kJ/kg;Ts和Tl分别为相变开始和终止的温度,K;h为自然对流系数,取10W/(m2·K);Tamb为环境温度,取35℃。
02结果与讨论
排布方式对电池温度场分布的影响
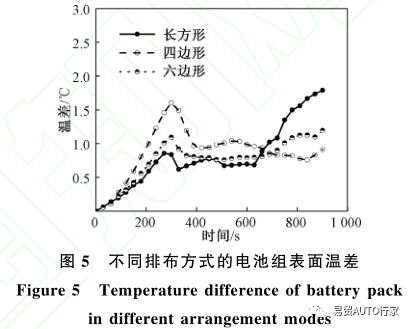
图4和图5显示了电池在4C速率放电情况下,不同排布方式的电池组表面最高温度和温差随时间的变化情况。
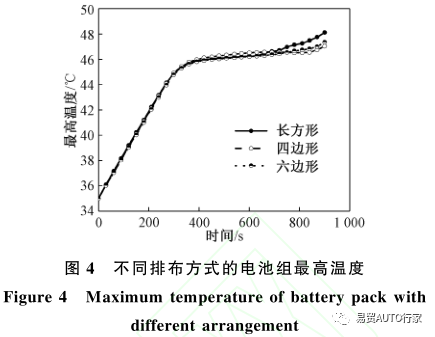
由图4可以看出,在达到PCM的熔点前,3种排布方式的电池组的最高表面温度均以较快的速率上升,在达到熔点后则上升速率迅速放缓,直至600s时,长方形排布的电池组上升速率开始增大并很快超过四边形排布和六边形排布的电池组,放电结束时长方形排布、四边形排布和六边形排布的电池组表面最高温度分别为48.12℃、47.03℃和47.35℃。
由图5中可看出,在300s前,电池组表面温差在3种排布方式下均以一定的速率上升,而在达到峰值后均出现了一定程度的下降。在300~600s时,3种排布方式下温差均保持稳定,而600s后,长方形排布的电池组温差开始上升,而四边形排布和六边形排布的电池组温差依然保持稳定。3种排布下最大温差分别为1.79℃(长方形),1.60℃(四边形)和1.19℃(六边形)。
电池间距对电池温度场分布的影响
将电池以1、2、4和6mm的间距排布,长方形和四边形排布下电池数量为20个,六边形排布下为19个,所以六边形排布总体积为长方形和四边形排布的19/20,以相同的比体积计算得到不同排布方式等效的间距(2d),如表2所示,3种排布方式的电池组俯视图如图 6 所示。
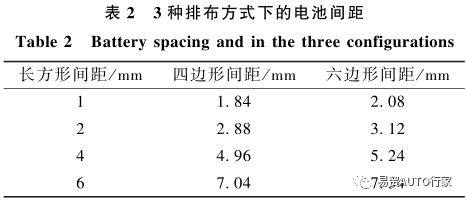
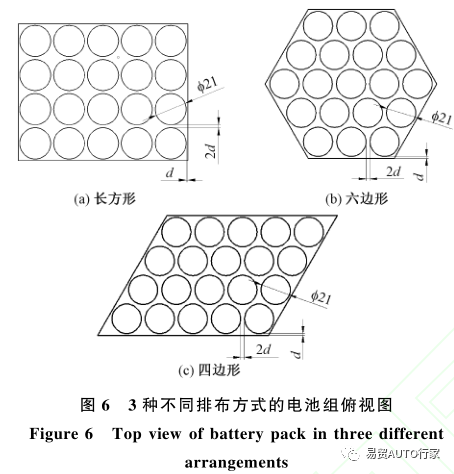
图7为不同间距下3种排布方式电池组的表面最高温度随时间的变化情况。从图7中可以看出,随着电池间距的不断减小,在放电结束时的最高温度不断增大,以长方形排布下的电池组为例,在1、2、4和6mm的间距下,在放电结束时的最高温度分别为49.6、48.4、47.3和46.8℃,且在PCM显热储热阶段的最高温度上升速度也不断增大。同样以长方形排布为例,在1、2、4和6mm的间距下,表面最高温度达到PCM熔点的时间分别为261、266、293和328s。同时也可以看出,不同排布方式下不断减小间距,最高温度的变化幅度也有所不同,在4、6mm的间距下,3种排布方式下的最高温度变化趋势基本相同,而在1、2mm的间距下,长方形排布下电池组的最高温度在放电后期的上升幅度要大于四边形排布和六边形排布的电池组,所以也导致在小间距放电结束时,长方形排布下电池组的最高温度要大于四边形排布和六边形排布,例如在1mm的间距下放电结束时3种排布方式的最高温度分别为49.6℃(长方形)、48.8℃(四边形)和48.5℃(六边形)。
图8为不同间距下3种排布方式下电池组的表面温差随时间的变化情况。
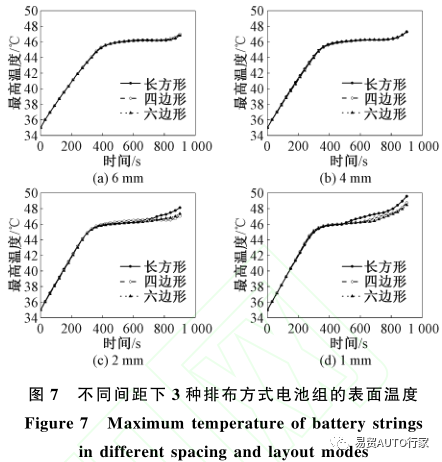
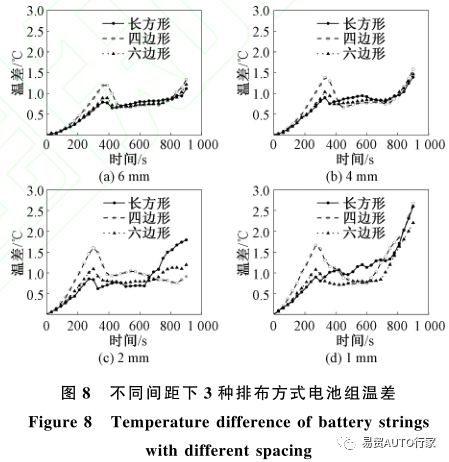
从图8可以看出,在不同间距下,3种排布的电池表面温差在300s前都在不断上升,而四边形排布下的电池组温差上升速率总是要大于其他2种排布方式,在300~600s时,3种排布方式下温差均保持稳定,在600s之后3种排布方式下的温差则又开始上升且随着间距的减少上升速率不断增大。这也导致随着间距的减少,3种排布方式下的温差均不断增大。以四边形排布为例,在1、2、4和6mm的间距下的最大温差分别为2.67、1.60、1.57和1.33℃。
对流换热系数对电池温度场分布的影响
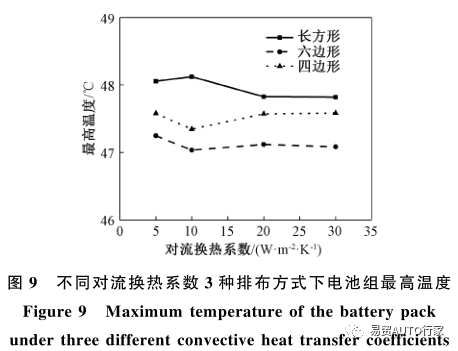
图9为不同对流换热系数下3种排布方式电池组的表面最大温度随时间的变化情况。从图9可以看出,长方形排布电池组的最高温度总是最大而六边形排布的电池组总是最小,随着对流换热系数的变化,3种排布方式下的最高温度并无显著变化。图10为不同对流换热系数下3种排布方式电池组的表面温差随时间的变化情况。
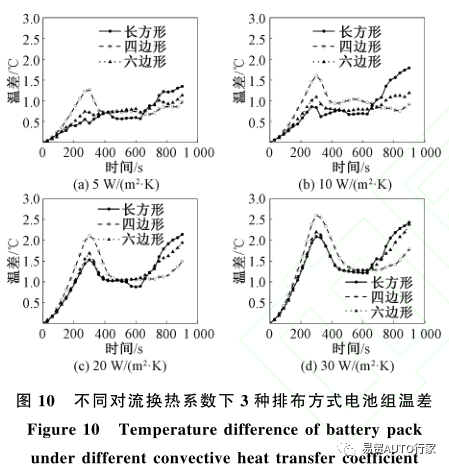
从图10可以看出,随着对流换热系数的增大,在300s前和600s后,温差的上升速率有着明显的上升,其中四边形排布的电池组在300s前上升速率最大而在600s后最小,长方形排布的电池组则与之相反,300s前上升速率最小而在600s后最大,而六边形排布的电池组相较于其他两种排布方式温差波动较小,最大温差也最小。以20W/(m2·K)为例,3种排布方式的最大温差分别为2.14℃(长方形)、2.11℃(四边形)和1.94℃(六边形)。
相变材料导热系数对电池温度场分布的影响
相变材料的导热系数对于PCM热管理系统的性能有着很大的影响,为了研究PCM导热系数对不同排布方式下电池温度场的影响,在模拟中使用导热系数不同其他物性相同的PCM进行计算。
图11为不同导热系数下3种排布方式电池组的表面最大温度随时间的变化情况。3种排布方式下的电池组最大温度有着相同的变化趋势,随着导热系数的不断增大,最高温度不断减小,且减小的速率随着导热系数的增大不断减小。在3种排布方式中,长方形排布的电池组最高温度总是比其他排布方式要高0.5℃左右,而四边形排布和六边形排布电池组的最高温度差距较小,当导热系数小于1W/(m·K)时,六边形的最高温度大于四边形,当导热系数大于1W/(m·K)时,四边形的最高温度大于六边形。
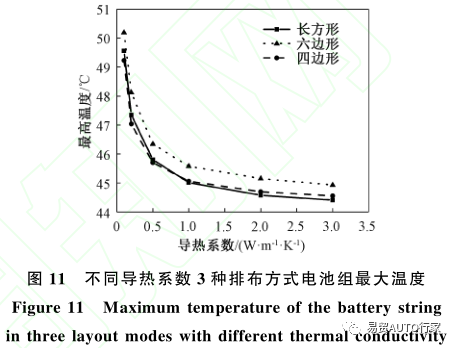
图 12 为不同导热系数下 3 种排布方式电池组的表面温差随时间的变化情况。可以看出随着导热系数的增大,长方形排布和六边形排布下的电池组
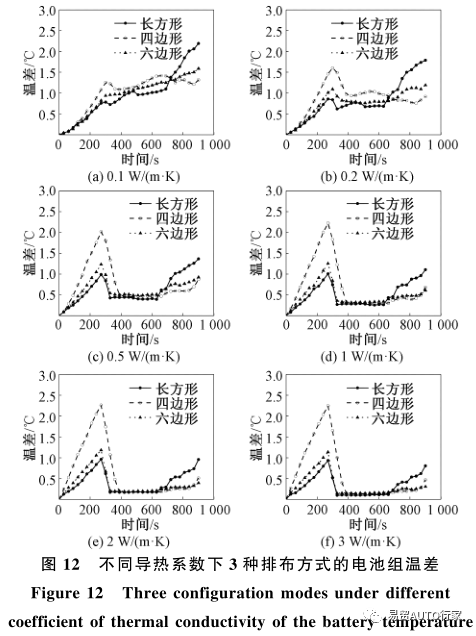
温差在300s前趋势基本没有变化,而在300s后的温差有着明显减小;四边形排布下的电池组在300s前温差随着导热系数的增大不断增大,直至导热系数达到1W/(m·K)时,温差不再上升变化趋势保持不变,在300s后温差有着明显减小。在导热系数大于0.1W/(m·K)时,四边形排布下的电池温差在300s前要明显大于其他2种排布方式,而长方形排布下的电池组温差在600s后要明显大于其他2种排布方式。
03结论
本文以21700锂电池组为研究对象,通过数值模拟的方法研究了电池间距,对流换热系数和PCM导热系数对PCM热管理系统下不同排布方式电池组的温度场影响,得到以下结论:
(1)电池间距大于4mm时,3种排布方式下的电池组最大温度和温差基本相同;小于4mm时,长方形排布的电池组的最高温度最大,六边形排布的电池组最大温差最小,说明排布方式在相变材料不足量时对电池组温度场影响较大。
(2)在不同对流换热系数下,长方形排布的电池组最高温度均为最大,四边形排布均为最小;六边形排布的电池组最大温差均为最小,且随着对流换热系数的增大,最大温差均不断增大,这是由于不同排布方式的热管理系统内部不同位置换热条件不同,而对流换热系数的增大也增大了这一差异。
(3)随着PCM导热系数的增大,3种排布下电池组最高温度均不断减小,长方形排布的电池组最高温度总是最大;3种排布方式的温差在300s后温差均不断减小,在300s前长方形排布和六边形排布的电池组温差无显著变化而四边形排布的电池组温差上升速度则显著增大,直至导热系数达到1W/(m·K)时,温差不再上升变化趋势保持不变。
(4)综合考虑最高温度和温差,采用六边形排布的锂电池组在PCM热管理下的热性能最佳。
审核编辑:汤梓红
-
锂离子电池
+关注
关注
85文章
3264浏览量
78120 -
锂电池
+关注
关注
260文章
8222浏览量
172661 -
PCM
+关注
关注
1文章
198浏览量
53489 -
热管理
+关注
关注
11文章
457浏览量
21958 -
电池
+关注
关注
84文章
10751浏览量
132095
原文标题:电池排布方式对21700锂电池相变热管理系统的影响
文章出处:【微信号:Recycle-Li-Battery,微信公众号:锂电联盟会长】欢迎添加关注!文章转载请注明出处。
发布评论请先 登录
相关推荐
3串锂电池管理,求推荐~求帮助~~
温度对于锂电池包有什么影响?
本公司大量回收汽车退役底盘电池包,电动车锂电池,库存B品锂电池,新能源汽车锂电池时空模组电池包
本公司大量回收汽车退役底盘电池包,回收电动车锂电池,回收库存B品锂电池,回收新能源汽车锂电池
回收锂电池,回收动力电池,回收软包电池,回收动力电池模组,回收圆柱电池,锂电池回收,圆柱电池回收
一个开源的锂电池智能电池管理系统
浅聊21700锂电池的优点与弊端
导热相变化材料在锂电池散热中的应用
导热相变化材料在新能源锂电池散热中的应用
多层次结构的相变材料实现锂电池双重热管理
定制锂电池组的好处?18650锂电池组和21700锂电池组有什么不一样?





 电池排布方式对21700锂电池相变热管理系统的影响
电池排布方式对21700锂电池相变热管理系统的影响











评论