基于优化的多传感器全局位姿估计框架-电子发烧友网

摘要

精确状态估计是自主机器人的基础问题。为了实现局部精确且全局无漂移的状态估计，通常将具有互补性质的多传感器融合到一起。局部传感器（相机、IMU、激光雷达等）在小区域内提供了精确的位姿，而全局传感器（GPS、磁力计、气压计等）在大尺度环境中提供了有噪声但是全局无漂移的定位。在本文中，我们提出一种传感器融合框架将局部状态与全局传感器融合，这实现了局部精确且全局无漂移的位姿估计。由现有的VO/VIO方法产生的局部估计与全局传感器在位姿图优化中融合。在图优化中，局部估计与全局坐标对齐。同时，消除了累积漂移。我们在公开数据集和真实世界实验中评估本文系统的性能。实验结果再次与其它最新的算法进行比较。我们强调，本文系统是一种通用的框架，它能够在统一的位姿图优化中轻易地融合各种全局传感器。我们的实现已经开源。

介绍

在过去几十年中，自主机器人已经成为主流的研究课题。我们已经看到，在自动驾驶、检查、搜索和救援等各种应用中，对机器人的需求越来越迫切。自主任务的基础技术之一为定位。机器人需要精确的6自由度（DoF）位姿进行导航和控制。很多传感器已经被用于局部位姿估计。雷达和激光雷达广泛应用于受限的室内环境，而相机和IMU在室内和室外环境中都适用。

有很多令人印象深刻的算法用于局部位姿估计，例如基于视觉的方法和基于视觉-惯性的方法。这些算法在局部区域内实现了增量式且精确的状态估计。然而，存在一些缺陷限制了这些算法在实际中的使用。局部位姿估计算法的第一个缺陷为，它们在局部坐标系内产生位姿估计（相对于起始点），而不是全局坐标。当我们即使从同一环境中的不同位置开始，我们也可能获得不同的估计结果。因此，如果没有固定的全局坐标，它们对复用是不友好的。第二个缺陷为，由于缺少全局测量数据，在长期运行过程中，局部估计容易累积漂移。

尽管已经提出了一些基于视觉的回环方法来消除漂移，但是它们仍然无法处理带有大量数据的大尺度环境。与局部传感器相比，GPS、气压计、磁力计等全局传感器在大尺度环境中的全局定位方面具有优势。它们提供了相对于固定地球坐标系的全局测量，这是没有漂移的。然而，这些测量信息通常是非平滑且带有噪声的，因此无法直接用于精确控制和导航。以GPS为例，它能够测量以米为单位的近似位置，但是该测量在低频率下是不连续的。此外，它只能测量三维位置，而无法测量三维旋转。

因此，仅有全局传感器是不足以实时地进行6自由度状态估计的。由于局部传感器（相机、IMU和激光雷达）在局部精确性方面实现了令人印象深刻的性能且全局传感器（GPS、磁力计和气压计）是无漂移的，因此聪明的方式是将它们融合到一起以实现局部精确且全局无漂移的6自由度位姿估计。

为了提高鲁棒性，我们想要融合尽可能多的传感器。因此，需要一种支持多传感器的通用框架。尽管传统的基于EKF方法能够逐渐地将局部估计融合到全局坐标系中，但是需要有关不同坐标系之间变换的精确初始值，以保证结果收敛。此外，EKF方法还对时间同步敏感。任何延迟传入的测量数据将导致麻烦，因为无法在滤波过程中反向传递状态。为此，我们使用一种基于优化的方法来解决该问题，它本质上适用于多传感器融合。

在本文中，我们提出一种优化框架来融合局部估计与全局传感器测量。局部估计来自现有的最新VO/VIO工作。全局传感器被作为位姿图中的通用因子。局部传感器和全局传感器因子被累加到一起以构建优化问题。本文系统实现了局部精确且全局无漂移的状态估计。我们强调本文贡献如下： 1）一种通用的框架，将各种全局传感器与局部估计融合，从而实现局部精确且全局无漂移的定位； 2）所提出系统在公开数据集和真实实验中评估； 3）代码对社区开源。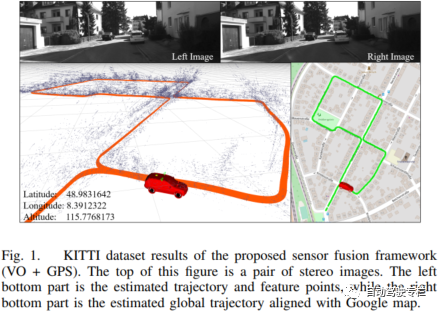

相关工作

最近，状态估计的多传感器融合方法已经成为一种主流趋势，以便提高精度和鲁棒性。根据系统中使用的传感器类型，研究工作能够被分类为局部定位和全局定位。对于局部定位，相机、IMU、激光雷达和RGB-D传感器通常用于小规模环境中进行6自由度状态估计。

过去几十年中令人印象深刻的方法包括基于视觉的方法、基于激光雷达的方法、基于RGB-D的方法和基于事件相机的方法。还有一些多传感器融合方法，例如视觉-惯性融合和视觉-激光雷达融合。在这些工作中，工作A multi-state constraint Kalman filter for vision-aided inertial navigation、High-precision, consistent EKF-based visualinertial odometry和Robust visual inertial odometry using a direct ekf-based approach是基于滤波的方法，而工作Keyframe-based visual-inertial odometry using nonlinear optimization、Visual-inertial monocular slam with map reuse和Vins-mono: A robust and versatilemonocular visual-inertial state estimator是基于优化的方法。在基于优化的框架中，很多视觉测量数据和惯性测量数据被保留在一个捆集中。与观测到的测量值相关的状态被一起优化。

基于优化的方法相比于基于EKF的方法的一个优势在于，状态可以迭代线性化以提高精度。基于滤波的方法和基于优化的方法都可以实现高度精确的状态估计。由于缺少全局测量，累积漂移随着时间是不可避免的。对于全局定位，系统集成了全局传感器（GPS、磁力计、气压计等）。全局传感器测量相对于地球坐标系的绝对量，它们与起点无关。全局测量通常具有噪声且频率较低，所以它们不能够单独使用。所以，全局传感器通常与局部传感器融合，以实现精确且全局的定位。工作A robust and modular multi-sensor fusion approach applied to mav navigation提出一种基于EKF的算法，将视觉测量与惯性和GPS测量相融合，以获得无漂移的估计。工作Multi-sensor fusion for robust autonomous flight in indoor and outdoor environments with a rotorcraft MAV使用无迹卡尔曼滤波（UKF）算法来融合视觉、激光雷达和GPS测量，它是EKF的扩展，其没有解析的雅可比。基于滤波的方法对时间同步很敏感。由于状态无法在滤波过程中反向传递，所以任何延迟传入的测量都会引起麻烦。因此，需要特殊的排序机制来确保来自多个传感器的所有测量数据都是有序的。

与基于滤波的方法相比，基于优化的方法在这方面具有优势。因为大的捆集作为一个天然的缓冲区，它可以等待并且存储很长一段时间的测量值。工作Gomsf: Graph-optimization based multi-sensor fusion for robust uav pose estimation使用一种基于优化的框架来融合局部视觉惯性里程计（VIO）与GPS测量，这比工作A robust and modular multi-sensor fusion approach applied to mav navigation中提出的方法产生了更精确的结果。在该方法中，局部坐标和全局坐标之间的变换被经常优化。很少有研究工作融合超过三种类型的传感器。在本文中，我们提出一种更通用的基于优化的全局定位框架，它可以支持多个全局传感器。每个传感器作为一个通用的因子，其可以很容易地加入到优化问题中。

系统概述

根据测量数据所在的参考系，我们将传感器分类为局部类型和全局类型。

1）局部传感器：相机、激光雷达、IMU（加速度计和陀螺仪）等。这类传感器不是全局参考的，因此通常需要一个参考坐标系。通常，机器人的首个位姿被设置为原点，以便启动传感器。机器人的位姿估计从起点开始增量式地累积。因此，累积漂移将随着距离起点距离的增加而增大。

2）全局传感器：GPS、磁力计、气压计等。这类传感器是全局参考的。它总是在一个固定的全局坐标系（例如地球坐标系）下工作。参考系的原点固定，并且事先是已知的。它们的测量数据是全局但是带有噪声的。其误差与行驶距离无关。对于GPS，它测量相对于地球的绝对经度、维度和高度。精度、维度和高度可以转换为x、y和z坐标。对于磁力计，它测量磁场方向和强度，这可以确定方向。对于气压计，它测量气压，这可以转换成高度。本文框架如图2所示。局部传感器（相机和IMU）被用于局部估计。采用现有的VO/VIO方法来产生局部位姿。局部结果和全局传感器输入到全局位姿图中。它们被转化为统一的因子来构建优化问题。全局估计器生成局部精确且全局的6自由度位姿结果。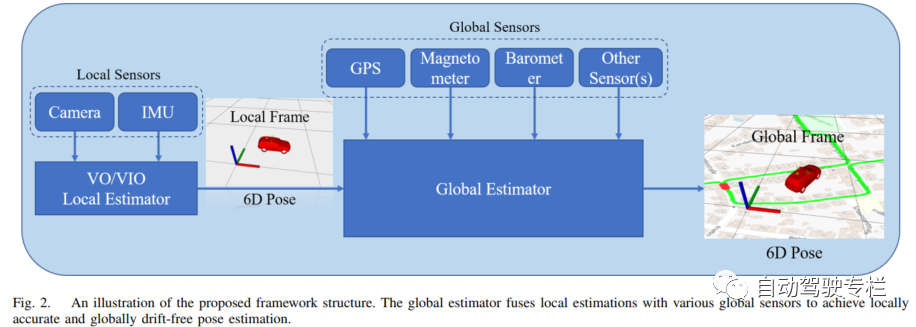

方法

A.局部位姿估计

对于局部位姿估计，我们采用现有的视觉里程计（VO）/视觉-惯性里程计（VIO）算法。有很多令人印象深刻的VO/VIO算法，例如工作Orb-slam: a versatile and accurate monocular slam system、A multi-state constraint Kalman filter for vision-aided inertial navigation和Vins-mono: A robust and versatile monocular visual-inertial state estimator。它们中任何一个可以在本框架中用于局部位姿估计，只要它能产生6自由度位姿。这部分不是本文的主要贡献。出于完整性考虑，本文简要介绍我们先前的VIO算法，其在我们的开源实现中使用。

VIO估计滑动窗口内若干IMU帧的位姿和特征的深度。状态量定义为：

其中，第个IMU状态由IMU中心相对于局部参考系的位置、速度和姿态组成。我们使用四元数来表示姿态。首个IMU位姿被设置为参考帧。和分别为加速度计偏置和陀螺仪偏置。当特征在相机帧中首次被观测到时，使用它们的逆深度进行参数化。估计问题被转换成一个非线性最小二乘问题：

其中，和分别表示惯性和视觉残差。先验项包含关于过去边缘化状态的信息。表示鲁棒huber核。VIO在局部坐标系中实现了精确的实时6自由度位姿估计。

B.全局位姿图结构

全局位姿图结构的图示如图3所示。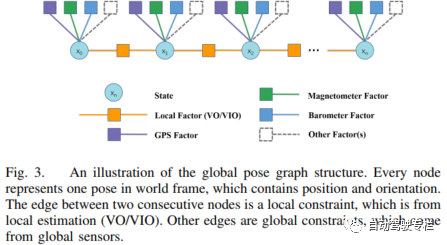

每个位姿包含世界坐标系中位置和姿态，其作为位姿图中一个节点。节点的密度由最低频率的传感器确定。两个连续节点之间的边是一个局部约束，它来自于局部估计（VO/VIO）。该边约束了一个节点到另一个节点的相对位姿。其它边为全局约束，它来自全局传感器。位姿图优化的本质是一个最大似然估计（MLE）问题。MLE由机器人位姿在一段时间上的联合概率分布组成。变量为所有节点全局位姿，，其中，。和为全局坐标系下位置和姿态。在所有测量概率是独立的假设之下，问题通常被推导为：其中，为测量值集合，其包括局部测量（VO/VIO）和全局测量（GPS、磁力计、气压计等）。我们假设测量的不确定性为具有均值和协方差的高斯分布，即。因此，上述方程推导为： Mahalanobis范数为。接着，状态估计转化为非线性最小二乘问题，这也被称为捆集调整（BA）。

C.传感器因子

1）局部因子：由于局部估计（VO/VIO）在小范围区域内是精确的，所以我们利用两帧之间的相对位姿。考虑两个连续帧和帧，局部因子推导为：其中，和为来自VO/VIO的局部帧在时刻和的位姿。为四元数误差状态上的减法操作。第一行表示两个位姿间相对位置误差，第二行表示两个位姿间相对旋转误差。如果VO/VIO算法产生位姿的协方差矩阵，我们使用它作为局部测量的协方差。否则，我们对所有的局部测量使用统一的协方差。

2）GPS因子：GPS的原始测量值为经度、纬度和海拔高度，其不是x、y和z轴坐标。通常，我们可以将经度、纬度和海拔高度转换为地心地固（ECEF）坐标，局部东北天（ENU）坐标和局部北东地（NED）坐标。这里，我们取ENU坐标为例。通过设置首个GPS测量为原点，我们获得ENU世界坐标系中的GPS测量数据，。GPS因子推导为： GPS测量直接约束每个节点的位置。当接收到测量数据时，协方差由卫星的数量确定。当接收到越多卫星信号，协方差就越小。

3）磁力计因子：磁力计可以测量磁场强度的矢量。这个矢量的方向可以帮助确定世界坐标系中的姿态。我们假定磁力计是经过离线标定的，没有偏移或者偏置。首先，我们查表以获得ENU坐标系中局部区域的磁场强度。我们假设磁场强度在这个区域内是恒定的。我们的测量数据表示为。如果我们将传感器与ENU坐标对齐，则的姿态应该与匹配。受此启发，因子推导为：其中，为机器人中心到磁力计中心的变换，这是已知且经过离线标定的。由于磁场容易受到环境影响，我们仅使用没有长度的归一化向量。长度被用于确定协方差。如果测量的长度与相差很大，我们就设置一个大的协方差。否则，我们使用一个小的协方差。

4）气压计因子：气压计测量一个地区的气压。我们假设一段时间内某一海拔高度上的气压是恒定的。因此，气压可以线性地转换为高度。与GPS相同，我们设置首个测量为原始高度。接着，我们获得高度的测量值。直观而言，该因子为高度估计的残差，其写为：由于该测量具有噪声，因此我们计算短时间内若干测量的方差，并且在代价函数中使用它。

5）其它全局因子：尽管我们仅详细说明GPS因子、磁力计因子和气压计因子，但是我们的系统不限于这些全局传感器。本文系统也可以使用其它全局传感器，甚至一些人工传感器（例如运动捕捉系统、WiFi和蓝牙指纹）。关键是将这些测量建模为全局坐标系下的残差因子。

D.位姿图优化

一旦构建了位姿图，优化它等价于寻找尽可能匹配所有边的节点配置。Ceres求解器用于求解该非线性问题，它以迭代的方式利用Gaussian-Newton和Levenberg -Marquadt方法。我们以低频率（1Hz）运行位姿图优化。在每次优化后，我们获得局部坐标系到全局坐标系的变换。因此，我们可以通过这一变换来转换随后的高频局部位姿（VO/VIO，200Hz），以获取实时高频的全局位姿。由于位姿图是相当稀疏的，所以计算复杂度随位姿数量线性增加。我们可以维持一个巨大的窗口进行位姿图优化，以获取精确且全局无漂移的位姿估计。当计算复杂度超过实时能力时，我们丢弃旧的位姿和测量数据，并且将窗口规模维持在有限的尺寸。