Σ-Δ模数转换器：数字滤波器类型

要想理解数字滤波器在Σ-Δ模数转换中如此重要的原因，关键的一点是需要对Σ-Δ调制器有一个基本了解。文中解释了模拟输入信号转变成数字比特流的过程。

当客户在Σ-Δ调制器中绘制量化噪声的频谱时，将看到频率越高时量化噪声越密集。这是Σ-Δ ADC为众人所知的臭名昭著的噪声整形。为了降低量化噪声，客户将调制器输出馈至低通滤波器。

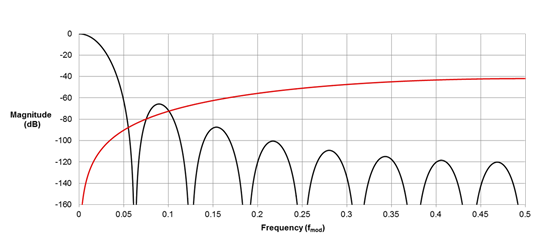
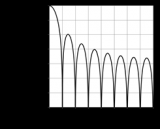
图1所示为在被称为sinc滤波器的Σ-Δ模数转换器中发现的，通过常见的低通数字滤波器响应绘制的量化噪声图（它的名字源于其sin（x）/ x频率响应）。

大小（dB）
	频率（fmod）

图1：Σ-Δ量化噪声和Sinc低通滤波器的频谱

Sinc滤波器，虽然极为常见，但并非Σ-Δ ADC附带的唯一一种数字低通滤波器。例如，有些ADC（如ADS1220）会增加一个额外的50Hz / 60Hz陷波滤波器，用于具有大量电力线干扰的应用。从另一方面讲，ADS127L01具有用于更高频率应用的宽带宽平通带数字滤波器。

正如我的同事Ryan Andrews在其关于抗混叠滤波器的博文中解释道，Σ-Δ ADC中的数字滤波器具有另外一项抽取功能。这些滤波器以低很多的速率（fDR）通过被称为过采样率（OSR）的因子抽取调制器采样频率和输出数据。综合OSR和滤波器类型来确定数字滤波器的输出带宽。大过采样率会产生小型滤波器带宽，从而转化为极好的隔音性能，简化了抗混叠前端，并降低了主机控制器的接口速度。

大多数数字滤波器具有有限脉冲响应（FIR）。这些滤波器本质上是稳定的，易于通过线性相位响应进行设计。让我们来对比Σ-Δ ADC中的两种FIR滤波器。第一种是ADS127L01中的宽带滤波器。第二种是一个典型的三阶正弦响应滤波器，或sinc3。图2和图3并排绘制这些响应。

大小（dB）	频率（fDR）	大小（dB）	频率（fDR）
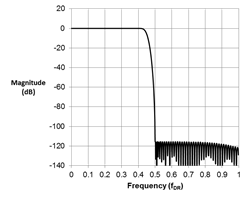
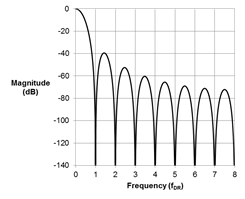
图2：宽带滤波器的频率响应		图3：Sinc3的频率响应

很快，客户可以清楚地看到在交流（AC）测量应用中使用宽带滤波器的优点。数据率（fDR/2）的奈奎斯特带宽之前其近0 dB的增益确保了在通带频率上不会出现信号功率损耗。急剧升降的过渡带限制了混叠。另一方面，sinc3滤波器通过0.262 x fDR及fDR/2之后的缓慢过渡，将信号衰减至-3dB，这样会将更多的带外噪声调入相关的带宽。表面上看，宽带FIR滤波器将是任何应用的理想选择；然而，要想获得这一出色的频域性能需要付出代价。

宽带滤波器和sinc滤波器之间的权衡在于时域。宽带滤波器是一个非常高阶的滤波器，这说明它在收到一个阶跃输入后，需要花费很长时间才能得出一个最终值。在ADS127L01的宽带滤波器中，客户将不得不等待84次转换才能收到一个固定输出。输入处出现一次阶跃后，sinc3滤波器会通过三次转换固定下来，让客户通过多个传感器进行循环。所有FIR滤波器都需要在频率响应和延迟之间进行权衡。

审核编辑：郭婷