电磁场和复数有什么关系？

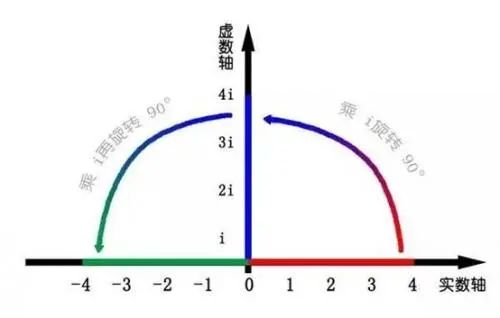
众所周知，复数，是数的概念扩展。我们把形如z=a+bi（a、b均为实数）的数称为复数。其中，a称为实部，b称为虚部，i称为虚数单位。这个概念是不是非常熟悉，这是几乎每个人中学时代都学过的一个数学概念，复数最直观的理解就是旋转！4*i*i = -4就是“4”在数轴上旋转了 180 度。那么 4*i 就是旋转了 90 度。

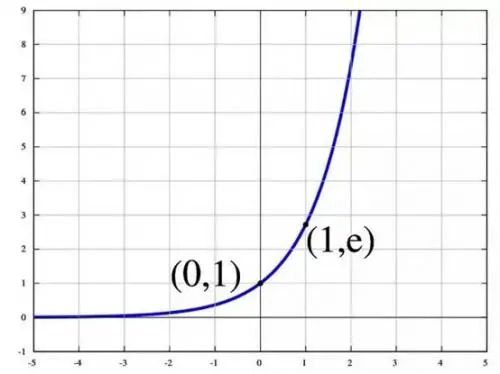
另外，e^t 是什么样呢？

但当你在指数上加上 i 之后呢？

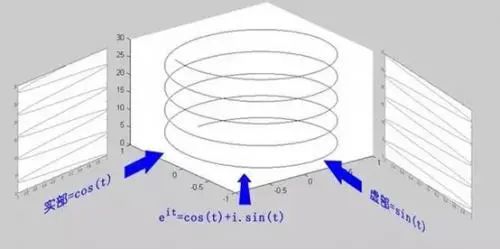
变成了一个螺旋线。是不是和电磁场很像？（想拿欧拉公式去跟女生炫学术的男生注意了：她们，真的，不 CARE）

当然，更重要的意义在于复数运算保留了二维信息。

假如我让你计算 3+5，虽然你可以轻松的计算出 8，但是如果让你分解 8 你会有无数种分解的方法，3 和 5 原始在各自维度上的信息被覆盖了。

但是计算 3+5i 的话，你依然可以分解出实部和虚部，就像上图那样。

基于以上两个理由，用复数来描述电场与磁场简直完美到爆棚！

我们即可以让电场强度与复数磁场强度相加而不损失各自的信息，又满足了电场与磁场 90 度垂直的要求。另外，一旦我们需要让任何一个场旋转 90 度，只要乘一个“i”就可以了。

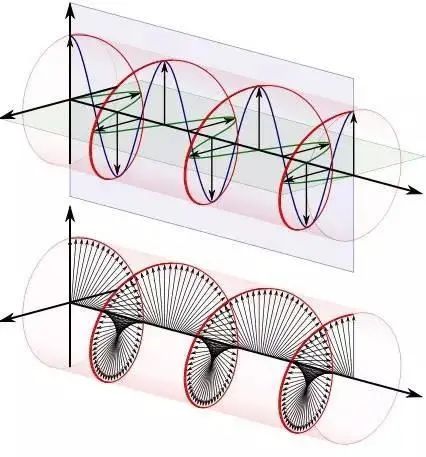
补充一点：正弦波在频域可以看作是自然数中的“1”，可以构成其他数字的基础元素。当你需要 5 的时候，你可以看成是 1*5（基础元素的五倍）也看以看成 2+3（一个基础元素 2 倍与基础元素 3 倍的和）。这些用基础元素构成新元素的运算是线性运算。但是现在你如何用线性运算吧 2sin（wt）变换成 4sin（wt+pi/6）呢？利用欧拉公式，我们可以将任何一个正弦波看作其在实轴上的投影。假如两个不同的正弦波，可以用数学表达为

好了，现在如果我想用第一个正弦波利用线性变换为第二个，我们就只需要将 A 乘对应的系数使其放大至 B（本例为乘 2），然后将θ1 加上一定的角度使其变为θ2（本例为加 30 度），然后将得到的第二个虚数重新投影回实轴，就完成了在实数中完全无法做到的变换。

这种利用复指数来计算正弦波的方法也对电磁波极其适用，因为电磁波都是正弦波，当我们需要一个电磁波在时间上延迟 / 提前，或是在空间上前移 / 后移，只需要乘一个复指数就可以完成对相位的调整了，总体上来说还是比较实用的。

审核编辑：汤梓红