01前言伯克利的马毅教授在线上开展了为期 2 周的暑期课程,课程主讲 3D视觉,课程涉及内容十分丰富,受限于版权原因可能不会公开,所有内容都可以在马老师的«An invitation to 3D vision»一书中进行深入了解。本篇博客重点解读 Two View Geometry 的部分内容,这也是马老师重点强调的内容。其实这部分内容在大多数课程和教材中都有涉及,很多人可能也觉得很简单,有一定的套路可言,但是如标题所说,你真的理解Two View Geometry吗?笔者曾面试过 DJI 以及 Nreal 两家很棒的公司,面试时都问到了这一部分,当时还觉得自己答得不错,但是听过马老师的课程之后发现,其实我也并不是很了解 Two View Geometry。接下来我会依据马老师的课件以及教材详细介绍 Two View Geometry, 在这之后的下一篇博客我会介绍一篇 CVPR 2021 的工作 Deep Two-View Structure-from-Motion Revisited,下面进入正式内容。02Traditional Two View Geometry下面这张图是一个 Geometric Vision 的简略回顾: 大致历程是:从双视图,到三视图四视图,再到统一的多视图。内容我们只涉及双视图的,按照书中的标题来说就是:Reconstruction from Two Calibrated Views. 所要做的事情就是,给定两张同一场景不同视角下拍摄到的图像,恢复出相机的位姿以及场景的结构。
大致历程是:从双视图,到三视图四视图,再到统一的多视图。内容我们只涉及双视图的,按照书中的标题来说就是:Reconstruction from Two Calibrated Views. 所要做的事情就是,给定两张同一场景不同视角下拍摄到的图像,恢复出相机的位姿以及场景的结构。 我们假设先前的预备工作已经准备充分,相机已经标定完成,correspondence 也已经匹配完成,那么不失一般性的可以用下面这个等式来进行表述:
我们假设先前的预备工作已经准备充分,相机已经标定完成,correspondence 也已经匹配完成,那么不失一般性的可以用下面这个等式来进行表述: 这里
这里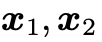 分别表示视角1以及视角2下,对空间中同一个点的观测,这里是使用归一化平面坐标进行表达,
分别表示视角1以及视角2下,对空间中同一个点的观测,这里是使用归一化平面坐标进行表达,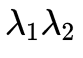 表示
表示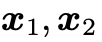 对应的深度值,
对应的深度值,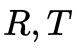 表示从视角 1 到视角 2 的 Rigid Body Motion。所谓恢复 motion 以及 structure 就是计算深度
表示从视角 1 到视角 2 的 Rigid Body Motion。所谓恢复 motion 以及 structure 就是计算深度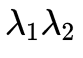 以及变换
以及变换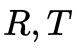 。(1)式在有多次观测时,
。(1)式在有多次观测时,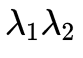 是一直变化的,而相机运动
是一直变化的,而相机运动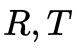 却是始终不变的,为了追求统一,虽然说法有些哲学(玄学),但是道理就是这么个道理,我们需要同时叉乘T,消去场景结构带来的影响,然后就得到了著名的Epipolar Geometry:
却是始终不变的,为了追求统一,虽然说法有些哲学(玄学),但是道理就是这么个道理,我们需要同时叉乘T,消去场景结构带来的影响,然后就得到了著名的Epipolar Geometry: 我们把
我们把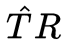 这个矩阵用
这个矩阵用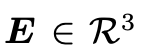 表示,并称之为Essential matrix. 这是Longuet-Higgins 在 1981 年发现的,感谢前人贡献。正如推导过程所阐述的,(2)式只与相机的运动有关, right?并且因为(2)式右边为0,说明这是一个齐次等式,乘以任意的常数依然正确,而
表示,并称之为Essential matrix. 这是Longuet-Higgins 在 1981 年发现的,感谢前人贡献。正如推导过程所阐述的,(2)式只与相机的运动有关, right?并且因为(2)式右边为0,说明这是一个齐次等式,乘以任意的常数依然正确,而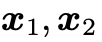 是观测,
是观测,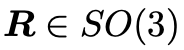 ,因此常数只能给
,因此常数只能给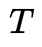 ,这也符合我们的常识,即单目相机没有办法恢复尺度。但是没有关系,we only care about the direction!对极几何还表达了一个重要的属性就是3点共面,
,这也符合我们的常识,即单目相机没有办法恢复尺度。但是没有关系,we only care about the direction!对极几何还表达了一个重要的属性就是3点共面,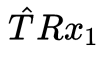 表示了这个平面的法向量,right?所以在什么情况下,法向量与
表示了这个平面的法向量,right?所以在什么情况下,法向量与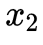 点乘为0呢?只能是共面。可以看到,代数与几何是统一的,你甚至可以直接根据几何写出(2)式。对极几何的表达十分简洁,并且有许多有趣的性质:
点乘为0呢?只能是共面。可以看到,代数与几何是统一的,你甚至可以直接根据几何写出(2)式。对极几何的表达十分简洁,并且有许多有趣的性质: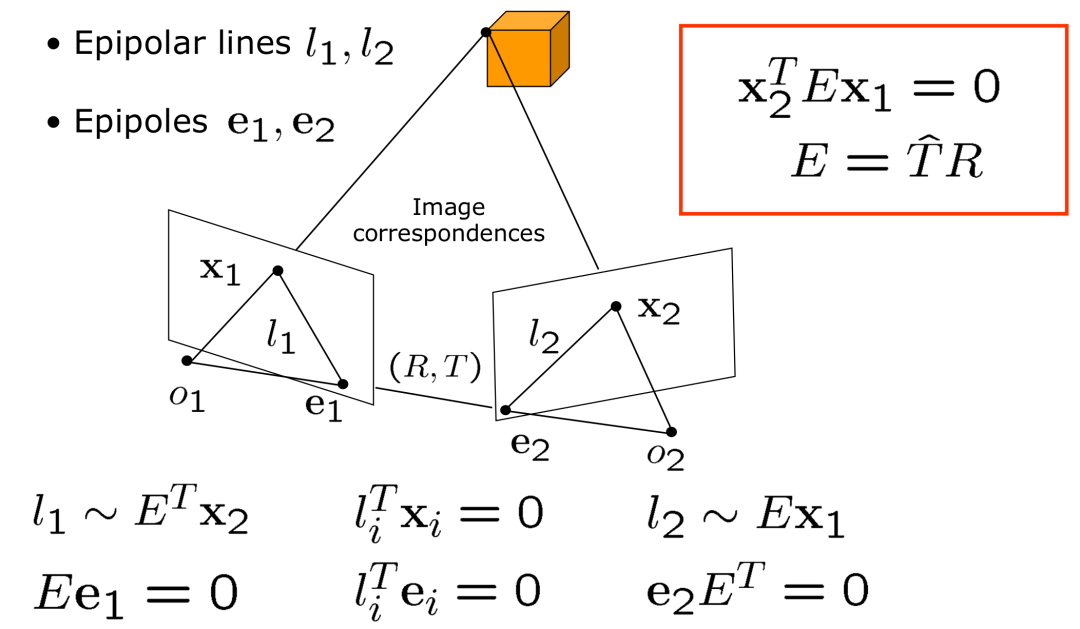 我们来稍加解读。按照上面的说法,对极几何其实表达的是三点共面,
我们来稍加解读。按照上面的说法,对极几何其实表达的是三点共面,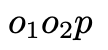 三个点会形成一个三角形,从而确定一个平面,不论空间点
三个点会形成一个三角形,从而确定一个平面,不论空间点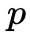 怎么变,
怎么变,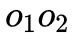 这条边是不变的。在几何层面,线和面不平行就会产生交点,我们称成像平面与
这条边是不变的。在几何层面,线和面不平行就会产生交点,我们称成像平面与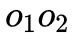 的交点为
的交点为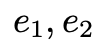 Epipoles:
Epipoles: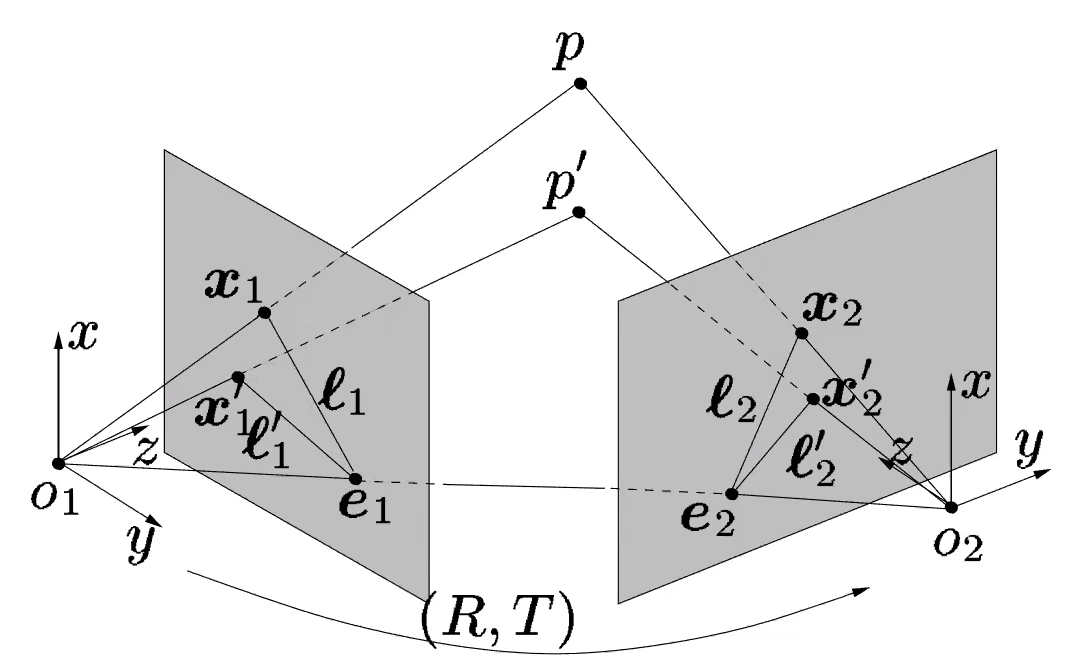 类似的你可以了解 Epipolar line 的定义。具体的性质可以参考马老师的书,这里我简单描述一下,
类似的你可以了解 Epipolar line 的定义。具体的性质可以参考马老师的书,这里我简单描述一下,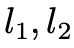 是极线,但是我们选择用三角形平面的法向量去描述极线,因为法向量确定了极线就唯一确定了。剩下的挨个理一下就通了。接下来难度会提升一些。对极几何很美,如何解呢?这个方程是 homo- geneous 的,因此E的自由度为最多为 8,事实上我们知道实际自由度是 5(旋转矩阵的自由度为 3,不考虑尺度因素,平移向量的自由度为 2),但是暂且不考虑这个。因此如果给定8对 correspondence(这里我们不考虑共线共面以及其他的corner case),至少E可以解出。接下来会面对两个问题:1.
是极线,但是我们选择用三角形平面的法向量去描述极线,因为法向量确定了极线就唯一确定了。剩下的挨个理一下就通了。接下来难度会提升一些。对极几何很美,如何解呢?这个方程是 homo- geneous 的,因此E的自由度为最多为 8,事实上我们知道实际自由度是 5(旋转矩阵的自由度为 3,不考虑尺度因素,平移向量的自由度为 2),但是暂且不考虑这个。因此如果给定8对 correspondence(这里我们不考虑共线共面以及其他的corner case),至少E可以解出。接下来会面对两个问题:1. 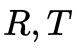 怎么解呢?2.假设你知道怎么解出
怎么解呢?2.假设你知道怎么解出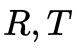 ,而实际应用中,我们的correspondence都是很noise的,这样得到的解也是带噪声的,那么如何把噪声去掉,得到一个干干净净的Essential Matrix呢?带着这些问题继续往下走。我们通过8个点对,解出的矩阵记作
,而实际应用中,我们的correspondence都是很noise的,这样得到的解也是带噪声的,那么如何把噪声去掉,得到一个干干净净的Essential Matrix呢?带着这些问题继续往下走。我们通过8个点对,解出的矩阵记作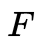 ,首先有一点你要了解,不是任何3×3的矩阵都能分解为
,首先有一点你要了解,不是任何3×3的矩阵都能分解为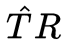 这种形式的,
这种形式的,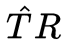 的自由度是6,如果upto scale的话,自由度则是5,并且包含一个
的自由度是6,如果upto scale的话,自由度则是5,并且包含一个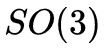 的旋转矩阵部分,因此
的旋转矩阵部分,因此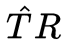 也是一个 special group,有其对应的空间(essential space),或者说 5 维的流形上(essential manifold),当有噪声时,得到的解
也是一个 special group,有其对应的空间(essential space),或者说 5 维的流形上(essential manifold),当有噪声时,得到的解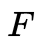 会在这个空间外。为了便于表达,我们引入 normalized essential matrix 来消除尺度的干扰:
会在这个空间外。为了便于表达,我们引入 normalized essential matrix 来消除尺度的干扰: 在后文我们提到的
在后文我们提到的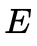 不特殊说明都指的是normalized essential matrix.我们希望能在 essential space 中找到一个距离F最“近”的解,然后将F投影到这个解上,如下图所示:
不特殊说明都指的是normalized essential matrix.我们希望能在 essential space 中找到一个距离F最“近”的解,然后将F投影到这个解上,如下图所示: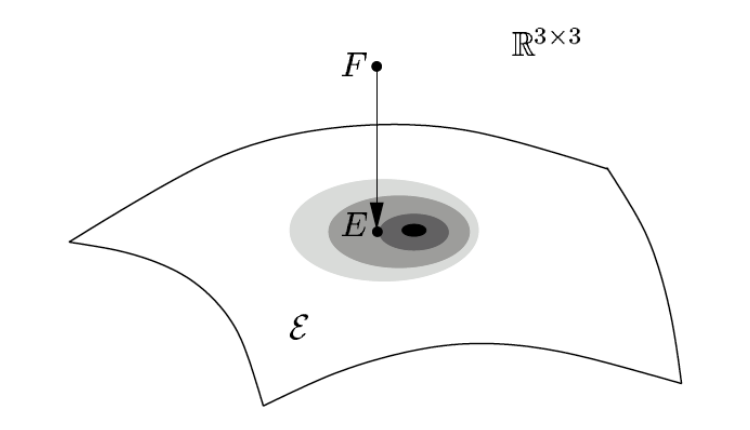 在说明怎样投影前,我们需要先给出三个定理:
在说明怎样投影前,我们需要先给出三个定理: 定理一描述了一个矩阵为 Essential Matrix 的充要条件。
定理一描述了一个矩阵为 Essential Matrix 的充要条件。 定理二描述了如何从 Essential Matrix 恢复到旋转矩阵以及平移方向向量。这里需要注意的是,normalized essential matrix 可以消除尺度的干扰,但是不能消除符号的干扰,代数角度而言,E 和−E 都满足Epipolar Constraint,因此实际我们能得到四组解。
定理二描述了如何从 Essential Matrix 恢复到旋转矩阵以及平移方向向量。这里需要注意的是,normalized essential matrix 可以消除尺度的干扰,但是不能消除符号的干扰,代数角度而言,E 和−E 都满足Epipolar Constraint,因此实际我们能得到四组解。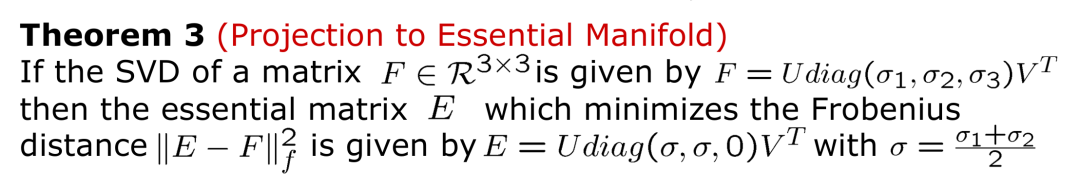 定理三给出了投影的方法,我们选择F-norm作为投影距离的度量指标。这里需要注意的是,
定理三给出了投影的方法,我们选择F-norm作为投影距离的度量指标。这里需要注意的是,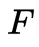 的SVD分解得到的
的SVD分解得到的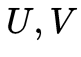 只满足正交性,不能满足行列式为+1的条件,当得到的
只满足正交性,不能满足行列式为+1的条件,当得到的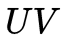 行列式为−1时,我们会对其取负,在后面我们会用代码具体解释。以上三个定理在马老师的书里都有详细证明,出于易读性的考虑后续会单独的整理到我的知乎上分享。在有了这三个定理之后,整个算法也就明朗了,流程如下:
行列式为−1时,我们会对其取负,在后面我们会用代码具体解释。以上三个定理在马老师的书里都有详细证明,出于易读性的考虑后续会单独的整理到我的知乎上分享。在有了这三个定理之后,整个算法也就明朗了,流程如下: 以上就是著名的八点法,你可以在许多资料上看到这个过程,本文的主要目的是梳理八点法的一些思路。我们引用一段 colmap 中的源码来解读上述过程:
以上就是著名的八点法,你可以在许多资料上看到这个过程,本文的主要目的是梳理八点法的一些思路。我们引用一段 colmap 中的源码来解读上述过程: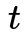 取
取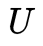 的最后一行可以留给读者作为一个思考题,提示是
的最后一行可以留给读者作为一个思考题,提示是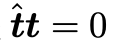 ,然后分析一下矩阵的秩。八点法十分简洁(当然证明过程比较复杂),但是在实际使用过程中,还是会遇到许多问题的,我们在以下简要列举:1. Number of points. 由于 Normalized Essential Matrix 的自由度为 5,在比较 general 的情况下,最少选取的 correspondence 点对为 5(Kruppa在 1913 年的时候给出了五点法,类似八点法会产生 4 个满足对极约束的解,五点法会产生 10个解),因此选取多少点是一个需要实际使用中考虑的问题。2. Number of solutions and positive depth constraint.虽然八点法给出了四对解,但是实际上只有一个正确解,那么其他三个解怎么排除呢?首先从代数层面,不要忘了最原始的表达式
,然后分析一下矩阵的秩。八点法十分简洁(当然证明过程比较复杂),但是在实际使用过程中,还是会遇到许多问题的,我们在以下简要列举:1. Number of points. 由于 Normalized Essential Matrix 的自由度为 5,在比较 general 的情况下,最少选取的 correspondence 点对为 5(Kruppa在 1913 年的时候给出了五点法,类似八点法会产生 4 个满足对极约束的解,五点法会产生 10个解),因此选取多少点是一个需要实际使用中考虑的问题。2. Number of solutions and positive depth constraint.虽然八点法给出了四对解,但是实际上只有一个正确解,那么其他三个解怎么排除呢?首先从代数层面,不要忘了最原始的表达式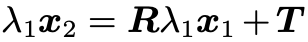 ,在这个表达式中隐藏了一个很关键的约束,深度值应该为正,至于怎么求深度值是三角化部分的知识了,我们不在这里讨论,如果你对上述过程熟悉,不难发现就是一个叉乘的技巧。基于这一约束我们可以将正确的解筛选出来。而从几何层面来看,就是下面这张图(From Multiple View Geometry in Computer Vision):
,在这个表达式中隐藏了一个很关键的约束,深度值应该为正,至于怎么求深度值是三角化部分的知识了,我们不在这里讨论,如果你对上述过程熟悉,不难发现就是一个叉乘的技巧。基于这一约束我们可以将正确的解筛选出来。而从几何层面来看,就是下面这张图(From Multiple View Geometry in Computer Vision):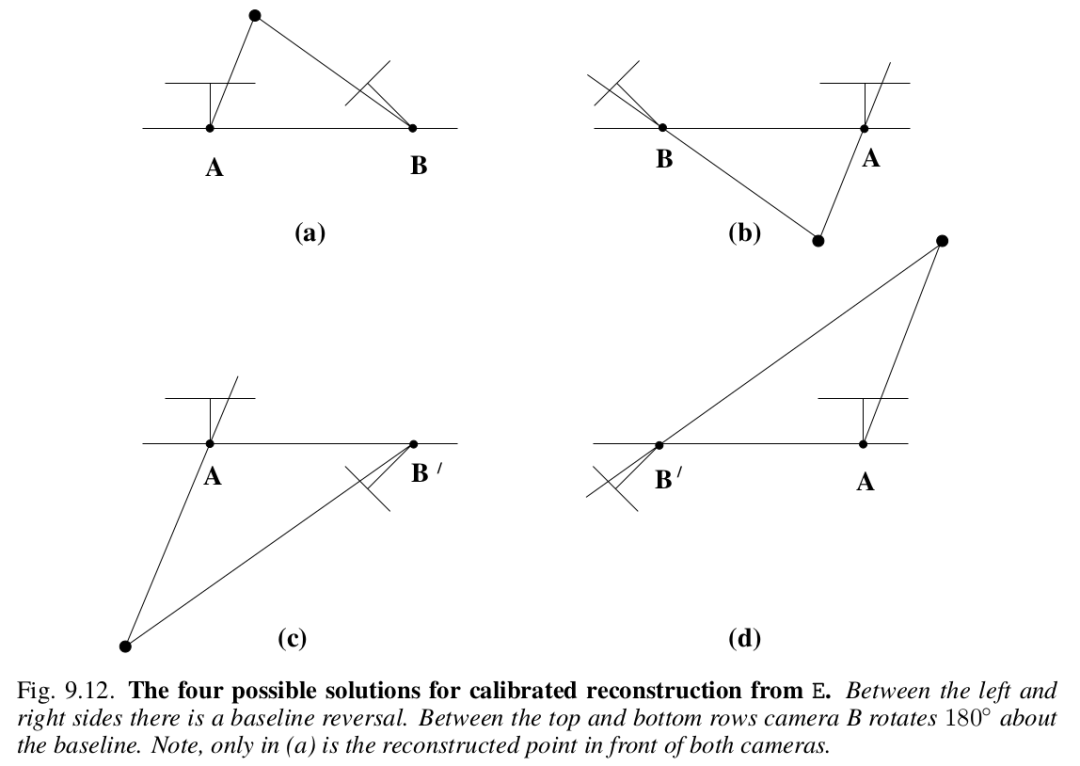 3. Structure requirement: general position.当观测到的空间点满足某些导致退化的条件时(called critical surfaces),使用八点法会遇到解不唯一的情况。一个典型的例子就是观测点共面的情况,这种时候我们需要使用homography 来解决。4. Motion requirement: sufficient parallax.也就是说,平移量不能为0(为0时也要使用 homography)。需要十分小心的是,在没有平移移动且匹配十分 noise 的时候,八点法依旧会得到一个很奇怪的平移部分的解,而这个解是毫无意义的。5. Multiple motion hypotheses.运动物体场景,这又是另一个问题了。03结语Essential Matrix 之所以叫 Essential Matrix,就是因为它太重要了, 马老师花了4节课的时间,介绍two view geometry的内容, 可见其重要性。目前学术的研究主要在于recognition的问题了,也有许多工作还是聚焦在end to end的执着,当然这只是我个人的一些粗浅的看法。审核编辑 :李倩
3. Structure requirement: general position.当观测到的空间点满足某些导致退化的条件时(called critical surfaces),使用八点法会遇到解不唯一的情况。一个典型的例子就是观测点共面的情况,这种时候我们需要使用homography 来解决。4. Motion requirement: sufficient parallax.也就是说,平移量不能为0(为0时也要使用 homography)。需要十分小心的是,在没有平移移动且匹配十分 noise 的时候,八点法依旧会得到一个很奇怪的平移部分的解,而这个解是毫无意义的。5. Multiple motion hypotheses.运动物体场景,这又是另一个问题了。03结语Essential Matrix 之所以叫 Essential Matrix,就是因为它太重要了, 马老师花了4节课的时间,介绍two view geometry的内容, 可见其重要性。目前学术的研究主要在于recognition的问题了,也有许多工作还是聚焦在end to end的执着,当然这只是我个人的一些粗浅的看法。审核编辑 :李倩
 大致历程是:从双视图,到三视图四视图,再到统一的多视图。内容我们只涉及双视图的,按照书中的标题来说就是:Reconstruction from Two Calibrated Views. 所要做的事情就是,给定两张同一场景不同视角下拍摄到的图像,恢复出相机的位姿以及场景的结构。
大致历程是:从双视图,到三视图四视图,再到统一的多视图。内容我们只涉及双视图的,按照书中的标题来说就是:Reconstruction from Two Calibrated Views. 所要做的事情就是,给定两张同一场景不同视角下拍摄到的图像,恢复出相机的位姿以及场景的结构。 我们假设先前的预备工作已经准备充分,相机已经标定完成,correspondence 也已经匹配完成,那么不失一般性的可以用下面这个等式来进行表述:
我们假设先前的预备工作已经准备充分,相机已经标定完成,correspondence 也已经匹配完成,那么不失一般性的可以用下面这个等式来进行表述: 这里
这里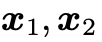 分别表示视角1以及视角2下,对空间中同一个点的观测,这里是使用归一化平面坐标进行表达,
分别表示视角1以及视角2下,对空间中同一个点的观测,这里是使用归一化平面坐标进行表达,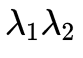 表示
表示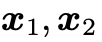 对应的深度值,
对应的深度值,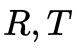 表示从视角 1 到视角 2 的 Rigid Body Motion。所谓恢复 motion 以及 structure 就是计算深度
表示从视角 1 到视角 2 的 Rigid Body Motion。所谓恢复 motion 以及 structure 就是计算深度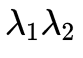 以及变换
以及变换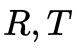 。(1)式在有多次观测时,
。(1)式在有多次观测时,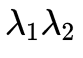 是一直变化的,而相机运动
是一直变化的,而相机运动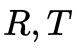 却是始终不变的,为了追求统一,虽然说法有些哲学(玄学),但是道理就是这么个道理,我们需要同时叉乘T,消去场景结构带来的影响,然后就得到了著名的Epipolar Geometry:
却是始终不变的,为了追求统一,虽然说法有些哲学(玄学),但是道理就是这么个道理,我们需要同时叉乘T,消去场景结构带来的影响,然后就得到了著名的Epipolar Geometry: 我们把
我们把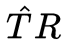 这个矩阵用
这个矩阵用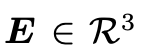 表示,并称之为Essential matrix. 这是Longuet-Higgins 在 1981 年发现的,感谢前人贡献。正如推导过程所阐述的,(2)式只与相机的运动有关, right?并且因为(2)式右边为0,说明这是一个齐次等式,乘以任意的常数依然正确,而
表示,并称之为Essential matrix. 这是Longuet-Higgins 在 1981 年发现的,感谢前人贡献。正如推导过程所阐述的,(2)式只与相机的运动有关, right?并且因为(2)式右边为0,说明这是一个齐次等式,乘以任意的常数依然正确,而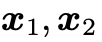 是观测,
是观测,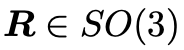 ,因此常数只能给
,因此常数只能给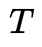 ,这也符合我们的常识,即单目相机没有办法恢复尺度。但是没有关系,we only care about the direction!对极几何还表达了一个重要的属性就是3点共面,
,这也符合我们的常识,即单目相机没有办法恢复尺度。但是没有关系,we only care about the direction!对极几何还表达了一个重要的属性就是3点共面,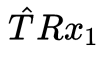 表示了这个平面的法向量,right?所以在什么情况下,法向量与
表示了这个平面的法向量,right?所以在什么情况下,法向量与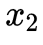 点乘为0呢?只能是共面。可以看到,代数与几何是统一的,你甚至可以直接根据几何写出(2)式。对极几何的表达十分简洁,并且有许多有趣的性质:
点乘为0呢?只能是共面。可以看到,代数与几何是统一的,你甚至可以直接根据几何写出(2)式。对极几何的表达十分简洁,并且有许多有趣的性质: 我们来稍加解读。按照上面的说法,对极几何其实表达的是三点共面,
我们来稍加解读。按照上面的说法,对极几何其实表达的是三点共面,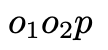 三个点会形成一个三角形,从而确定一个平面,不论空间点
三个点会形成一个三角形,从而确定一个平面,不论空间点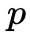 怎么变,
怎么变,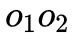 这条边是不变的。在几何层面,线和面不平行就会产生交点,我们称成像平面与
这条边是不变的。在几何层面,线和面不平行就会产生交点,我们称成像平面与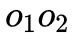 的交点为
的交点为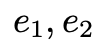 Epipoles:
Epipoles: 类似的你可以了解 Epipolar line 的定义。具体的性质可以参考马老师的书,这里我简单描述一下,
类似的你可以了解 Epipolar line 的定义。具体的性质可以参考马老师的书,这里我简单描述一下,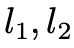 是极线,但是我们选择用三角形平面的法向量去描述极线,因为法向量确定了极线就唯一确定了。剩下的挨个理一下就通了。接下来难度会提升一些。对极几何很美,如何解呢?这个方程是 homo- geneous 的,因此E的自由度为最多为 8,事实上我们知道实际自由度是 5(旋转矩阵的自由度为 3,不考虑尺度因素,平移向量的自由度为 2),但是暂且不考虑这个。因此如果给定8对 correspondence(这里我们不考虑共线共面以及其他的corner case),至少E可以解出。接下来会面对两个问题:1.
是极线,但是我们选择用三角形平面的法向量去描述极线,因为法向量确定了极线就唯一确定了。剩下的挨个理一下就通了。接下来难度会提升一些。对极几何很美,如何解呢?这个方程是 homo- geneous 的,因此E的自由度为最多为 8,事实上我们知道实际自由度是 5(旋转矩阵的自由度为 3,不考虑尺度因素,平移向量的自由度为 2),但是暂且不考虑这个。因此如果给定8对 correspondence(这里我们不考虑共线共面以及其他的corner case),至少E可以解出。接下来会面对两个问题:1. 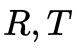 怎么解呢?2.假设你知道怎么解出
怎么解呢?2.假设你知道怎么解出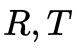 ,而实际应用中,我们的correspondence都是很noise的,这样得到的解也是带噪声的,那么如何把噪声去掉,得到一个干干净净的Essential Matrix呢?带着这些问题继续往下走。我们通过8个点对,解出的矩阵记作
,而实际应用中,我们的correspondence都是很noise的,这样得到的解也是带噪声的,那么如何把噪声去掉,得到一个干干净净的Essential Matrix呢?带着这些问题继续往下走。我们通过8个点对,解出的矩阵记作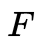 ,首先有一点你要了解,不是任何3×3的矩阵都能分解为
,首先有一点你要了解,不是任何3×3的矩阵都能分解为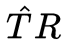 这种形式的,
这种形式的,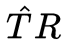 的自由度是6,如果upto scale的话,自由度则是5,并且包含一个
的自由度是6,如果upto scale的话,自由度则是5,并且包含一个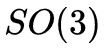 的旋转矩阵部分,因此
的旋转矩阵部分,因此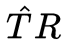 也是一个 special group,有其对应的空间(essential space),或者说 5 维的流形上(essential manifold),当有噪声时,得到的解
也是一个 special group,有其对应的空间(essential space),或者说 5 维的流形上(essential manifold),当有噪声时,得到的解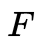 会在这个空间外。为了便于表达,我们引入 normalized essential matrix 来消除尺度的干扰:
会在这个空间外。为了便于表达,我们引入 normalized essential matrix 来消除尺度的干扰: 在后文我们提到的
在后文我们提到的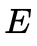 不特殊说明都指的是normalized essential matrix.我们希望能在 essential space 中找到一个距离F最“近”的解,然后将F投影到这个解上,如下图所示:
不特殊说明都指的是normalized essential matrix.我们希望能在 essential space 中找到一个距离F最“近”的解,然后将F投影到这个解上,如下图所示: 在说明怎样投影前,我们需要先给出三个定理:
在说明怎样投影前,我们需要先给出三个定理: 定理一描述了一个矩阵为 Essential Matrix 的充要条件。
定理一描述了一个矩阵为 Essential Matrix 的充要条件。 定理二描述了如何从 Essential Matrix 恢复到旋转矩阵以及平移方向向量。这里需要注意的是,normalized essential matrix 可以消除尺度的干扰,但是不能消除符号的干扰,代数角度而言,E 和−E 都满足Epipolar Constraint,因此实际我们能得到四组解。
定理二描述了如何从 Essential Matrix 恢复到旋转矩阵以及平移方向向量。这里需要注意的是,normalized essential matrix 可以消除尺度的干扰,但是不能消除符号的干扰,代数角度而言,E 和−E 都满足Epipolar Constraint,因此实际我们能得到四组解。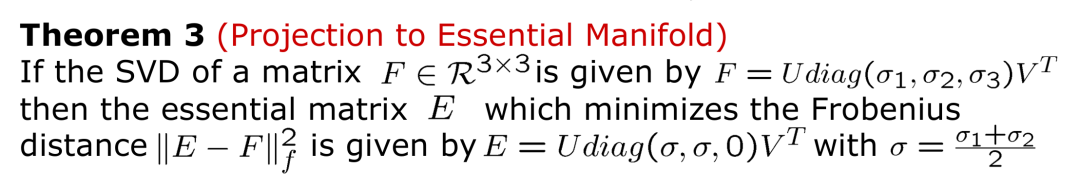 定理三给出了投影的方法,我们选择F-norm作为投影距离的度量指标。这里需要注意的是,
定理三给出了投影的方法,我们选择F-norm作为投影距离的度量指标。这里需要注意的是,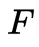 的SVD分解得到的
的SVD分解得到的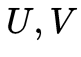 只满足正交性,不能满足行列式为+1的条件,当得到的
只满足正交性,不能满足行列式为+1的条件,当得到的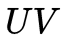 行列式为−1时,我们会对其取负,在后面我们会用代码具体解释。以上三个定理在马老师的书里都有详细证明,出于易读性的考虑后续会单独的整理到我的知乎上分享。在有了这三个定理之后,整个算法也就明朗了,流程如下:
行列式为−1时,我们会对其取负,在后面我们会用代码具体解释。以上三个定理在马老师的书里都有详细证明,出于易读性的考虑后续会单独的整理到我的知乎上分享。在有了这三个定理之后,整个算法也就明朗了,流程如下: 以上就是著名的八点法,你可以在许多资料上看到这个过程,本文的主要目的是梳理八点法的一些思路。我们引用一段 colmap 中的源码来解读上述过程:
以上就是著名的八点法,你可以在许多资料上看到这个过程,本文的主要目的是梳理八点法的一些思路。我们引用一段 colmap 中的源码来解读上述过程:
voidDecomposeEssentialMatrix(
const Eigen : : Matrix3d& E, Eigen : : Matrix3d∗ R1,
Eigen : : Matrix3d∗ R2, Eigen : : Vector3d∗ t )
{
// 根据对极约束得到的带噪声的E做SVD分解
Eigen::JacobiSVD svd(
E, Eigen : : ComputeFullU | Eigen : : ComputeFullV ) ;
Eigen::Matrix3d U = svd.matrixU();
Eigen::Matrix3d V = svd.matrixV().transpose();
// 保证行列式符号为正
if (U.determinant() < 0) {
U ∗= −1;
}
if (V.determinant() < 0) {
V ∗= −1;
}
Eigen : : Matrix3d W;
W<< 0, 1, 0, −1, 0, 0, 0, 0, 1;
∗R1 = U ∗ W ∗ V;
∗R2=U∗W.transpose() ∗V;
∗t = U. col (2). normalized ();
}
void PoseFromEssentialMatrix ( const Eigen : : Matrix3d& E,
const std : : vector& points1 ,
const std : : vector& points2 ,
Eigen : : Matrix3d∗ R, Eigen : : Vector3d∗ t ,
std : : vector∗ points3D ) { 7
CHECK_EQ(points1 . size () , points2 . size ());
Eigen::Matrix3d R1;
Eigen::Matrix3d R2;
DecomposeEssentialMatrix(E, &R1, &R2, t );
// Generate all possible projection matrix combinations.
const std : : array R_cmbs{{R1, R2, R1, R2}};
const std : : array t_cmbs{{∗t , ∗t , −∗t , −∗t }};
...
}
这里为什么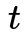 取
取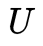 的最后一行可以留给读者作为一个思考题,提示是
的最后一行可以留给读者作为一个思考题,提示是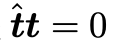 ,然后分析一下矩阵的秩。八点法十分简洁(当然证明过程比较复杂),但是在实际使用过程中,还是会遇到许多问题的,我们在以下简要列举:1. Number of points. 由于 Normalized Essential Matrix 的自由度为 5,在比较 general 的情况下,最少选取的 correspondence 点对为 5(Kruppa在 1913 年的时候给出了五点法,类似八点法会产生 4 个满足对极约束的解,五点法会产生 10个解),因此选取多少点是一个需要实际使用中考虑的问题。2. Number of solutions and positive depth constraint.虽然八点法给出了四对解,但是实际上只有一个正确解,那么其他三个解怎么排除呢?首先从代数层面,不要忘了最原始的表达式
,然后分析一下矩阵的秩。八点法十分简洁(当然证明过程比较复杂),但是在实际使用过程中,还是会遇到许多问题的,我们在以下简要列举:1. Number of points. 由于 Normalized Essential Matrix 的自由度为 5,在比较 general 的情况下,最少选取的 correspondence 点对为 5(Kruppa在 1913 年的时候给出了五点法,类似八点法会产生 4 个满足对极约束的解,五点法会产生 10个解),因此选取多少点是一个需要实际使用中考虑的问题。2. Number of solutions and positive depth constraint.虽然八点法给出了四对解,但是实际上只有一个正确解,那么其他三个解怎么排除呢?首先从代数层面,不要忘了最原始的表达式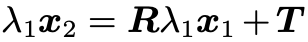 ,在这个表达式中隐藏了一个很关键的约束,深度值应该为正,至于怎么求深度值是三角化部分的知识了,我们不在这里讨论,如果你对上述过程熟悉,不难发现就是一个叉乘的技巧。基于这一约束我们可以将正确的解筛选出来。而从几何层面来看,就是下面这张图(From Multiple View Geometry in Computer Vision):
,在这个表达式中隐藏了一个很关键的约束,深度值应该为正,至于怎么求深度值是三角化部分的知识了,我们不在这里讨论,如果你对上述过程熟悉,不难发现就是一个叉乘的技巧。基于这一约束我们可以将正确的解筛选出来。而从几何层面来看,就是下面这张图(From Multiple View Geometry in Computer Vision): 3. Structure requirement: general position.当观测到的空间点满足某些导致退化的条件时(called critical surfaces),使用八点法会遇到解不唯一的情况。一个典型的例子就是观测点共面的情况,这种时候我们需要使用homography 来解决。4. Motion requirement: sufficient parallax.也就是说,平移量不能为0(为0时也要使用 homography)。需要十分小心的是,在没有平移移动且匹配十分 noise 的时候,八点法依旧会得到一个很奇怪的平移部分的解,而这个解是毫无意义的。5. Multiple motion hypotheses.运动物体场景,这又是另一个问题了。03结语Essential Matrix 之所以叫 Essential Matrix,就是因为它太重要了, 马老师花了4节课的时间,介绍two view geometry的内容, 可见其重要性。目前学术的研究主要在于recognition的问题了,也有许多工作还是聚焦在end to end的执着,当然这只是我个人的一些粗浅的看法。审核编辑 :李倩
3. Structure requirement: general position.当观测到的空间点满足某些导致退化的条件时(called critical surfaces),使用八点法会遇到解不唯一的情况。一个典型的例子就是观测点共面的情况,这种时候我们需要使用homography 来解决。4. Motion requirement: sufficient parallax.也就是说,平移量不能为0(为0时也要使用 homography)。需要十分小心的是,在没有平移移动且匹配十分 noise 的时候,八点法依旧会得到一个很奇怪的平移部分的解,而这个解是毫无意义的。5. Multiple motion hypotheses.运动物体场景,这又是另一个问题了。03结语Essential Matrix 之所以叫 Essential Matrix,就是因为它太重要了, 马老师花了4节课的时间,介绍two view geometry的内容, 可见其重要性。目前学术的研究主要在于recognition的问题了,也有许多工作还是聚焦在end to end的执着,当然这只是我个人的一些粗浅的看法。审核编辑 :李倩
声明:本文内容及配图由入驻作者撰写或者入驻合作网站授权转载。文章观点仅代表作者本人,不代表电子发烧友网立场。文章及其配图仅供工程师学习之用,如有内容侵权或者其他违规问题,请联系本站处理。
举报投诉
-
相机
+关注
关注
4文章
1350浏览量
53577 -
3D视觉
+关注
关注
4文章
431浏览量
27515 -
视图
+关注
关注
0文章
140浏览量
6574
原文标题:双视图几何:你真的理解吗?
文章出处:【微信号:3D视觉工坊,微信公众号:3D视觉工坊】欢迎添加关注!文章转载请注明出处。
发布评论请先 登录
相关推荐
如何通俗理解视觉定位?带你看懂对极几何与基本矩阵
本文为大家介绍对极几何与基本矩阵这两个视觉定位原理。对极几何提到对极几何,一定是对二幅图像而言,对极几何实际上是“两幅图像之间的对极几何”,
发表于 06-01 08:00
你真的懂Word吗
在日常办公当中, Word文档就是我们最常用的软件之一。用它我们写论文、写方案、写小说等等。但是,你真的懂Word吗?其实,Word软件背后,还有一大批隐藏技能你不知道。掌握他们,你将
发表于 01-12 08:22
MCUXpresso查看GPIO值,外围设备视图是空的的原因?
我需要查看 GPIO 值,但外围设备视图是空的。需要做什么来填充外围设备视图?我真的希望不要使用 NXP Semiconductors MCU 应用程序调试器,因为我的调试会话需要支持在闪存中保留一些空间。我正在使用 GDB P
发表于 05-09 10:00
如何才能看懂电子元器件规格书里的三视图
电子元器件规格书里的三视图,或者电子零件规格书里的三视图其实是三视图里面最简单不过的三视图,我们还是要了解一些三视图的基本概念,这样对我们更
发表于 11-09 15:27
•3.5w次阅读
多表物化视图的需求分析及实现应用设计
要了解物化视图可以先了解视图的概念。视图是一个虚拟表(也可以认为是一条语句),基于它创建时指定的查询语句返回的结果集。而物化视图则是将这个虚拟表进行实体化,其本身可以




 双视图几何:你真的理解吗?
双视图几何:你真的理解吗?










评论