前文用 [单调栈解决三道算法问题]介绍了单调栈这种特殊数据结构,本文写一个类似的数据结构「单调队列」。
也许这种数据结构的名字你没听过,其实没啥难的,就是一个「队列」,只是使用了一点巧妙的方法,使得 队列中的元素全都是单调递增(或递减)的 。
「单调栈」主要解决 Next Great Number 一类算法问题,而「单调队列」这个数据结构可以解决滑动窗口问题。我们之前的爆文 [滑动窗口解题套路框架]) 讲的滑动窗口算法是双指针技巧的一种,是解决子串、子数组的通用技巧;而本文说的滑动窗口是比较具体的问题。
比如说力扣第 239 题「滑动窗口最大值」,难度 Hard :
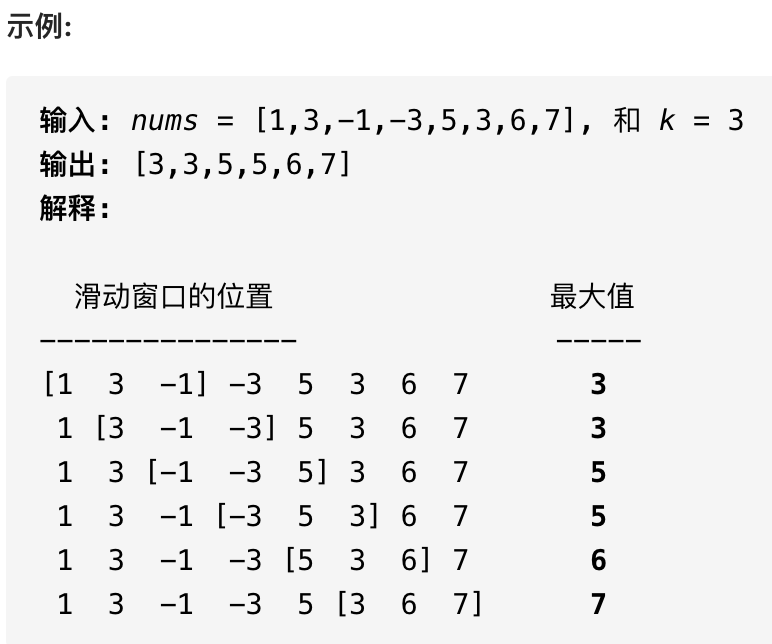
给你输入一个数组nums和一个正整数k,有一个大小为k的窗口在nums上从左至右滑动,请你输出每次窗口中k个元素的最大值。
函数签名如下:
int[] maxSlidingWindow(int[] nums, int k);
比如说题目给出的一个示例:
一、搭建解题框架
这道题不复杂,难点在于如何在O(1)时间算出每个「窗口」中的最大值,使得整个算法在线性时间完成。这种问题的一个特殊点在于,「窗口」是不断滑动的,也就是你得动态地计算窗口中的最大值。
对于这种动态的场景,很容易得到一个结论:
在一堆数字中,已知最值为A,如果给这堆数添加一个数B,那么比较一下A和B就可以立即算出新的最值;但如果减少一个数,就不能直接得到最值了,因为如果减少的这个数恰好是A,就需要遍历所有数重新找新的最值 。
回到这道题的场景,每个窗口前进的时候,要添加一个数同时减少一个数,所以想在 O(1) 的时间得出新的最值,不是那么容易的,需要「单调队列」这种特殊的数据结构来辅助。
一个普通的队列一定有这两个操作:
class Queue {
// enqueue 操作,在队尾加入元素 n
void push(int n);
// dequeue 操作,删除队头元素
void pop();
}
一个「单调队列」的操作也差不多:
class MonotonicQueue {
// 在队尾添加元素 n
void push(int n);
// 返回当前队列中的最大值
int max();
// 队头元素如果是 n,删除它
void pop(int n);
}
当然,这几个 API 的实现方法肯定跟一般的 Queue 不一样,不过我们暂且不管,而且认为这几个操作的时间复杂度都是 O(1),先把这道「滑动窗口」问题的解答框架搭出来:
int[] maxSlidingWindow(int[] nums, int k) {
MonotonicQueue window = new MonotonicQueue();
List
这个思路很简单,能理解吧?下面我们开始重头戏,单调队列的实现。
二、实现单调队列数据结构
观察滑动窗口的过程就能发现,实现「单调队列」必须使用一种数据结构支持在头部和尾部进行插入和删除,很明显双链表是满足这个条件的。
「单调队列」的核心思路和「单调栈」类似,push方法依然在队尾添加元素,但是要把前面比自己小的元素都删掉:
class MonotonicQueue {
// 双链表,支持头部和尾部增删元素
private LinkedList<Integer> q = new LinkedList<>();
public void push(int n) {
// 将前面小于自己的元素都删除
while (!q.isEmpty() && q.getLast() < n) {
q.pollLast();
}
q.addLast(n);
}
}
你可以想象,加入数字的大小代表人的体重,把前面体重不足的都压扁了,直到遇到更大的量级才停住。

如果每个元素被加入时都这样操作,最终单调队列中的元素大小就会保持一个单调递减的顺序,因此我们的max方法可以可以这样写:
public int max() {
// 队头的元素肯定是最大的
return q.getFirst();
}
pop方法在队头删除元素n,也很好写:
public void pop(int n) {
if (n == q.getFirst()) {
q.pollFirst();
}
}
之所以要判断data.front() == n,是因为我们想删除的队头元素n可能已经被「压扁」了,可能已经不存在了,所以这时候就不用删除了:

至此,单调队列设计完毕,看下完整的解题代码:
/* 单调队列的实现 */
class MonotonicQueue {
LinkedList
有一点细节问题不要忽略,在实现MonotonicQueue时,我们使用了 Java 的LinkedList,因为链表结构支持在头部和尾部快速增删元素;而在解法代码中的res则使用的ArrayList结构,因为后续会按照索引取元素,所以数组结构更合适。
三、算法复杂度分析
读者可能疑惑,push操作中含有 while 循环,时间复杂度应该不是O(1)呀,那么本算法的时间复杂度应该不是线性时间吧?
单独看push操作的复杂度确实不是O(1),但是算法整体的复杂度依然是O(N)线性时间。要这样想,nums中的每个元素最多被push_back和pop_back一次,没有任何多余操作,所以整体的复杂度还是O(N)。
空间复杂度就很简单了,就是窗口的大小O(k)。
其实我觉得,这种特殊数据结构的设计还是蛮有意思的,你学会单调队列的使用了吗?学会了给个三连?
-
数据结构
+关注
关注
3文章
573浏览量
40254 -
队列
+关注
关注
1文章
46浏览量
10932
发布评论请先 登录
相关推荐
什么是数据结构(Data Structrue)
基于参数化存储结构的滑动窗口IP核自动生成
GPIB命令的数据结构
什么是数据结构
数据结构是什么_数据结构有什么用
为什么要学习数据结构?数据结构的应用详细资料概述免费下载
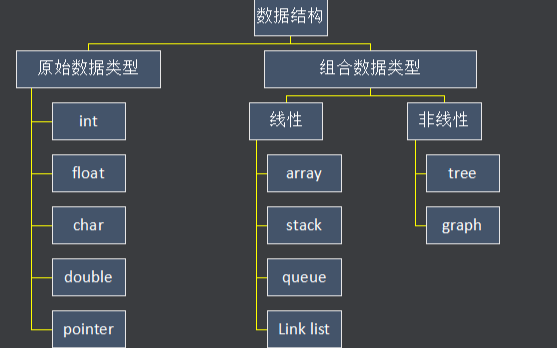
什么是数据结构?为什么要学习数据结构?数据结构的应用实例分析
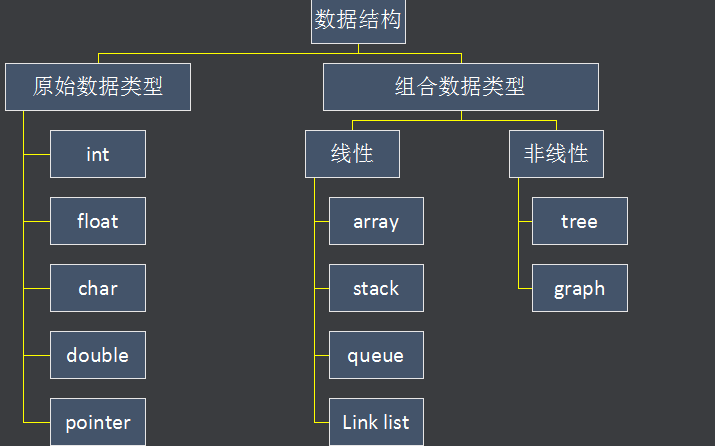
NetApp的数据结构是如何演变的

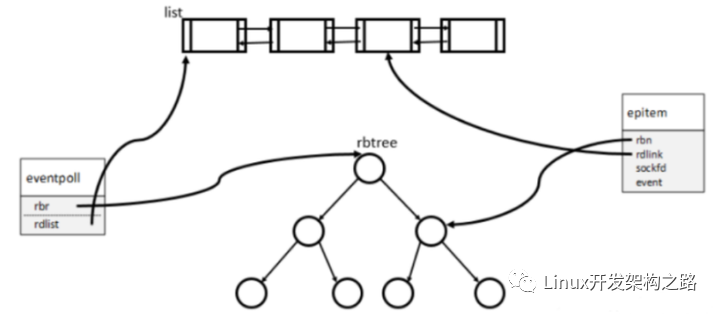
epoll的基础数据结构




 数据结构解决滑动窗口问题
数据结构解决滑动窗口问题











评论