经常拿回溯算法来说事儿的,无非就是八皇后问题和数独问题了。那我们今天就通过实际且有趣的例子来讲一下如何用回溯算法来解决数独问题。
一、直观感受
说实话我小的时候也尝试过玩数独游戏,但从来都没有完成过一次。做数独是有技巧的,我记得一些比较专业的数独游戏软件,他们会教你玩数独的技巧,不过在我看来这些技巧都太复杂,我根本就没有兴趣看下去。
不过自从我学习了算法,多困难的数独问题都拦不住我了。下面是我用程序完成数独的一个例子:

PS:GIF 可能出现 bug,若卡住点开查看即可,下同。
这是一个安卓手机中的数独游戏,我使用一个叫做 Auto.js 的脚本引擎,配合回溯算法来实现自动完成填写,并且算法记录了执行次数。
在后文,我会给出该脚本的实现思路代码以及软件工具的下载,你也可以拿来装逼用 。
可以观察到前两次都执行了 1 万多次,而最后一次只执行了 100 多次就算出了答案,这说明对于不同的局面,回溯算法得到答案的时间是不相同的。
那么计算机如何解决数独问题呢?其实非常的简单,就是穷举嘛,下面我可视化了求解过程:

算法的核心思路非常非常的简单,就是对每一个空着的格子穷举 1 到 9,如果遇到不合法的数字(在同一行或同一列或同一个 3×3 的区域中存在相同的数字)则跳过,如果找到一个合法的数字,则继续穷举下一个空格子 。
对于数独游戏,也许我们还会有另一个误区:就是下意识地认为如果给定的数字越少那么这个局面的难度就越大。
这个结论对人来说应该没毛病,但对于计算机而言,给的数字越少,反而穷举的步数就越少,得到答案的速度越快,至于为什么,我们后面探讨代码实现的时候会讲。
上一个 GIF 是最后一关 70 关,下图是第 52 关,数字比较多,看起来似乎不难,但是我们看一下算法执行的过程:

可以看到算法在前两行穷举了半天都没有走出去,由于时间原因我就没有继续录制了,事实上,这个局面穷举的次数大概是上一个局面的 10 倍。
言归正传,下面我们就来具体探讨一下如何用算法来求解数独问题,顺便说说我是如何可视化这个求解过程的 。
二、代码实现
首先,我们不用管游戏的 UI,先单纯地解决回溯算法,LeetCode 第 37 题就是解数独的问题,算法函数签名如下:
void solveSudoku(char[][] board);
输入是一个9x9的棋盘,空白格子用点号字符.表示,算法需要在原地修改棋盘,将空白格子填上数字,得到一个可行解。
至于数独的要求,大家想必都很熟悉了,每行,每列以及每一个 3×3 的小方格都不能有相同的数字出现。那么,现在我们直接套回溯框架即可求解。
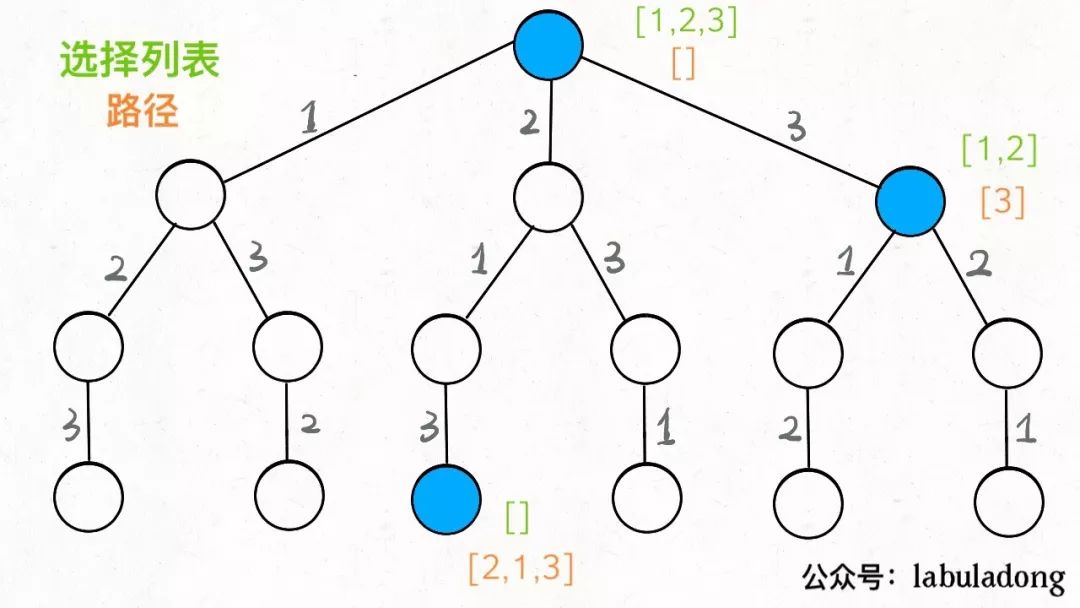
前文 [回溯算法详解],已经写过了回溯算法的套路框架,如果还没看过那篇文章的,建议先看看 。
回忆刚才的 GIF 图片,我们求解数独的思路很简单粗暴,就是对每一个格子所有可能的数字进行穷举。对于每个位置,应该如何穷举,有几个选择呢?
很简单啊,从 1 到 9 就是选择,全部试一遍不就行了 :
// 对 board[i][j] 进行穷举尝试
void backtrack(char[][] board, int i, int j) {
int m = 9, n = 9;
for (char ch = '1'; ch <= '9'; ch++) {
// 做选择
board[i][j] = ch;
// 继续穷举下一个
backtrack(board, i, j + 1);
// 撤销选择
board[i][j] = '.';
}
}
emmm,再继续细化,并不是 1 到 9 都可以取到的,有的数字不是不满足数独的合法条件吗?而且现在只是给j加一,那如果j加到最后一列了,怎么办?
很简单,当j到达超过每一行的最后一个索引时,转为增加i开始穷举下一行,并且在穷举之前添加一个判断,跳过不满足条件的数字 :
void backtrack(char[][] board, int i, int j) {
int m = 9, n = 9;
if (j == n) {
// 穷举到最后一列的话就换到下一行重新开始。
backtrack(board, i + 1, 0);
return;
}
// 如果该位置是预设的数字,不用我们操心
if (board[i][j] != '.') {
backtrack(board, i, j + 1);
return;
}
for (char ch = '1'; ch <= '9'; ch++) {
// 如果遇到不合法的数字,就跳过
if (!isValid(board, i, j, ch))
continue;
board[i][j] = ch;
backtrack(board, i, j + 1);
board[i][j] = '.';
}
}
// 判断 board[r][c] 是否可以填入 n
boolean isValid(char[][] board, int r, int c, char n) {
for (int i = 0; i < 9; i++) {
// 判断行是否存在重复
if (board[r][i] == n) return false;
// 判断列是否存在重复
if (board[i][c] == n) return false;
// 判断 3 x 3 方框是否存在重复
if (board[(r/3)*3 + i/3][(c/3)*3 + i%3] == n)
return false;
}
return true;
}
emmm,现在基本上差不多了,还剩最后一个问题:这个算法没有 base case,永远不会停止递归。这个好办,什么时候结束递归? 显然r == m的时候就说明穷举完了最后一行,完成了所有的穷举,就是 base case 。
另外,前文也提到过,为了减少复杂度,我们可以让backtrack函数返回值为boolean,如果找到一个可行解就返回 true,这样就可以阻止后续的递归。只找一个可行解,也是题目的本意。
最终代码修改如下:
boolean backtrack(char[][] board, int i, int j) {
int m = 9, n = 9;
if (j == n) {
// 穷举到最后一列的话就换到下一行重新开始。
return backtrack(board, i + 1, 0);
}
if (i == m) {
// 找到一个可行解,触发 base case
return true;
}
if (board[i][j] != '.') {
// 如果有预设数字,不用我们穷举
return backtrack(board, i, j + 1);
}
for (char ch = '1'; ch <= '9'; ch++) {
// 如果遇到不合法的数字,就跳过
if (!isValid(board, i, j, ch))
continue;
board[i][j] = ch;
// 如果找到一个可行解,立即结束
if (backtrack(board, i, j + 1)) {
return true;
}
board[i][j] = '.';
}
// 穷举完 1~9,依然没有找到可行解,此路不通
return false;
}
boolean isValid(char[][] board, int r, int c, char n) {
// 见上文
}
现在可以回答一下之前的问题,为什么有时候算法执行的次数多,有时候少?为什么对于计算机而言,确定的数字越少,反而算出答案的速度越快 ?
我们已经实现了一遍算法,掌握了其原理,回溯就是从 1 开始对每个格子穷举,最后只要试出一个可行解,就会立即停止后续的递归穷举。所以暴力试出答案的次数和随机生成的棋盘关系很大,这个是说不准的。
那么你可能问, 既然运行次数说不准,那么这个算法的时间复杂度是多少呢 ?
对于这种时间复杂度的计算,我们只能给出一个最坏情况,也就是 O(9^M),其中M是棋盘中空着的格子数量。你想嘛,对每个空格子穷举 9 个数,结果就是指数级的。
这个复杂度非常高,但稍作思考就能发现,实际上我们并没有真的对每个空格都穷举 9 次,有的数字会跳过,有的数字根本就没有穷举,因为当我们找到一个可行解的时候就立即结束了,后续的递归都没有展开。
这个 O(9^M) 的复杂度实际上是完全穷举,或者说是找到所有可行解的时间复杂度。
如果给定的数字越少,相当于给出的约束条件越少,对于计算机这种穷举策略来说,是更容易进行下去,而不容易走回头路进行回溯的,所以说 如果仅仅找出一个可行解 ,这种情况下穷举的速度反而比较快。
至此,回溯算法就完成了,你可以用以上代码通过 LeetCode 的判题系统,下面我们来简单说下我是如何把这个回溯过程可视化出来的。
三、算法可视化
让算法帮我玩游戏的核心是算法,如果你理解了这个算法,剩下就是借助安卓脚本引擎 Auto.js 调 API 操作手机了,工具我都放在后台了,你等会儿就可以下载。
用伪码简单说下思路,我可以写两个函数:
void setNum(Button b, char n) {
// 输入一个方格,将该方格设置为数字 n
}
void cancelNum(Button b) {
// 输入一个方格,将该方格上的数字撤销
}
回溯算法的核心框架如下, 只要在框架对应的位置加上对应的操作,即可将算法做选择、撤销选择的过程完全展示出来 ,也许这就是套路框架的魅力所在:
for (char ch = '1'; ch <= '9'; ch++) {
Button b = new Button(r, c);
// 做选择
setNum(b, ch);
board[i][j] = ch;
// 继续穷举下一个
backtrack(board, i, j + 1);
// 撤销选择
cancelNum(b);
board[i][j] = '.';
}
-
回溯算法
+关注
关注
0文章
10浏览量
6591 -
数独游戏开发
+关注
关注
0文章
2浏览量
5236
发布评论请先 登录
相关推荐
回溯经典 (五皇后问题) (算法)
基于回溯的RFID防冲撞算法
模板方法模式在回溯算法中的应用
模板方法模式在回溯算法中的应用
Viterbi译码器回溯算法实现

基于Arduino的电子数独游戏的制作教程





 搞懂回溯算法,做数独都变简单了
搞懂回溯算法,做数独都变简单了











评论