因为六步换向法存在一些缺点,FOC算法有控制起来转矩波动小,动态响应快的特点,能让电机转动更加平滑并且高效。
FOC算法是什么原理呢?
简单来说,其实就是FOC控制算法可以实现对电压的矢量控制,间接地控制电流。这种算法其实可以看做是正弦波控制的升级版,即通过实现电流矢量的控制,让电机定子磁场也实现矢量控制效果。进而控制电机定子磁场方向,让电机定子磁场方向与转子磁场方向保持一直角,从而让电机实现最大扭矩输出。
那么FOC算法是怎么实现的呢?
归纳一下,其实就是对电机定子转子的磁场来建立数学坐标系,并经过一系列坐标变换,再基于目标位置、转速、扭矩等计算输出目标控制占空比(SVPWM)。
为什么要变换坐标系呢,因为对于三相直流电机的数学模型,三相坐标系计算起来很复杂,但其实坐标轴是相对静止的,所以我们可以将三相坐标系变换为两相坐标系,以此来简化计算方法。
0
7
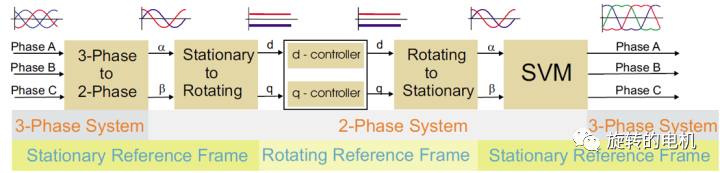
FOC算法控制架构 (核心)
大致画了一个FOC控制架构的架构图,大家可以很清晰的看到架构中包含有哪些模块。
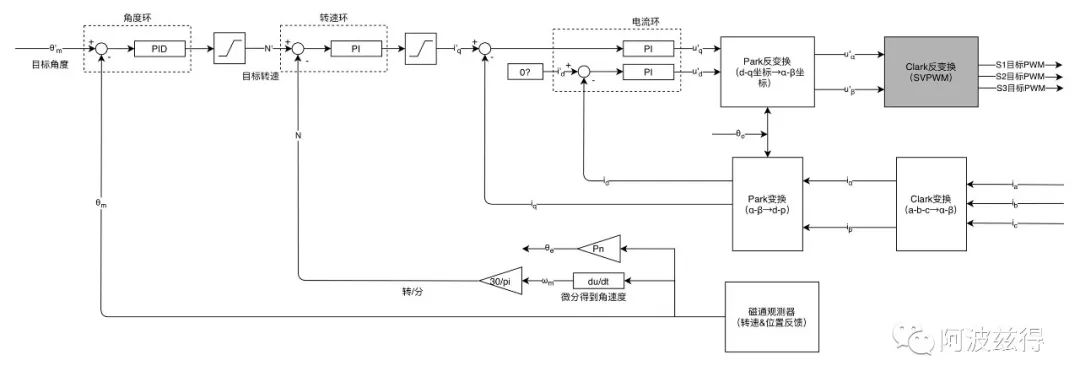
基本上分为Clark变换、Park变换、Park反变换、SVPWM,以及角度环、转速环、电流环等几部分。
首先我们需要了解的是在电机定子、转子磁场中,是如何建立数学坐标系的,明白坐标系建立的含义后,这Clark/Park的变换和反变换也就明白了。
0
8
电机磁场的数学模型建立 (核心)
总体示****意图:
首先我们可以看到这是一个电机横切剖面的俯视图,带有NS极的标记为转子,转子以ω为转速逆时针转动;棕色的圈标记为定子,在定子周围有A、B、C三相通电绕组线圈。
我们可以在图中看到三个坐标系,分别是A-B-C轴坐标系、α-β轴坐标系、d-q轴坐标系。
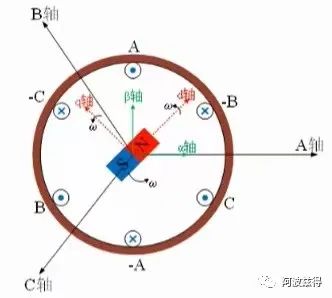
ABC轴坐标系建立:
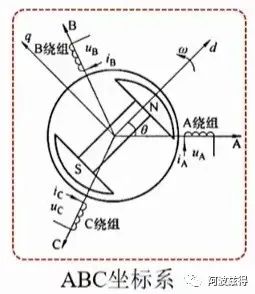
| 坐标轴 | A轴、B轴、C轴 |
|---|---|
| 坐标轴含义 | 以A、B、C三相绕组线圈通电后,产生的磁感应强度N极方向分别为A、B、C轴的方向。 |
| 坐标轴性质 | 静止坐标系 |
| 备注 | 空间上任一矢量在三个坐标系上的投影代表了该矢量在三个绕组上的分量。 |
α-β轴坐标系建立:
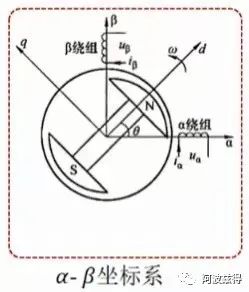
| 坐标轴 | α轴、β轴 |
|---|---|
| 坐标轴含义 | α轴与三相定子坐标系A轴重合,β轴逆时针超前α轴90度电角度 |
| 坐标轴性质 | 静止坐标系 |
| 备注 | 两相绕组也能旋转磁场,故可以将三相绕组与两相绕组可以等效,数学上用两相直角坐标系描述比较简便,所以可以将A-B-C三相坐标轴等效为α-β两相坐标轴。 |
d-q轴坐标系建立:
| 坐标轴 | d轴、q轴 |
|---|---|
| 坐标轴含义 | d轴位于转子磁极轴线上,与N极方向相同,q 轴逆时针超前d 轴90 度空间电角度,该坐标系和转子一起在空间上以转子角速度旋转 |
| 坐标轴性质 | 旋转坐标系 |
| 备注 | 以角速度ω(与转子同一角速度)旋转,那么在d-q轴绕组中通以直流电流,将产生一个旋转磁动势,与静止的α-β轴中角频率为ω的交流电流产生的旋转磁动势相同 |
下次详细介绍FOC算法模块中,Clark变换/反变换及Park变换/反变换的数学模型公式计算。
-
控制算法
+关注
关注
4文章
167浏览量
21848 -
FOC
+关注
关注
20文章
326浏览量
43105 -
转子磁场
+关注
关注
0文章
2浏览量
5296 -
控制电机
+关注
关注
0文章
242浏览量
18318
发布评论请先 登录
相关推荐
永磁同步电机控制系统仿真—FOC控制算法的Simulink模型
FOC控制算法的Simulink模型
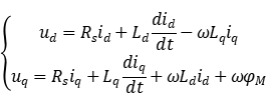




 磁场矢量定向控制算法(FOC)简介
磁场矢量定向控制算法(FOC)简介











评论