电阻和运算放大器中的温度漂移——闪烁噪声和信号平均

了解电子电路（即电阻器和放大器）中的温度漂移。 我们还将介绍闪烁噪声的影响如何发挥作用，以及漂移如何限制信号平均的有效性。

即使在固定的电气条件（电源电压、输入和负载）下，电子电路也不会完全稳定，因为它们往往会随时间和温度漂移。 这些与理想行为的偏差会给精密测量增加相当大的误差。 为了深入了解电子产品的温度漂移，本文简要介绍了电阻和放大器的温度行为。 我们还将讨论闪烁噪声的影响可能不容易与输出中温度引起的漂移区分开来。 最后，我们将讨论漂移会限制
信号平均技术 通常用于提高可重复测量的准确性。

电阻温度漂移—电阻温度系数

作为最简单的电子元件类型，电阻器作为高性能电路中的误差源可能会被忽视。 但是，电阻器的值不是恒定的，并且随温度和时间而变化。 例如，如果电阻的温度系数为±50
ppm/°C，环境温度比参考温度（室温）高100°C，则电阻的值可以变化±0.5%。

幸运的是，在许多应用中，电路精度由两个或多个电阻的比值决定，而不是单个电阻的绝对值。 在这些情况下，匹配的电阻网络，例如
LT5400，可以使用。 电阻形成一个共基板网络，并表现出良好匹配的温度行为。 图1比较了单个分立电阻与匹配电阻网络的温度行为。

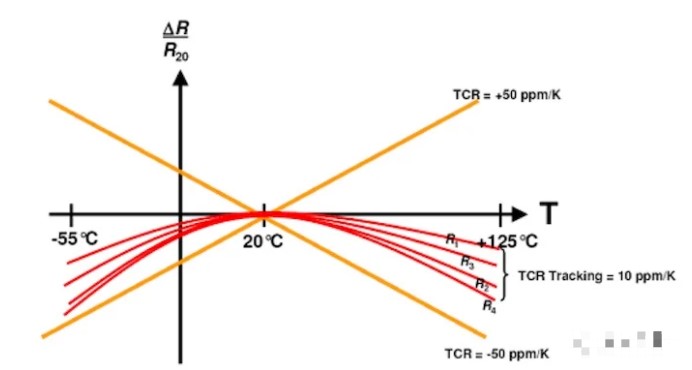
*图1. 匹配电阻网络温度行为的分立电阻。 图片由 维沙伊

在此图中，橙色线表示单个±50 ppm/°C电阻值的变化限值，因为温度从参考温度（20°C）沿任一方向变化。 红色曲线对应于来自匹配电阻网络的四个电阻，它们表现出相似的温度行为。 匹配电阻的温度系数 （TC） 相互跟踪，通常在 2–10 ppm/°C 以内。 具有良好匹配温度行为的电阻器可能是某些精密应用的基本要求，例如 电阻电流检测.

具有相同温度系数的温度感应漂移

应该注意的是，即使TC值相同，电路中的电阻也会产生与温度相关的漂移。 下面可以看到图 2 中的示例。

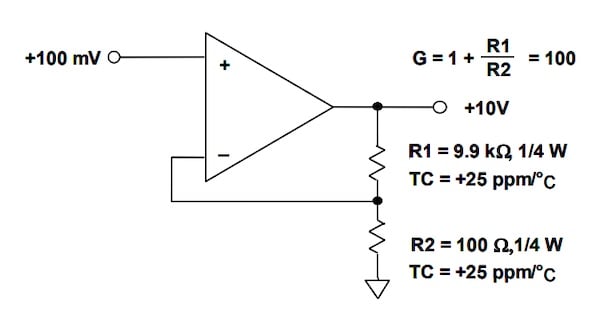
*图2. 产生温度相关漂移的示例。 **图片 [修改] 使用由 ADI公司]

在上图中，两个电阻具有相同的TC（+25 ppm/°C）; 然而，电阻两端的电压以及两个电阻的功耗非常不同。 R两端的电压2 = 100 Ω为0.1 V，功耗为0.1 mW。 然而，电压两端的电压R.1 为 9.9 V; 因此，该电阻两端的功耗为9.9 mW。 假设 热阻两个电阻均为125°C/W，温度为R1 和 R2 将分别比环境温度升高1.24°C和0.0125°C。 这种不相等的自热效应导致两个电阻漂移不同的量。

图3（a）显示了另一个示例，其中相同的TC不一定能解决温度漂移问题。

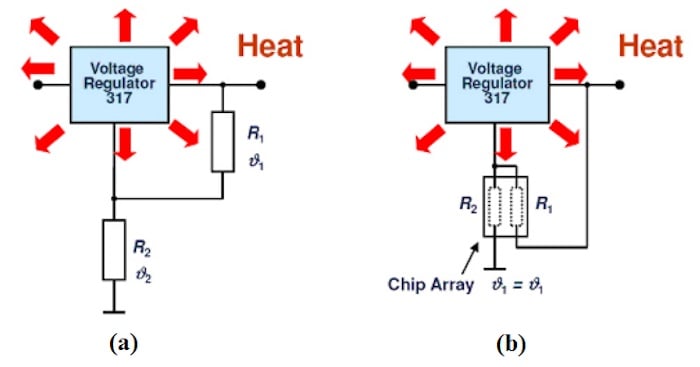
图3. 使用（a）分立电阻器表示不同本地环境温度的示例，以及（b）使用集成电阻器/电阻器阵列表示相同的局部环境温度的示例。 *图片由 维沙伊

在上图中，如果设计包含不相等电阻（R1 ≠· 2 ），在相同的TC下，电阻的自发热会产生温度引起的漂移，如上所述。 但是，稳压器可能会引起额外的温度梯度。 即使两个电阻的电阻和TC相同（R1 = R2 和 TC1 = TC 2 ).

可以使用电阻阵列来避免上述示例的漂移问题（图 3（b））。 在单个基板上实现电阻网络时，两个电阻器热耦合并经历相同的环境温度。

其他电路中的温度漂移—运算放大器温度漂移

由于简单的电阻容易受到温度和老化的影响，因此其他更复杂的电路的参数也随温度和时间漂移也就不足为奇了。 例如，放大器的输入失调电压随温度和时间而变化。 这会产生时变误差，限制可测量的最小直流信号。 典型通用精密运算放大器的失调漂移范围为1–10
μV/°C。

如果放大器的失调漂移限制了测量精度，我们可以考虑使用斩波稳定放大器。 这些器件使用失调消除技术将失调电压降低到非常低的水平（例如，小于10
μV），并产生接近零漂移的操作。 斩波稳定放大器的失调漂移，例如 来自微芯片的MCP6V51，可低至 36 nV/°C。

温度漂移或闪烁噪声（1/f）？

在非常低的频率下，闪烁噪声是影响电路输出的主要噪声源。 闪烁噪声的平均功率与工作频率成反比（这就是为什么闪烁噪声也称为1/f噪声）。 频率越低，1/f噪声的平均功率越高。 如果我们测量电路的输出足够长的时间，我们可以捕获这种低频噪声的影响。 图4显示了闪烁噪声在输出端产生的放动
ADA4622-2.

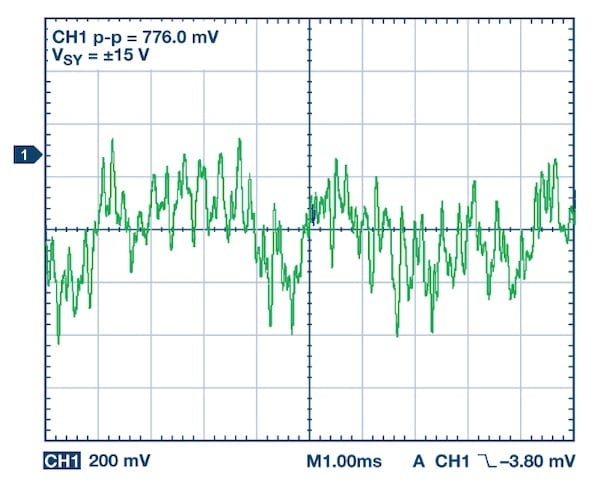
*图4. ADA4622-2输出闪烁噪声的放动。图片由 ADI公司

ADA4622-2是一款精密运算放大器，0.1 Hz至10 Hz噪声典型值为0.75 μV p-p。 上图的波形显示了ADA4622-2的0.1 Hz至10 Hz噪声放大后为1000倍。 如您所见，闪烁噪声会导致输出随机缓慢波动。 这些波动是由不同于温度或老化引起的漂移的现象产生的。 然而，由于其低频特性，1/f噪声的影响可能不容易与信号漂移区分开来。

对于运算放大器，失调漂移和1/f噪声都会在输出端引起缓慢误差。 这就是为什么使用失调消除技术来降低失调漂移的零漂移运算放大器在输出端没有1/f噪声的原因。 图5比较了连续时间放大器与零漂移放大器的1/f噪声。

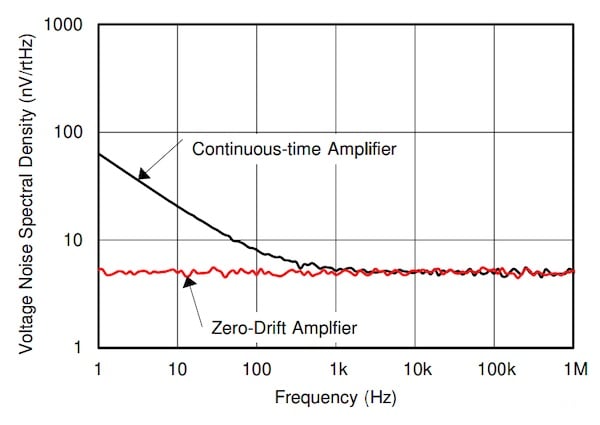
*图5. 连续时间放大器与零漂移放大器的噪声。 图片由 钛

漂移会限制信号平均的有效性吗？

另一种有效的降噪技术是信号平均。 如果我们有一个噪声方差为 σ_n^2的可重复实验，我们可以重复实验 M 次并平均相应的输出样本，以将噪声方差减小为：s2nσn2，我们可以重复实验M次，并对相应的输出样本求平均值，将噪声方差降低到：

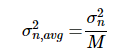
等式 1.

其中 $$
σ_{n， avg}^2

表示平均信号的噪声方差。尽管信号平均在某些应用中有效，但它仍然有其局限性。信号平均基于噪声样本彼此不相关的假设。测量数据中的缓慢漂移可能充当低频相关噪声分量，并限制信号平均技术的有效性。在这种情况下，噪声抑制将低于公式1预测的噪声抑制。s2n,一个在gsn,一个在g2 表示平均信号的噪声方差。尽管信号平均在某些应用中有效，但它仍然有其局限性。信号平均基于噪声样本彼此不相关的假设。测量数据中的缓慢漂移可能充当低频相关噪声分量，并限制信号平均技术的有效性。在这种情况下，噪声抑制将低于公式1预测的噪声抑制。 此外，根据给定应用中随机漂移的类型，平均信号的方差可能会增加到超过某些M值以上。在另一篇文章中，我们将更仔细地研究信号平均技术的这种局限性，并介绍一个有用的统计分析工具，称为 艾伦方差，这使我们能够更深入地了解电路的输出如何由于闪烁噪声、温度效应等不同现象而趋向漂移。