了解低频电荷放大器的限制、时间常数的影响,以及漂移现象如何也会在低频测量中引入误差。
在上一篇文章中,我们讨论了 电荷放大器的时间常数
测量静态信号时会限制精度。 在本文中,我们将继续讨论并更仔细地研究在低频下使用电荷放大器的局限性。 在此过程中,我们将看到,除了时间常数之外,漂移现象还会在我们的低频测量中引入误差。
具有可调时间常数的电荷放大器
如图1所示,一些电荷放大器的反馈路径包含一个可切换电阻和一个复位/测量开关。 这种配置可以根据输入信号的低频成分调整放大器的时间常数。
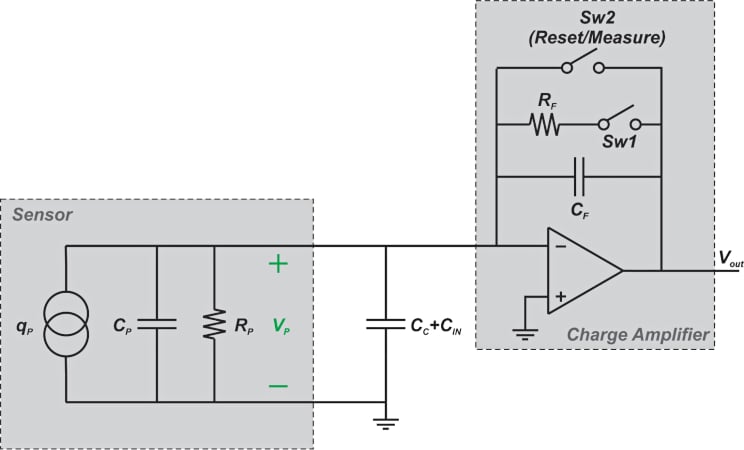
***图1. **使用可切换电阻和复位/测量开关的电荷放大器反馈路径示例。 *
当反馈电阻就位(即SW1闭合和SW2开路)时,在测量直流(或极低频)信号时,有限时间常数可能是误差源。 例如,考虑将图2a所示的梯形加速度信号应用于传感器。 在这种情况下,由于系统的时间常数较短,输出波形的平坦部分会随着时间的推移而衰减(图2b)。
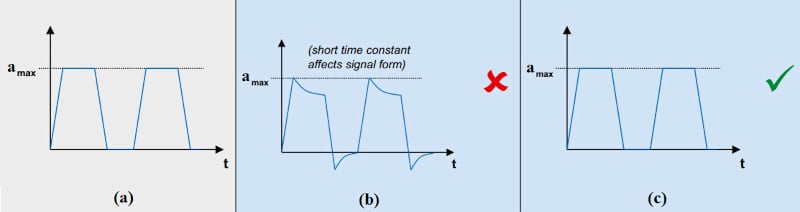
*图2. 梯形加速度信号的例子(a),输出波形的短时间常数衰减程度(b),以及梯形信号的精确测量(c)。 图片(改编)由 奇石乐
为了解决这个问题,应相对于输入脉冲宽度增加时间常数以限制误差。 下图可以表明,对于2%的最大误差,输入信号的平坦区域不应超过放大器时间常数的2%。
T=RFCFτ=RFCF
例如,如果输入信号保持恒定 100 秒,则时间常数应至少为 5000 秒,以将误差保持在 2% 以下。
事实上,RC电路的放电曲线可以被认为是相对线性的,最高可达电路时间常数的10%左右。 基于这一点,我们可以确定处理静态信号时给定持续时间内的误差百分比。 例如,我们可以得出结论,传感器在 $$
\\tau 的 1% 的持续时间内放电 1%。 Tτ.
因此,为了在准静态测量中获得1%的精度,我们必须在传感器时间常数的1%的时间窗口内读取输出读数。 类似的陈述最多可以做$\\tau的10%左右。 Tτ.
使用复位/测量工作模式(SW1 开路,SW2 打开或关闭,具体取决于处于复位或测量操作阶段),我们可以最大化时间常数并更准确地测量梯形信号(图 2c)。 但是,这会使电路更容易发生漂移。
漂移是指电荷放大器输出在一段时间内发生的变化,而不是由被测物理参数的变化引起的(我们讨论中的加速度)。 有几种不同的机制会导致漂移,我们将在以下部分中对此进行研究。
漂移原因一——运算放大器输入偏置电流
漂移的来源之一是运算放大器的输入偏置电流。 图 3 说明了运算放大器输入偏置电流的影响。
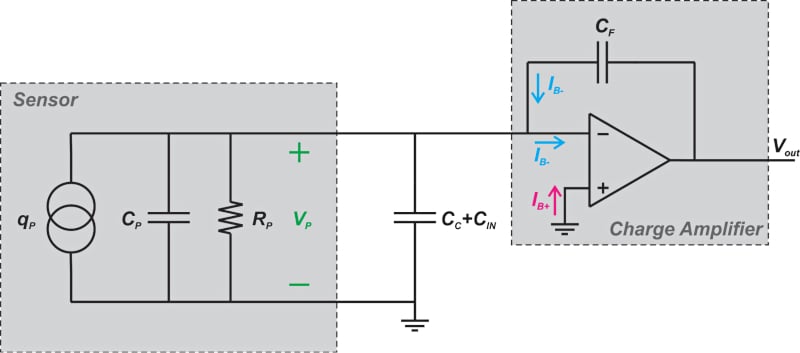
* 图 3. 显示运算放大器输入偏置电流的传感器和电荷放大器图。 *
在上图中,IB- 和我B+ 表示流入运算放大器输入端子的电流。 请注意,该图显示了复位/测量操作模式(RF 被删除)。 由于反相输入位于虚拟地,因此IB-
只能流过反馈 电容器。 这逐渐收费CF 并使输出随时间漂移。 假设我B-=10 fA 和 CF=1 nF。 另外,假设 CF 最初出院。
使用这些值,100秒后的输出电压可以得出为:
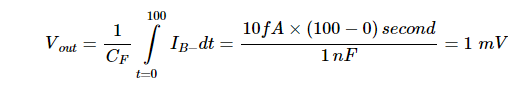
如您所见,100 秒后,输出漂移 1 mV。 这可能会导致问题,特别是当测量与误差相当的小信号时。 请注意,使用反馈电阻的电荷放大器对漂移现象更可靠。 C的阻抗F 理想情况下在 DC 是无限的。 与 RF 就位时,直流反馈路径的主要成分是电阻。 由于反馈路径是阻性而不是容性,因此电路不能充当积分器。 在这种情况下,我B- 只能引起输出和反相输入之间的直流偏移,但理想情况下不能引起漂移。
漂移原因二—运算放大器输入失调电压
另一种可能导致漂移的机制是 输入失调电压 的运算放大器。 如图 4 所示。
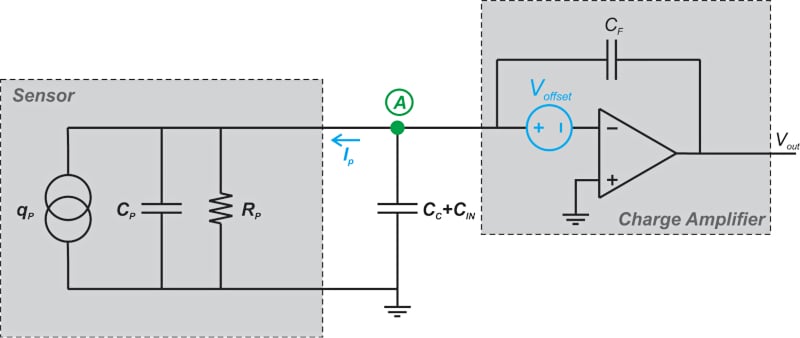
***图4. ****传感器和电荷放大器示意图,显示运算放大器输入失调电压。 *
假设运算放大器具有高增益,可以证明节点A的电位近似等于V 抵消 .
因此,流过传感器绝缘电阻的电流可以发现为:
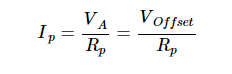
该电流通过反馈电容C提供F 并且会导致漂移,就像运算放大器的输入偏置电流一样。 例如,假设:
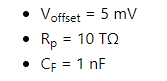
假设 CF 初次放电后,100秒后的输出电压可发现为:
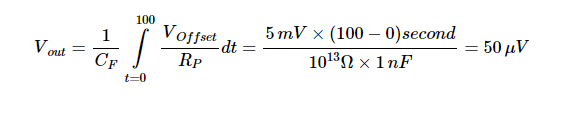
这在许多应用程序中应该可以忽略不计; 但是,应该注意的是,传感器绝缘电阻在较高温度下会显着降低。 例如,在400°C时,传感器绝缘可降至10 MΩ。 在这种情况下,5 mV失调可在20秒内导致10 V漂移,并使放大器完全饱和。 再次,使用 RF 就位时,失调电压产生的直流电流不能充电CF 并且漂移问题得到了理想的解决。
漂移原因三——介电记忆效应
介电记忆效应,或 介电吸收,是一种非理想效应,会在电容器两端产生误差电压。 如图5所示,假设我们将电容器充电至某个电压,然后在短时间内(从t1到t2)放电。
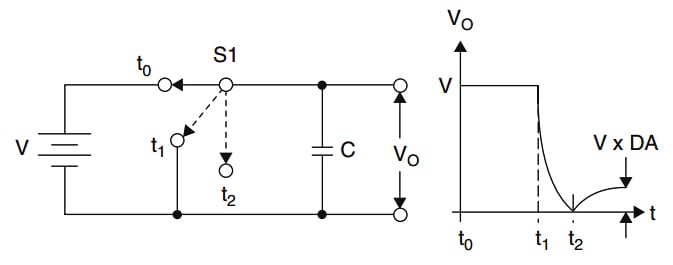
*图5. 放电/充电电容介质吸收后的残余开路电压。 图片由 ADI公司的线性电路设计手册
接下来,我们断开电容器的连接。 理想情况下,我们期望电容器的开路电压保持在零伏。 然而,电容两端的残余电压会慢慢积聚。 例如,如果电容器的初始电压为2.5 V,则典型电容器的误差电压约为120 mV。
当我们对电容器快速放电时,介电记忆效应更为明显。 误差电压与电容器的初始电压以及电容器电介质的特性成正比。 这种效应会导致敏感电路的功能出现问题,例如采样保持电路、积分器和电压-频率转换器。 在电荷放大器中,反馈电容中的介电记忆效应会产生漂移。
除了上面讨论的影响之外,还有其他漂移机制会在电荷放大器中引入误差。
如果漂移电流不是纯直流怎么办?
我们在上面讨论过放置 RF 与反馈电容并联可以理想地解决漂移问题,因为它为漂移机制产生的直流电流创建了替代路径,并且不允许漂移电流为反馈电容充电。 现在要问的问题是,如果漂移电流不是纯直流值并且有一些波动怎么办?
例如,FET(场效应晶体管)运算放大器的输入偏置电流通常随着温度每升高10°C而翻倍。 因此,如果我们的信号调理电子设备遇到较大的温度变化,漂移感应电流可能不被视为纯直流值。 在这种情况下,我们需要选择一个相对较小的RF 以保持反馈路径在漂移电流频率下仍具有阻性。 但是,这种补救措施是以更大的时间常数误差为代价实现的。
图6可以帮助您更好地可视化温度变化对电荷放大器性能的影响。
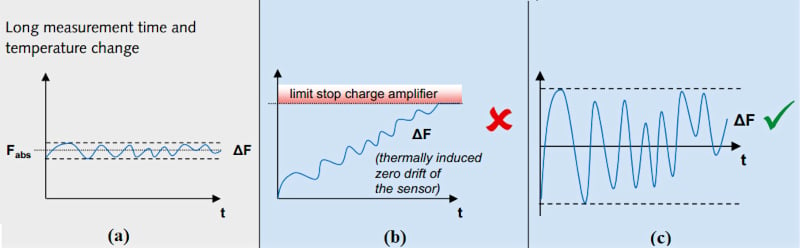
***图6. **温度变化对电荷放大器性能影响的可视化示例。 图片由 奇石乐]
图6a显示了作用在压电传感元件上的力,而图6b显示了电荷放大器的响应,该电荷放大器具有非常大的时间常数并且容易受到漂移的影响。 尽管放大器试图产生与施加的力成比例的输出信号,但由于热引起的漂移,它最终会饱和。 但是,具有较短时间常数的放大器可以成功放大输入信号。
-
放大器
+关注
关注
144文章
13750浏览量
214826 -
漂移
+关注
关注
0文章
12浏览量
14842 -
时间常数
+关注
关注
0文章
24浏览量
13727
发布评论请先 登录
相关推荐
解释标准的连续时间和零漂移放大器之间的差异
标准的连续时间和零漂移放大器之间的差异解释
解读连续时间和零漂移放大器之间的差异
具有负时间常数的DPGA条件信号
电路时间常数怎么求




 了解电荷放大器误差——时间常数和漂移
了解电荷放大器误差——时间常数和漂移










评论