详解数据结构中栈的定义和操作

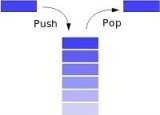
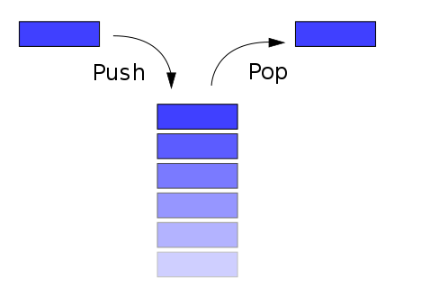
1.栈的定义

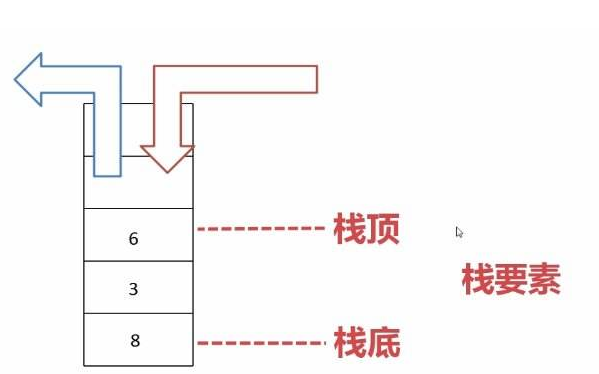
栈（stack）：是只允许在一端进行插入或者删除操作的线性表（即后进先出，大概可以理解为吃饱了吐出来）

空栈：不含元素的空标配

栈顶：表尾端

栈底：表头端

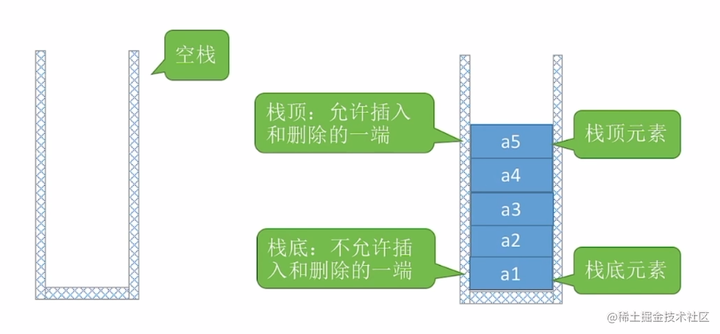
进栈顺序：a1->a2->a3->a4->a5

出栈顺序：a5->a4-a3->a2->a1

2. 对比线性表和栈基本操作

2.1 线性表的基本操作

InitList (&L): 初始化表。构造一个空的线性表 L，分配内存空间

DestoryList (&L): 销毁操作。销毁线性表，并且释放线性表 L 所占用的空间

ListInsert (&L,i,e): 插入操作，在表 L 中的第 i 个位置上插入指定元素 e

ListDelete (&L,i,e): 删除操作，删除表 L 中的第 i 个位置的元素，并且用 e 返回删除元素的值

LocateElem (L,e): 按值查找操作，在表 L 中查找具有给定关键字值的元素

GetElem (L,i): 按位查找操作，获取表 L 中第 i 个位置的元素的值

2.2 栈的基本操作

InitStack (&S): 初始化栈，构造一个空栈 S，分配内存空间

DestoryStack (&S): 销毁栈，销毁并释放栈 S 所占用的内存空间

Push (&S,x): 进栈，若栈 S 未满，则将 x 加入使之成为新的栈顶

Pop (&S,&x): 出栈，若栈 S 非空，则弹出栈顶元素，并用 x 返回

GetTop (S,&x): 读栈顶元素，若栈 S 非空，则用 x 返回栈顶元素

其他常见操作：StackEmpty (S): 判断一个栈 S 是否为空，若 S 为空，则返回 true，否则返回 false

3. 顺序栈

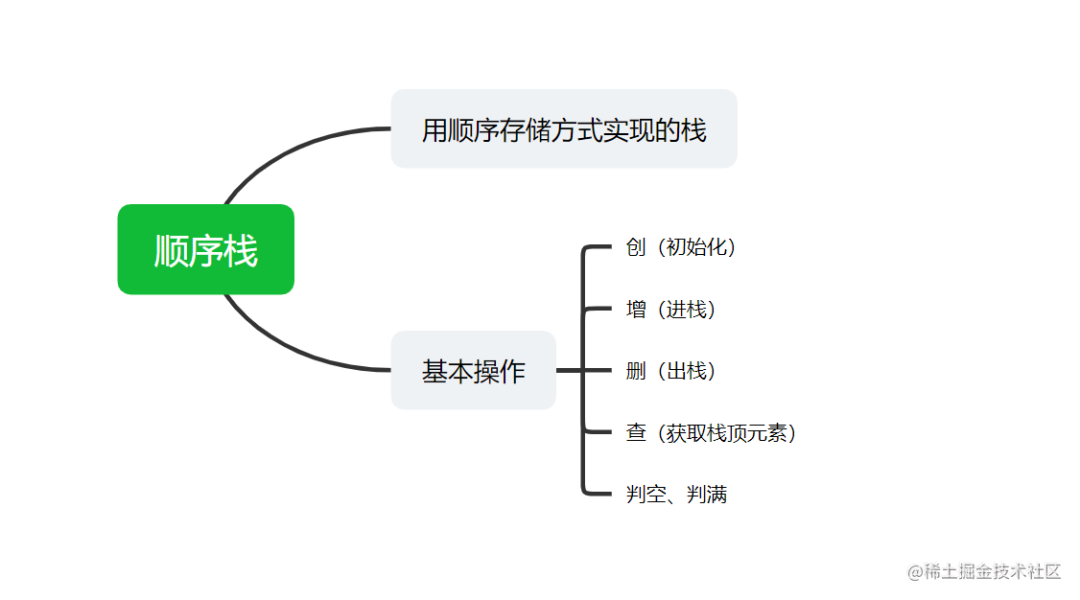
3.1 顺序栈的定义

#define MaxSize 10           //定义栈中元素的最大个数 
typedef struct{
 ElemType data[MaxSize];   //静态数组存放栈中的元素
    int top;      //栈顶指针
}SqStack;         //结构体重命名

声明一个顺序栈后就会在内存中分配一整片连续的空间，其中内存大小为：MaxSize*sizeof (ELemType)

void testStack(){
 SqStack S; //声明一个顺序栈
}

3.2 栈的初始化操作

由于栈顶指针 top 需要指向此时栈顶元素，所以让 top 指向 0 是不合理的，可以初始化让 top 指向 - 1; 判断一个栈是否为空，即判断 S.top 是否等于 - 1 初始化栈：

void Inittack(SqStack){
 SqStack S;   //声明一个顺序栈
 S.top=-1;
}

判断栈空：

bool StackEmpty(SqStack S){
    if(S.top==-1)      //栈空
        return true;
    else 
        return false;  //非空
}

3.3 进栈操作

分析：

判断栈是否为空

栈顶指针 + 1

新元素入栈

bool Push(SqStack &S,ElemType x){
 if(S.top==NaxSize-1)
        return false;
 S.top+=1;
 S.data[S.top]=x;
        return true;
}

3.4 出栈操作

bool Push(SqStack &S,ElemType &x){
 if(S.top==-1)
        return false;
    x=S.data[S.top--];
        return true;
}

3.5 读栈顶元素操作

bool GetTop(SqStack &S,ElemType &x){
 if(S.top==-1)
        return false;
    x=S.data[S.top];
        return true;
}

4. 共享栈

两个栈共享同一片空间

#define MaxSize 10           //定义栈中元素的最大个数 
typedef struct{
 ElemType data[MaxSize];   //静态数组存放栈中的元素
    int top0;     //0号栈栈顶指针
    int top1;     //1号栈栈顶指针
}SqStack;         //结构体重命名
初始化栈：
void InitStack(ShStack &S){
 S.top0=-1;
 S.top1=MaxSize;
}

5. 链栈的定义

进栈 / 出栈都只能在栈顶一段进行

链头作为栈顶

typedef struct Linknode{
 ElemType data;           //数据域
    struct Linknode *next;   //指针域
}*LiStack                    //栈类型定义

审核编辑：刘清