简述优化电磁线圈电流的3种方法

如果您想要设计电磁线圈， COMSOL Multiphysics® 软件的 AC/DC 模块与优化模块可以帮助您快速实现并进行迭代改进。今天，我们将研究如何进行线圈系统优化设计，并通过改变线圈的驱动电流来实现所需的磁场分布。还将介绍三种不同的优化目标和约束。如果您对线圈建模或优化感兴趣，这篇文章将满足您的好奇心！

磁场模型与优化问题陈述

我们今天要研究的问题是十匝轴对称线圈结构的优化，如下图所示。xy 平面两侧的五匝线圈中的每一匝都是对称但独立驱动的。

带有五个独立驱动线圈对的十匝线圈。目标是改变中心线处的磁场（绿色突出显示）。

线圈旋转轴对称，且关于 z=0 平面对称，因此我们可以将计算模型简化为二维轴对称模型，如下图所示。建模域被无限元域 截断。我们使用理想磁导体边界条件来模拟关于 z = 0 平面的对称性。因此，我们的模型简化为四分之一圆域，有五个独立的线圈，这些线圈使用线圈域 特征建模。

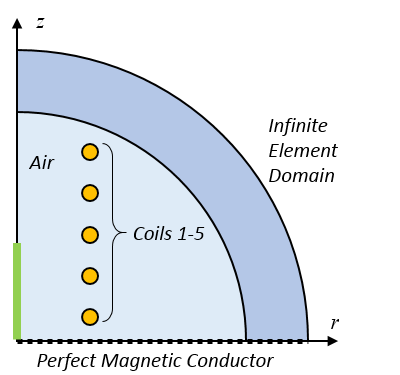
计算模型示意图。

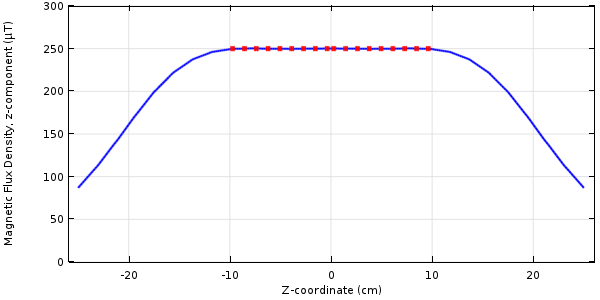
如果所有线圈都以相同的 10A 电流驱动，我们可以绘制沿中心线的磁通密度的 z 分量，如下图所示。我们想要通过优化来改变沿一部分中心线的场分布。

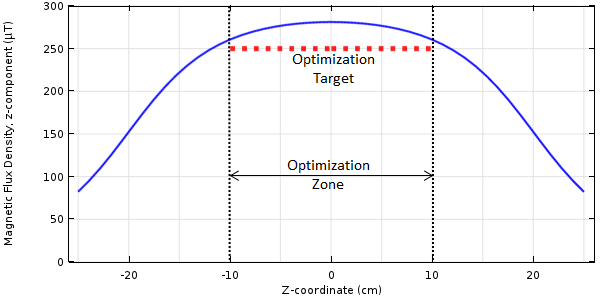
沿线圈中心线的磁场分布。我们希望在优化区域内磁场。

从上图可以看出，由于每个线圈的电流为 10A，我们可以看到沿着一部分中心线存在磁场。我们希望通过调整线圈电流来改变磁场分布。我们的控制变量是五个独立的线圈电流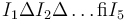：。这些控制变量有界限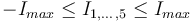：。也就是说，电流不能太大，否则线圈会过热。

我们将研究三种不同的优化问题：

1. 使中心线处的磁场尽可能接近期望的目标值
2. 最小化驱动线圈所需的功率，以及在几个点上对场最小值的约束
3. 最小化沿中心线的磁场梯度，以及在某一点上对场的约束

针对特定场值进行优化

我们用更数学化的语言描述这些优化问题。第一个优化问题可以写成：

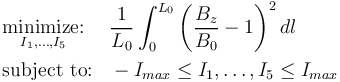
这里的目标是最小化计算得到的 Bz 与目标值之间的差异，其中目标值 B0 = 250μT，将 Bz 沿线圈中心线从 z = 0 到 z = L0进行积分。注意，该目标是相对于 L0 和 B0 归一化的。这样做是为了使这个目标函数的大小约为 1。对于任何优化问题，都应该对目标函数进行缩放。

现在，我们看看这个问题在 COMSOL Multiphysics 中的实现过程。我们首先在模型中添加一个优化 接口，该接口包含两个特征。第一个特征是全局控制变量，如下面的屏幕截图所示。我们可以看到设置了五个控制变量：I1,...,I5。这些变量用于通过磁场接口的五个线圈特征指定电流。

这些变量的初始值、上界和下界也由两个全局参数 I_init 和 I_max 指定。另请注意，比例因子 设置为控制变量的幅值也接近 1。在所有三个示例中，我们将对控制变量使用相同的设置。

设置全局控制变量特征，该特征指定线圈电流。

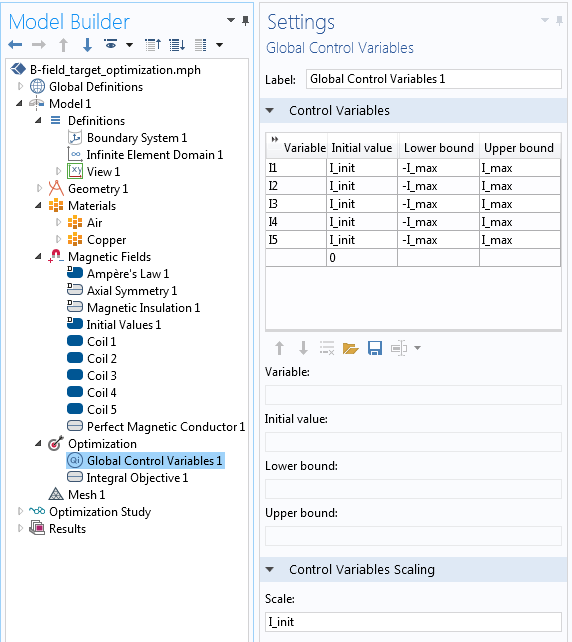
接下来，通过边界上的积分目标 特征定义目标函数，如下面的屏幕截图所示。请注意，没有勾选乘以 2πr 。

设置目标函数确保沿一个边界满足所需的场。

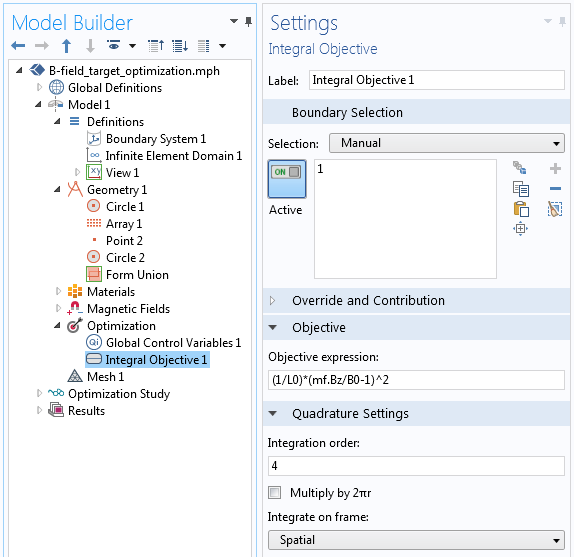
我们在研究中包含优化 步骤，如下面的屏幕截图所示。由于可以得到目标函数关于控制变量的解析梯度，因此我们可以使用 SNOPT 求解器。该求解器利用解析梯度，在几秒钟内求解优化问题。所有其他求解器设置都可以保留为默认设置。

优化研究步骤。

求解后，我们可以绘制场和结果。下图显示 Bz 场与目标值非常接近。

沿中心线优化磁通量目标值的结果。

通过场约束最小化功率

我们的第二个优化问题是最小化驱动线圈所需的总功率，并约束中心线上若干点上对场的最小值。这可以表示为：

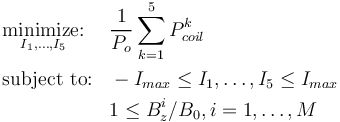
其中 Po 是所有线圈中消耗的初始总功率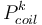，是第 k 个线圈中消耗的功率。

我们还希望将中心线上 M 个点处的场限制在 B0 值以上。

此问题的实现使用了与以前相同的“全局控制变量”特征。最小化线圈总功率的目标是通过全局目标 特征实现的，如下面的屏幕截图所示。每个线圈特征中功率的内置变量（mf.PCoil_1,...,mf.PCoil5）可以直接使用。目标相对于初始总功率进行归一化，使其接近统一。

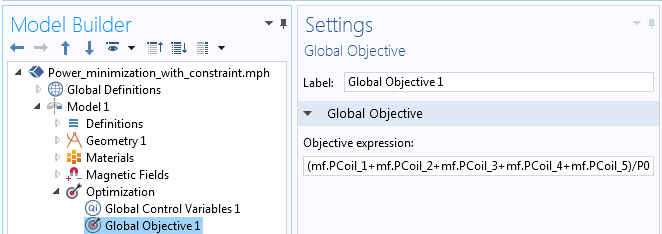
实现将总功率降至最低的目标。

对场最小值的约束必须在模型中的一组离散点上实现。本例中，我们引入了优化区域上均匀分布的五个点。必须使用单独的点总和不等式约束 特征引入每一个约束，如下所示。我们再次应用归一化，使得此约束的大小为 1。请注意，不勾选乘以 2πr 选项，原因是这些点位于中心线上。

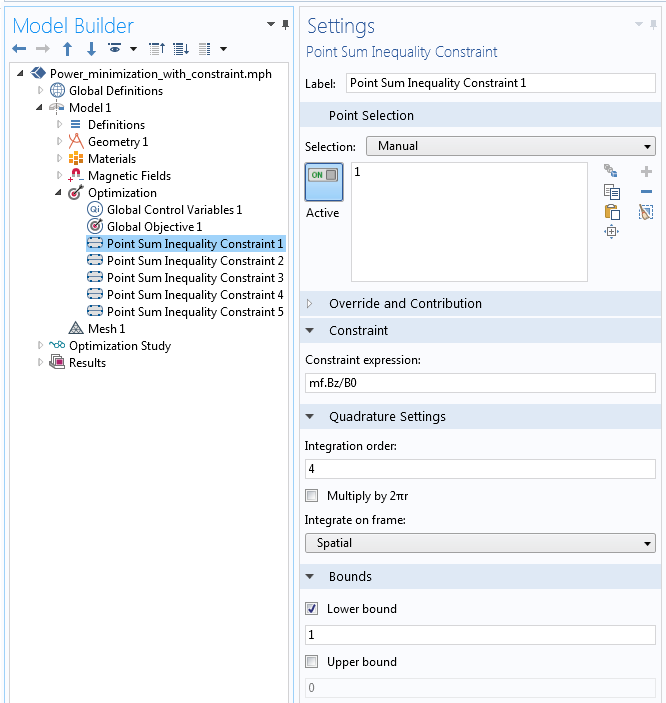
在某一点上实现对场最小值的约束。

我们可以使用与以前相同的方法解决这个问题，结果如下图所示。值得注意的是，最小功率解下目标区域上常分布为非均匀的。

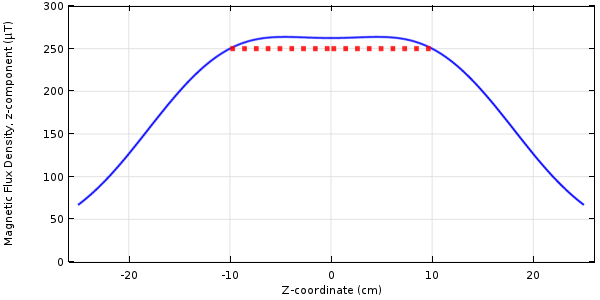
通过对场最小值的约束来优化最小功耗的结果。

通过场约束最小化梯度

最后，我们考虑最小化沿着优化区域的场梯度，在中心点对场进行约束。这可以表示为：

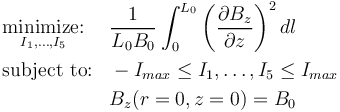
这里的约束线圈中心点处的场。尽管优化 接口确实有明确的等式约束，但我们可以使用具有相等上界和下界的不等式约束来实现相同的结果。我们再次应用归一化，这样我们的约束实际上为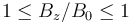，如下图所示。

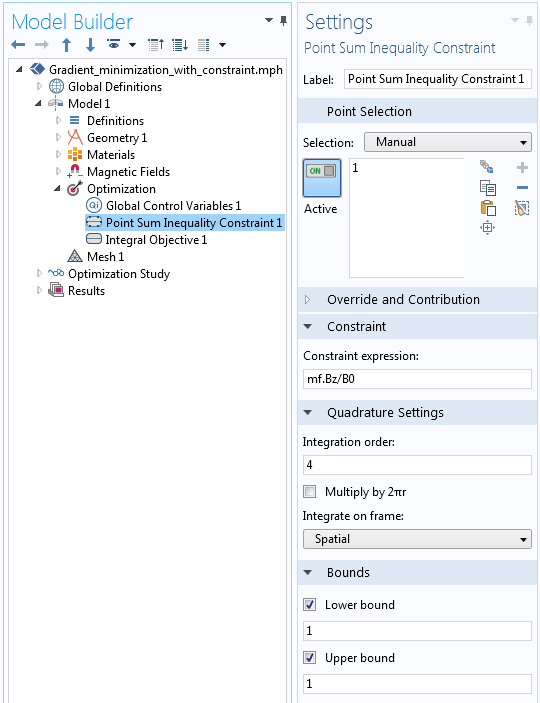
实现等式约束。

最小化目标区域内场梯度的目标是通过“积分目标”特征实现的（如下所示）。Bz 场相对于 z 方向的梯度是用导数算子 d(mf.Bz,z) 计算的。

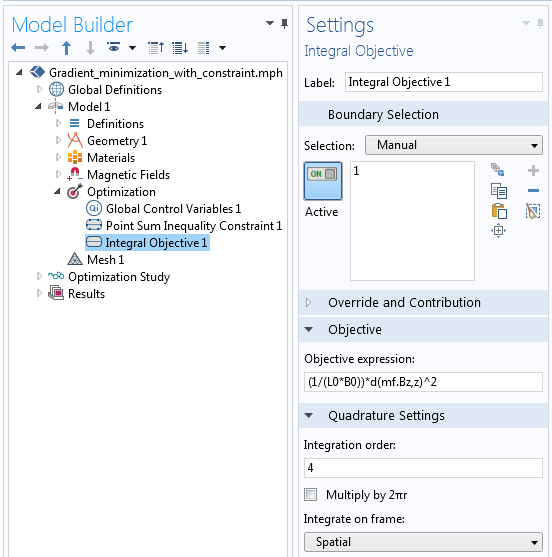
最小化场梯度的目标。

我们可以使用与以前相同的求解器设置。本例的结果如下所示。优化区域内的场非常均匀，并且与中心点的目标相匹配。

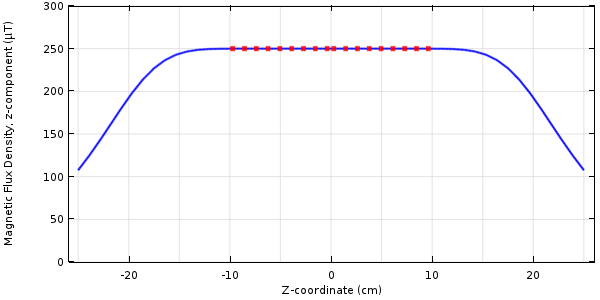
对某一点的场有约束的最小场梯度进行优化的结果。

虽然这里的场看起来与第一种情况几乎相同，但线圈电流的解却截然不同，这就引出了一个有趣的问题。线圈电流有多种组合，可以在最小化场差或梯度方面给出几乎相同的解。另一种说法是，目标函数有多个局部最小点。

SNOPT 优化求解器使用一种基于梯度的方法，并针对线圈电流的不同初始条件接近不同的局部最小值。虽然基于梯度的求解器会收敛到局部最小值，但不能保证这实际上是全局最小值。一般来说（除非我们对设计空间进行彻底的搜索），永远不可能保证优化的解是全局最小值。

此外，如果我们要增加这个问题中的线圈数量，我们可以得出线圈电流的多种组合几乎等同于最优的情况。也就是说，设计空间（线圈电流的组合）中没有单个最佳点，而是几乎相等的“最佳线”或“最佳表面”。优化求解器不提供直接反馈，但在这种情况下往往会收敛得更慢。

结束语

本文我们介绍了三种不同的方法来优化流经不同匝线圈的电流。在这三种方法中，我们引入了不同类型的目标函数和约束，它们也可以适用于其他各种情况。根据线圈设计问题的整体目标和目的，您可以使用其中任何一个，甚至是完全不同的目标函数和约束集。这些示例表明了 COMSOL 优化模块与 AC/DC 模块结合使用的强大功能和灵活性。