Vladimir Vapnik创立支持向量机

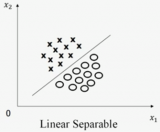
在Vladimir Vapnik创立支持向量机前，已有如下结论：在二分类情况中，如果一个数据集线性可分，即存在一个超平面可将两个类别完全分开，那么一定存在无数个超平面将这两个类别完全分开。

在特征空间为二维平面时，分类训练数据的超平面的具体图形为直线，下文介绍在无数个此类直线中选择可使分类效果最优的直线。

一、直观感觉分类效果最优的直线

如图一左图所示，有三条直线可将图一左图中的圆圈和叉分为两类，该三条直线分别为1号线、2号线、3号线。在选择可使圆圈和叉分类效果最优的直线（下文简称“最优分类直线”）时，可能多数人会选择2号线。但根据免费午餐定理，在未假设训练数据的先验分布的情况下，三条直线对于圆圈和叉分类效果相同。人的直观感觉似乎和免费午餐定理产生矛盾。

其实，似乎矛盾的原因是人们在选择最优分类直线时，已对训练样本的先验分布做出假设。例如，多数人选择2号线为最优分类直线可能的假设为训练样本的位置在空间中具有测量误差（选择2号线为最优分类直线的先验分布假设不唯一）。

如图一右图所示，如果红色实线圆圈的位置分布具有测量误差，其实际位置处于虚线圆圈位置，那么1号线的分类效果不如2号线的分类效果；如果红色叉的位置分布具有测量误差，其实际位置处于虚线圆圈位置，那么3号线的分类效果不如2号线的分类效果，即2号线更可抵御训练样本误差，因此，在训练样本的位置在空间中具有测量误差的先验假设下，2号线为最优分类直线。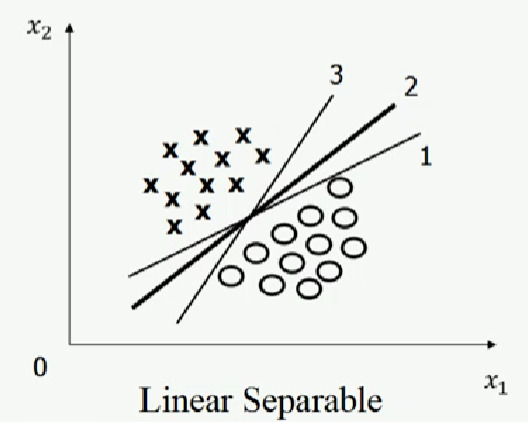





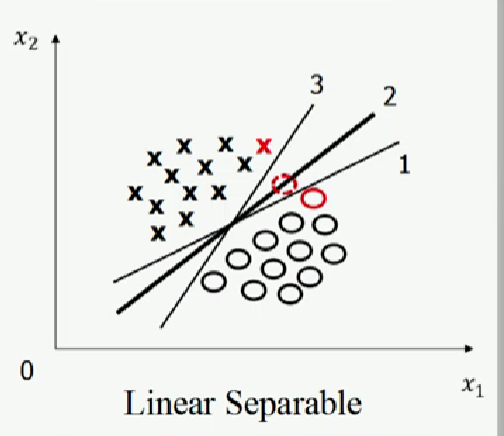
图一，图片来源：中国慕课大学《机器学习概论》

二、寻找最优分类直线

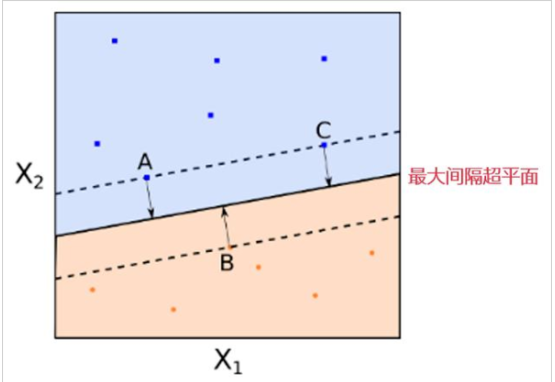
Vladimir Vapnik基于最优化理论，对寻找最优分类直线的回答如下：任意一条可将圆圈和叉完全分类的直线向一侧平行移动，直至其穿过一侧一个或几个训练样本；再向另一侧平行移动，直至其穿过另一侧一个或几个训练样本。如图二所示，定义被穿过的数据（图二中的红圆圈和叉）为支持向量（Support Vector），定义穿过圆圈和叉的直线间的距离为间隔，则最优分类直线为间隔最大的直线。



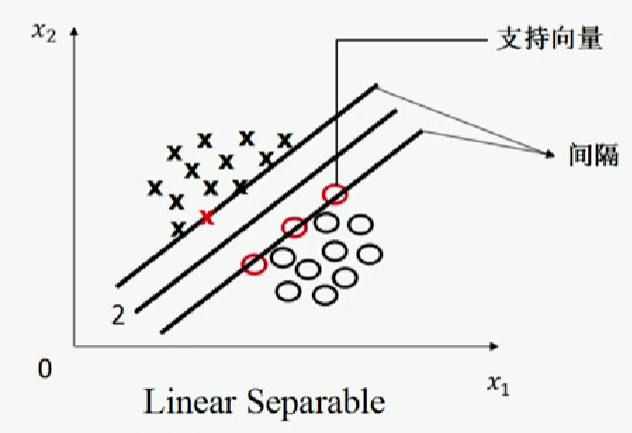
图二，图片来源：中国慕课大学《机器学习概论》

根据Vladimir Vapnik的回答，因为前文所述问题中的2号线的间隔最大，所以2号线为最优分类直线。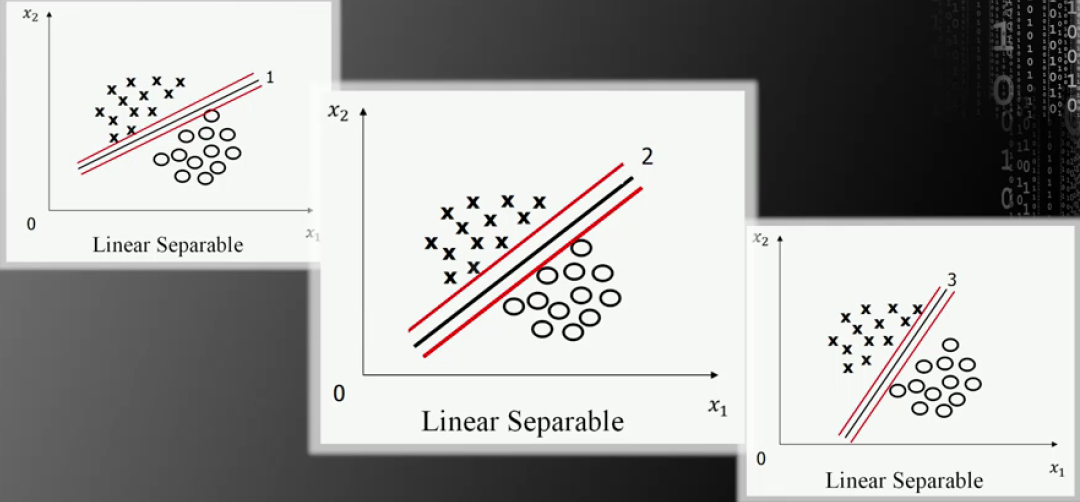



图片来源：中国慕课大学《机器学习概论》

但仅根据间隔最大不能得出唯一的最优分类直线，例如，前文所述问题中，所有与2号线平行的线均为间隔最大的直线。因此，为可得出唯一直线，最优分类直线被限定处于穿过两侧支持向量的两条直线中间的直线，即最优直线与两侧支持向量的距离相等。

综上，支持向量机寻找的最优分类直线应满足：

（1）该直线可将训练数据完全分为两类。

（2）该直线可最大化间隔。

（3）该直线处于间隔的中间，其与所有支持向量的距离相等。

审核编辑：刘清