在此我们以绿皮书中的例子为说明。
rand bit x; rand bit[1:0] y;
without order, solve before的概率分布
在此设计三种不同的随机先后顺序,分析x和y取值的其概率分布。
1. without order:
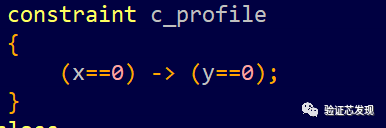
在x和y互相耦合的约束下,{x,y}的合法取值共有5种,每种取值的概率分别为1/5。
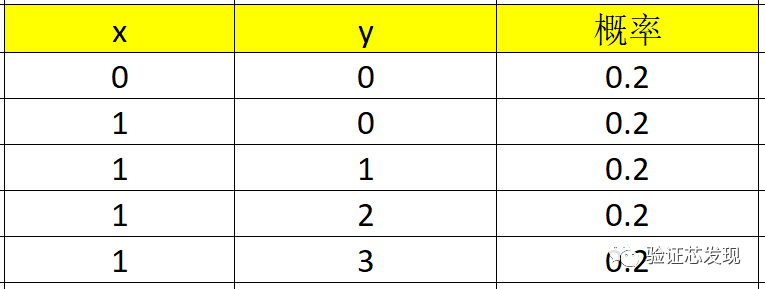
因此,x=0的取值概率为:0.2,y=0的取值概率为:0.2+0.2=0.4,y=1,2,3的取值概率都是0.2。这种分析方式也是符合SV语法手册的说明,参见SV语法手册第18.5.10小节的说明。
注:这种概率的分布和绿皮书中的分析并不相同,这是由于绿皮书中采用vcs仿真器不同版本的差异造成的。在较新的vcs版本中,有ntb_solver_mode仿真选项,在设置ntb_solver_mode=1时,可以得到绿皮书中的结果;ntb_solver_mode=2或者使用默认设置,得到的就是上面的分析结果。
2. solve x before y:
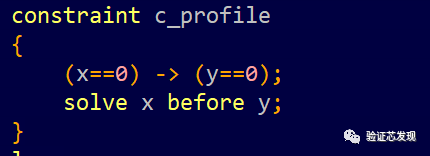
solve-before并没有改变合法解的空间,只是改变了概率分布,由于x先于y求解,因此x的随机不受y取值的影响,其概率分布如下:
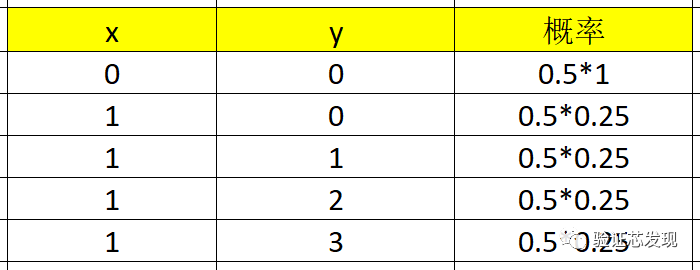
因此,x=0和1的取值概率都是0.5,y=0的取值概率为:0.5+0.125=0.625,其余取值概率都为0.125。
3. solve y before x:
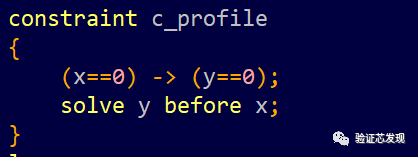
和第2点类似,概率分布如下:
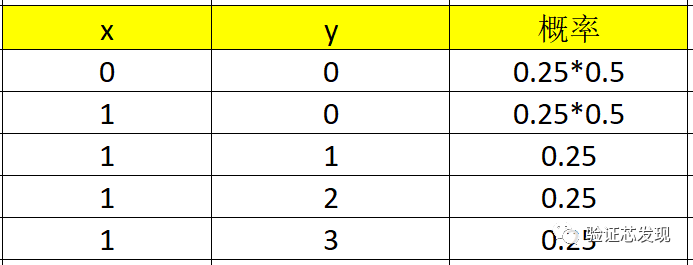
因此,y的取值是均匀分布,都是0.25,x=0的取值概率都是0.125,x=1的取值概率为:0.25*3+0.25*0.5=0.875。
上述三种约束,使用vsim仿真,提取x和y的取值概率分布如下:
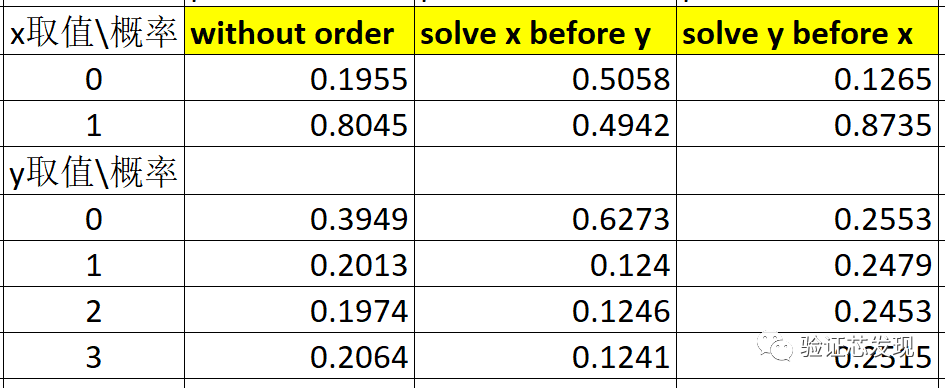
因此,无论是选择哪一种约束顺序,由于x和y之间存在耦合,二者的取值概率都不会同时满足各自的均匀分布,即x=0/1:0.5和y=0,1,2,3:0.25不能同时出现。
进一步,如果上述的约束中,如果指定了x或者y的概率分布,结果又会如何?
指定x的概率分布:without order, solve before的差异分析
添加x的dist概率分布,分别对without order,solve_before方式进行测试。
without order:
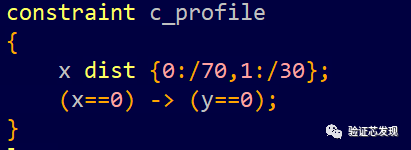
solve x before y:
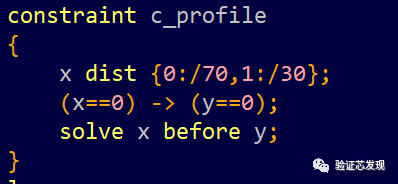
solve y before x: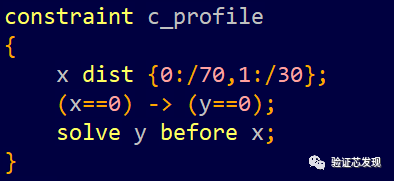
测试结果如下: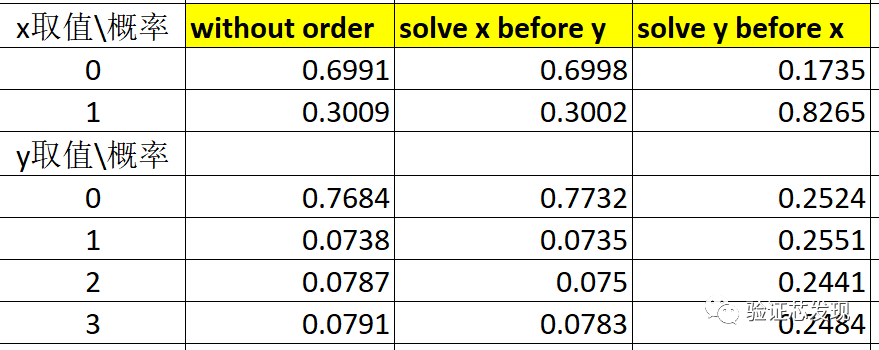
上表实测结果的理论分析值如下:
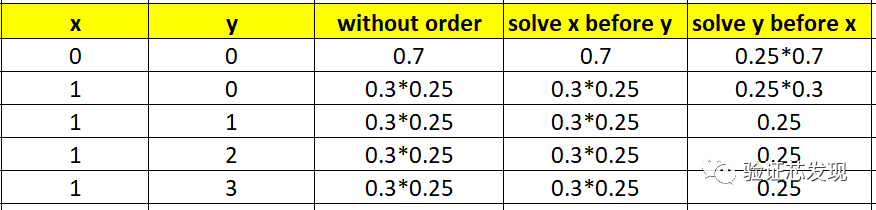
从中可以看出:
(1)在without order和solve x before y条件下,x的dist概率分布会得到满足;
(2)在solve y before x的条件下,优先满足solve before顺序,y是均匀分布;
指定y的概率分布:without order, solve before的差异分析
添加x的dist概率分布,分别对without order,solve_before方式进行测试。
without order:
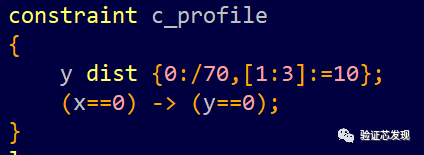
solve x before y:
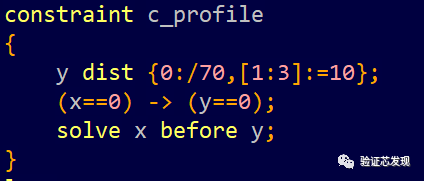
solve y before x:
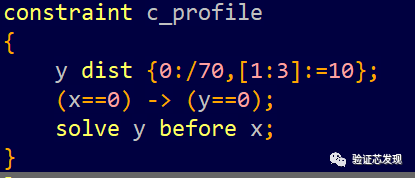
测试结果如下:
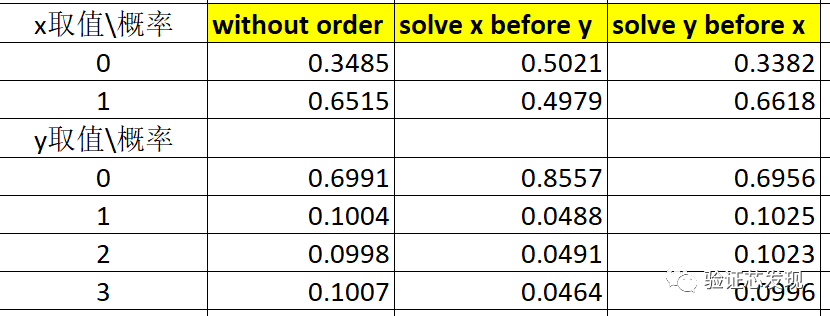
上表实测结果的理论分析值如下:
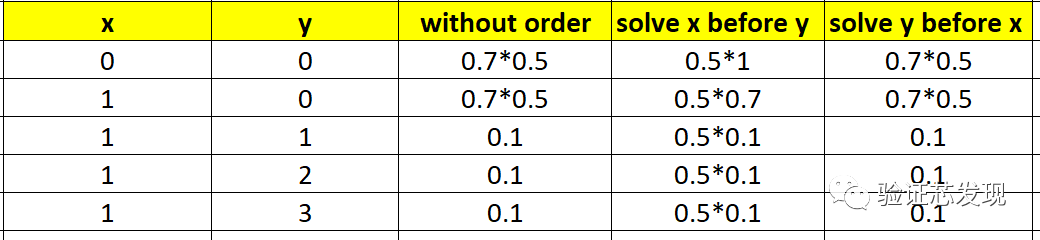
从中可以看出:
(1)在without order和solve y before x条件下,y的dist概率分布会得到满足;
(2)在solve x before y的条件下,优先满足solve before顺序,x是均匀分布;
同时指定x和y的概率分布:without order, solve before的差异分析
添加x的dist概率分布,分别对without order,solve_before方式进行测试。
without order:
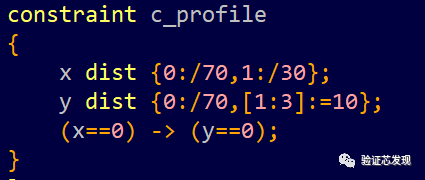
solve x before y:
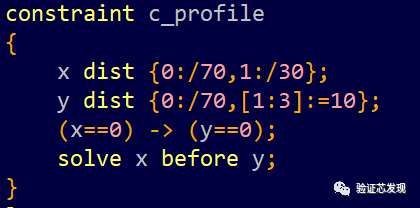
solve y before x:
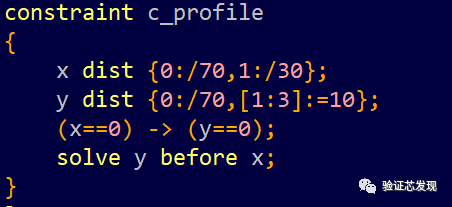
测试结果如下:
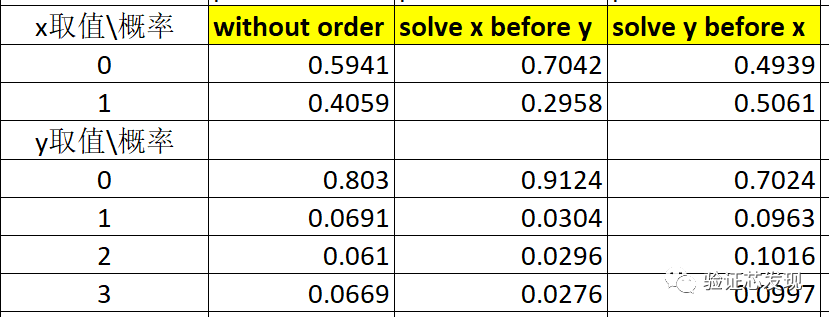
上表实测结果的理论分析值如下:
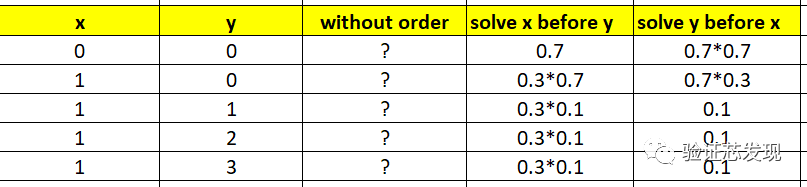
从中可以看出:
(1)solve before 仍会优先得到满足;
(2)在同时指定dist概率分布时,without order的概率理论值分析方法暂时没有确定,同时也没有和测试值吻合。
总的来看,使用->或者if-else时,参数的概率分布会变得复杂且不易理解,尤其涉及到多条件蕴含时,某些参数的概率分布很难做出预期,因此更加需要后续的功能覆盖率加以分析,找出不合理的约束。
审核编辑:刘清
-
仿真器
+关注
关注
14文章
1018浏览量
83739 -
Verilog
+关注
关注
28文章
1351浏览量
110091
原文标题:systemverilog 随机约束implication的概率分析
文章出处:【微信号:处芯积律,微信公众号:处芯积律】欢迎添加关注!文章转载请注明出处。
发布评论请先 登录
相关推荐
概率随机数生成【子模块】
设计验证中的随机约束
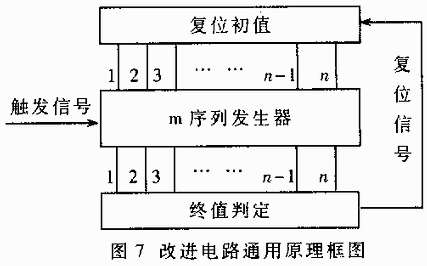
M序列伪随机码在测距回答概率控制中的应用




 systemverilog随机约束implication的概率分析
systemverilog随机约束implication的概率分析










评论