FFT快速傅立叶变换的工作原理

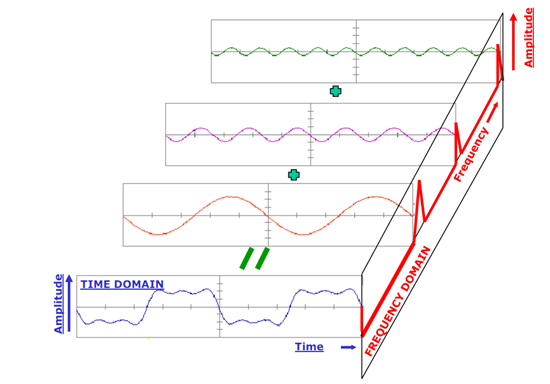
FFT是计算DFT的快速算法，但是它是基于复数的，所以计算实数DFT的时候需要将其转换为复数的格式，下图展示了实数DFT和虚数DFT的情况，实数DFT将时域中N点信号转换成2个(N/2+1)点的频域信号，其中1个(N/2+1)点的信号称之为实部，另一个(N/2+1)点的信号称之为虚部，实部和虚部分别是正弦和余弦信号的幅度。

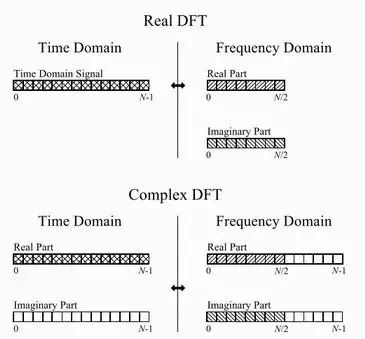
相比较而言，复数DFT将2个N点的时域信号转换为2个N点的频域信号。时域和频域中，1个N点信号是实部，另1个N点信号是虚部。

如果要计算N点实数DFT，则将这个N个点作为时域中的实部，另取N个0点作为时域的虚部，用FFT计算这样一个复数信号的DFT得到2个N点的频域信号，1个N点是实部另1个N点是虚部，在这两个N点的信号中，从0到N/2个点就是须计算的N点实数的DFT频域。

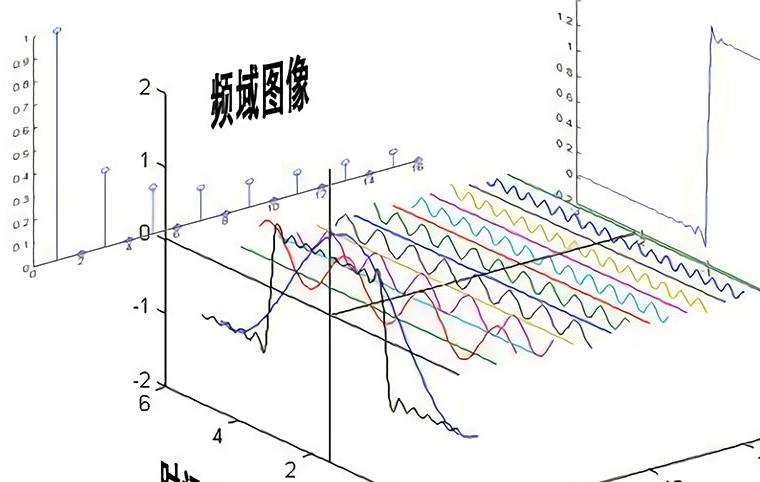
对于实数DFT来说，它的频域也是离散周期信号，其周期为N点，从0到N/2点和1-N到-1点具有对称性，这个你可以从下面一张图看出。图中坐标不是用N表示，是用采样频率的分数表示。

所以你如果用FFT反变换计算的是实数时域，则要满足上图的对称性。

FFT如何工作

◤

FFT的计算可以分为三步：首先将1个N点的时域信号分成N个1点的时域信号，然后计算这N个1点时域信号的频域，得到N个频域的点，然后将这个N个频域的点按照一定的顺序加起来，就得到了我们需要的频谱。这里每个点的意思是复数，都有实部和虚部。

• 第一步的信号分解按照下面的规律执行：

可以看出它是按照比特反转顺序来分解的。

• 第二步是计算每个点的频谱：

这一步很简单，因为一个时域的点的频谱的数值就是它自己，所以这一步什么也不需做，但需明白这时候N个点不是时域信号了，而是频域信号。

• 第三步是将这N个频域信号结合起来

这一步是最麻烦的一步。就是和前面时域分解的顺序相反，将2个1点的频域信号变成1个2点的频域信号，再将2个2点的频域信号变成1个4点的频域信号，一直到结束。这里看下如何将2个4点的频域信号变成1个8点的频域信号。

首先对1个4点的频域信号进行复制，这样能稀释时域信号，也对另1个4点的频域信号进行复制，不过复制之前需要乘上正弦函数，这样得到的稀释时域信号时经过了平移的，然后将这两个频域信号加起来，如下图所示。之所以这么做的目的是在时域分解的时候就是用这种交织的分解方式的。

以下是基本的运算，称为蝶形运算，它将2个1点的复数变成1个2点的复数。

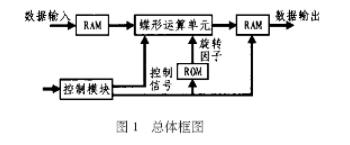
FFT运算的流程图

运算速度比较

• 如果用相关方法计算DFT：

• 如果用FFT方法计算DFT：

不过，FFT的速度还能更快。 比如使用基4或者基8，这样不是2点一计算，而是4点或者8点一计算，可以提高速度。

FFT对DSP来说就像是晶体管对电子学来说，都是领域的基础，每个人都知道怎么使用它们，但是只有很少一部分真正了解它们的原理。

事实就是这样，你只要知道怎么用就可以了。