通常我们分析的信号是一个纯实数信号,没有虚部。经典的例子当然是用正弦波。当我们用傅立叶变换分析,通常是FFT算法,分析信号时,绝大多数人都知道我们将得到的频率结果位于0Hz到奈奎斯特频率(采样频率的一半)之间。同时也明白相应的FFT输出结果是复数形式,因此可以用幅值和相位形式或实部和虚部形式表示。
出于解释目的,假设我们使用的正弦波的频率为128Hz,幅值为5,初相位为60度。信号的开始部分如图1所示。现在假设我们以1024个样本点每秒的速率对这个信号采集了4s的数据。显然,这些样本点稍微人为地作了些选择,为了避免截取成非周期信号,并且要确保信号的频率正好与FFT的某一条谱线重合。
对这个信号进行常规的FFT计算,得到幅值和相位形式的结果如图2所示。
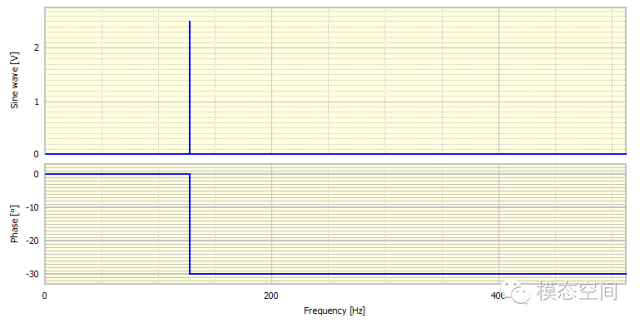
图2 FFT的半谱
注意到计算得到的幅值是2.5,刚好是原信号幅值的一半。这从数学上是正常的,将在后面进行说明。然而,一些商业软件给出的结果幅值是5,这是因为这些软件自动对FFT结果进行加倍。我们也注意到相位是-30度,但我们开始使用的正弦波的初相位是60度。但这-30度却是正确的,这是因为FFT是用余弦定义实部,正弦定义虚部。因此,FFT的0度,用作余弦波在正峰开始时的参考。因此,初相位为60度的正弦波与初相位为-30度的余弦波是相同的。
从数学上,有
sin(60)=sin(90-30) =sin(90)cos(-30)+cos(90)sin(-30)=cos(-30)
展示的频率范围0到奈奎斯特频率经常被称作半范围的傅立叶变换。这是一个全范围的变换,我们可以选择的范围从0至采样频率,或者从负奈奎斯特频率到正奈奎斯特频率(-采样频率/2至+采样频率/2)。后一种形式实际上更易于解释,同时包含了负频率的概念,这似乎初看起来更直观。实际上的确非常直观,让我们回顾一下基本知识。
按常规,正旋转是按逆时针方向。如果我们观察一个向量的端点以角频率ω旋转,那么相应的轨迹为正弦波Asinωt=Asin2**π ft 。 波形的过去和未来为图所示。
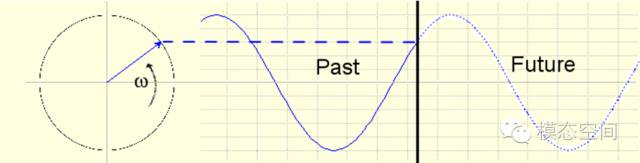
图3 逆时针方向旋转的向量
假设我们现在观察相同的设置,但现在这个向量按顺时针方向旋转。
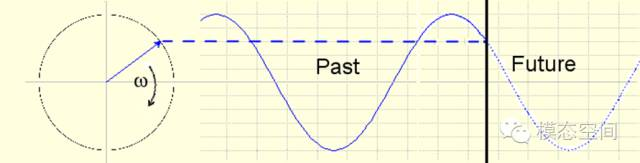
图4 顺时针方向旋转的向量
两个波形实际上是相同的。因此,如果我们测量这个正弦波,我们不知道波形何时开始,我们也不能确定它是否是顺时针方向还是逆时针方向。实际上,正频率相当于逆时针方向旋转,负频率相当于顺时针方向旋转。由测量到的实数信号,我们不同区分出正负频率。
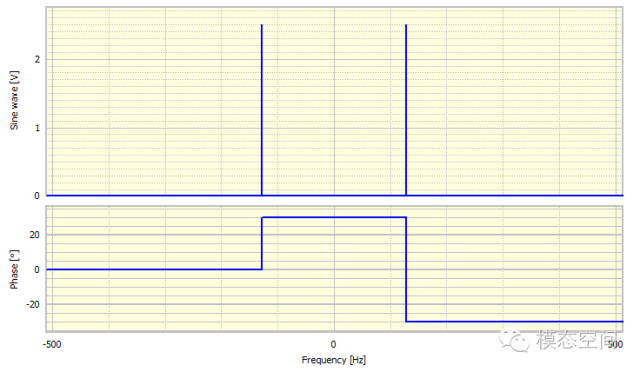
图5 全范围的FFT
假设现在我们要对相同的正弦波进行一个从-采样频率/2至+采样频率/2有全范围的FFT计算。给出结果如图5所示。这有两个分量,二者的幅值为2.5,但一个是负频率-128,相位为+30度,另一个为+128Hz,相位为-30度。这二者组合得到了开始时的正弦波。对于一个纯实数信号而言,负频率的幅值是正频率幅值的镜像,而相位镜像成负值。因为我们能从正频率部分完全预测出负频率部分的幅值和相位,因而,没有必要去计算负频率,因为它们并不包含更多的信息。
从数学公式上用幅值 A ,相位 ɷ ,描述一个信号
Ae ^iɷ^ =A(cos ɷ +isinɷ),而ɷ=2πf+θ
因此,我们有正频率成分
Acos (2πf-30)+i Asin (2πf-30)
和负频率成分
Acos (-2πf+30)+i Asin (-2πf+30)
因此,整个信号有
Acos (2πf-30)+i Asin (2πf-30)+ Acos
(-2πf+30)+i Asin (-2πf+30)
我们记得
cos (-ɷ)= cos (ɷ)
sin(-ɷ)=-sin(ɷ)
因此,我们可以将负频率成分写成
Acos (2πf-30)-i Asin (2πf-30)
将信号的整个表达示进行化简,得到
2Acos (2πf-30)=2Asin (2πf+30)
这表明,信号的相位与正频率成分的相位相同,幅值2倍于正频率成分的幅值。
-
奈奎斯特
+关注
关注
0文章
9浏览量
9293 -
傅立叶变换
+关注
关注
3文章
105浏览量
32566 -
FFT算法
+关注
关注
0文章
31浏览量
13460
发布评论请先 登录
相关推荐
半导体参数分析仪的FFT分析
FFT的幅值对应的频率点不对
讲座3 负频率
DFT算法与FFT算法的优劣分析
应用FFT对信号进行频谱分析
按频率抽取的FFT算法
论频谱中负频率成分的物理意义
FFT的分析和Xilinx FFT核的介绍
基于LabVIEw的FFT设计应用





 什么是FFT分析的负频率
什么是FFT分析的负频率
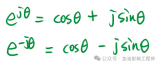










评论