开关电源环路稳定性分析(十一)

大家好，这里是大话硬件。

这篇文章主要是分享如何用观察法直接写出补偿网络中的零极点的表达式。

在前面的文章中，我们分别整理了OTA和OPA型的补偿网络，当时有下面的结论。

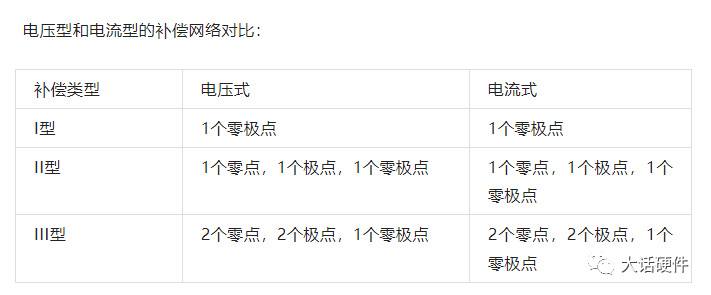
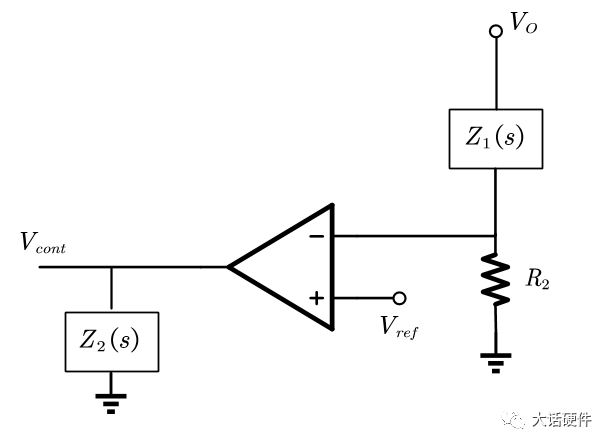
针对某个固定的补偿网络，我们可以用数学的方法推导补偿网络的零极点。 比如下面OPA的I型补偿网络，求解零极点的过程如下：

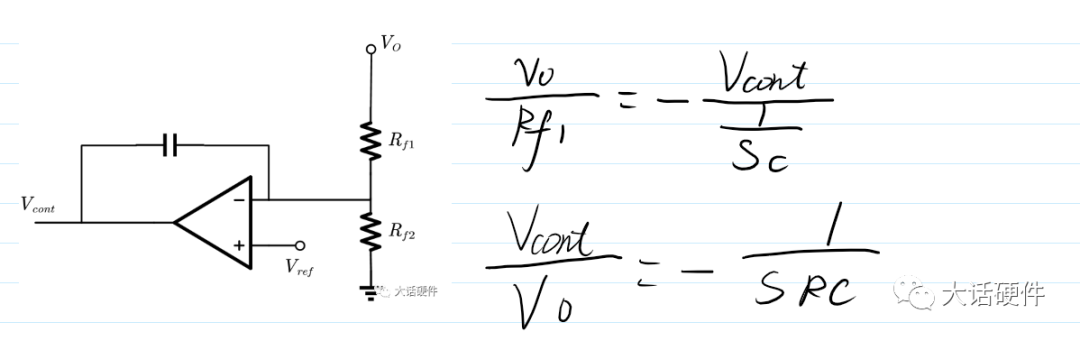
上面是纯粹数学方式求解的结果，从结果可以看出I型补偿只有极点，没有零点，相对来说还算简单。

下面求解II型补偿器的传递函数，写成标准零极点的形式：

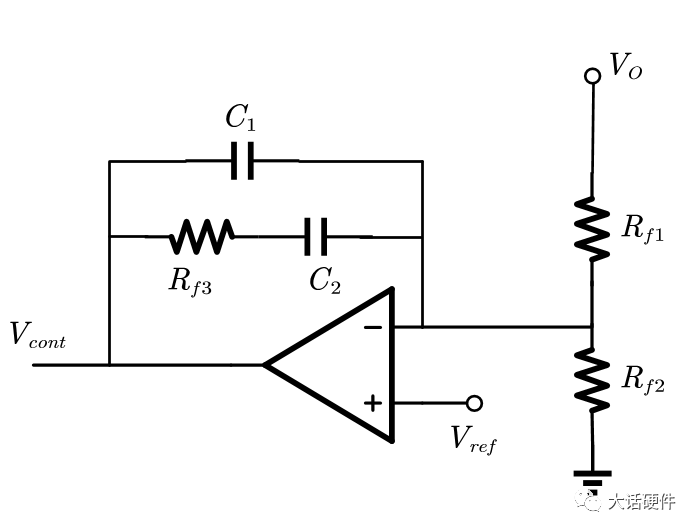
从上面的求解过程来看，是相当的复杂，而且这还是II型的补偿，换成III型的补偿，这个求解的过程会更复杂！

不信你看下面这个III型的补偿器，求解出的传递函数

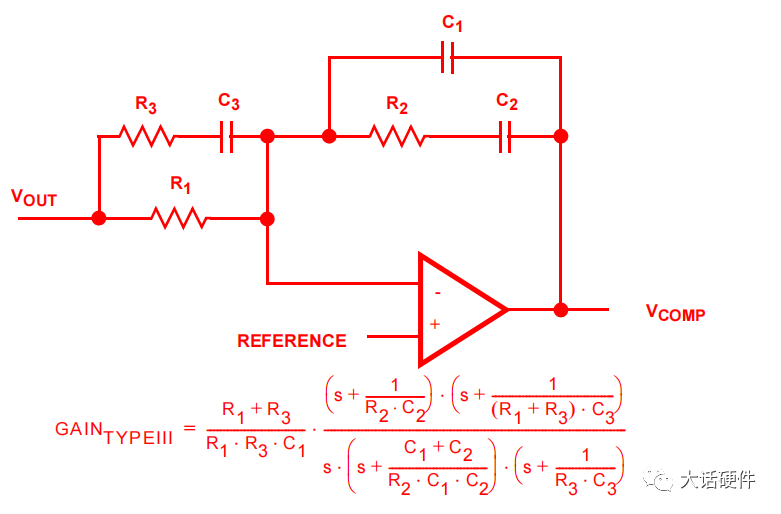
这是人家整理好的表达式，可以直接看出直流增益，零极点的位置。 如果要是自己求解的，按照上面II型的方法，至少需要10分钟才能求解出来一个，而且还不一定对。

最近在开关电源大牛巴索的书里面找到一种简洁的方法求解零极点的方法，因此结合前面我自己都认为很复杂的过程，来看下这种简单的方法。

书中以一个简单的串并联电路为例：

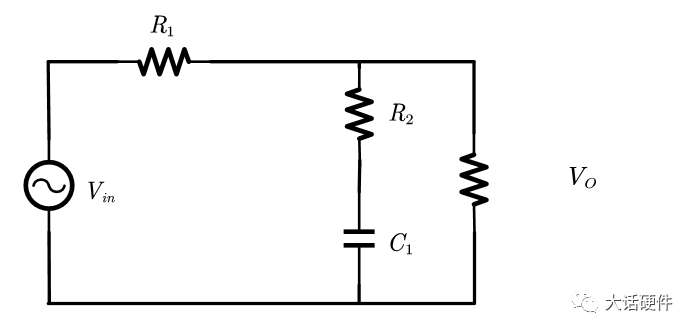
对于这个网络，开始没人知道这个传递函数有几个零极点，也不知道是否存在零点和极点，但是由于只有电容一个存储元件，最后传递函数的表达式可以写成如下的结构：

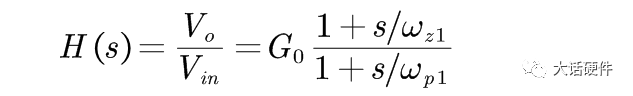
下面就是根据电路的性质，直接写成G，Wz，Wp的值，那么就可以得到传递函数的零极点。

首先是求解直流增益，即s=0，此时电容相当断开，所以G可以求出：

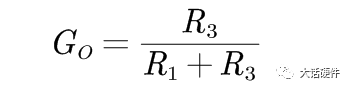
其次是求解零点，零点的定义是让激励信号永远不能到达输出的频率点，基于这个逻辑，我们需要找到电路中能阻止激励信号往输出传递的器件。

作者在书中提到了两种可能性：信号串联的时候，器件在这个频率点的阻抗的无穷大，或者这个器件在这个频率点将信号连接到地上形成短路。

基于以上两点作为前提，我们再看上述的网络：

电容C是输出端的以并联的形式的加入，这是要满足两种可能性中的一种，只有一种情况，那就是R2+C1的阻抗为0，此时传递函数的分子为0。

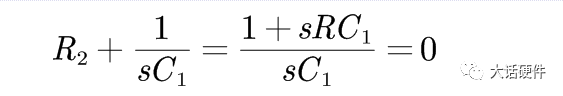
可以求出零点的位置

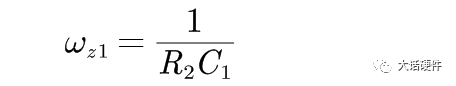
最后是求解传递函数的极点，求解极点的方法作者在书中介绍的是电路拓扑的时间常数，在求解的时候，电压源短路，电流源是开路，有点类似求解等效电阻的意思。

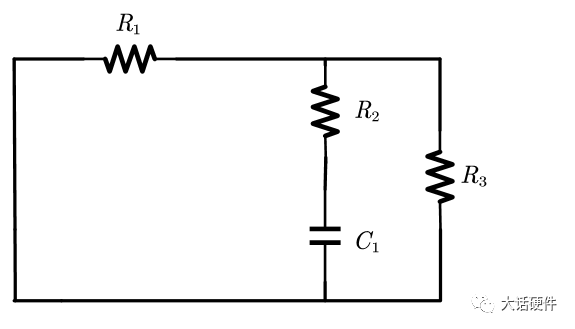
时间常数：

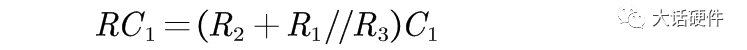
对于一阶系统，极点等效时间的常数，因此可以直接推导出极点：

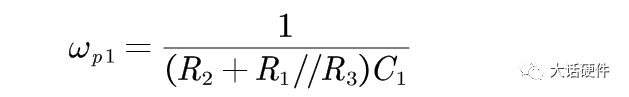
所以系统的传递函数为：

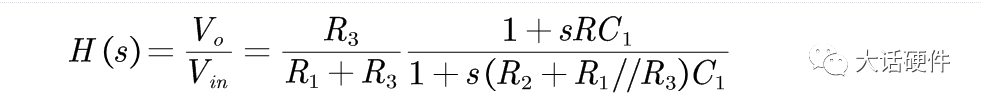
如果不用作者的方法，我自己也推导了一下，过程如下：

推导的过程明显比作者说的观察法难很多！！！

有了上面的内容，我们将上述的结论用在有补偿网络的传递函数里面。

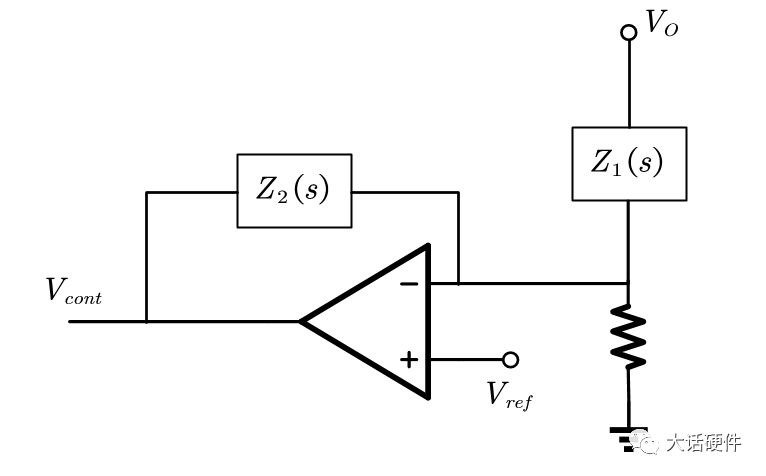
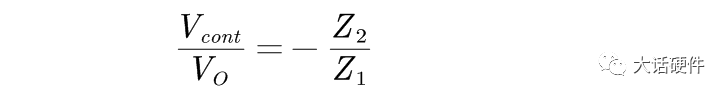
下面用前面的的理论来推导I型补偿网络的零极点:

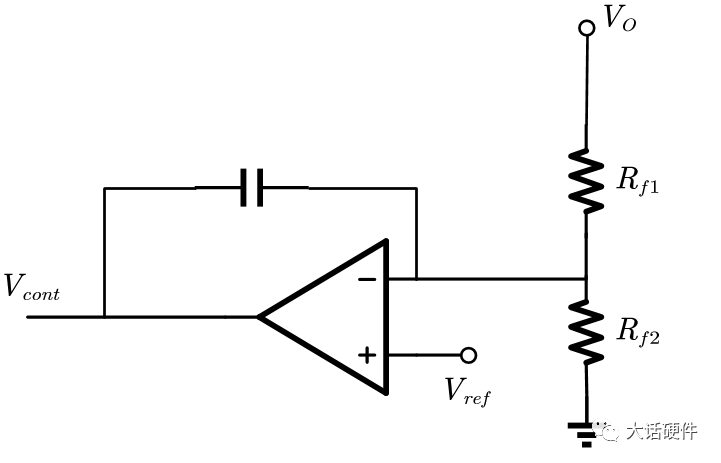
零点，输出为0，分,子为0，则Z2=0，则1/Sc=0，则频率为无穷大，实际中确定RC参数，频率不可能无穷大，因此，I型补偿 网络没有零点。

极点，时间常数，Rf1C，所以存在极点：

推导II型补偿网络的零极点

零点，输出为0，分子为0，则Z2=0，要使Z2的阻抗为0，C1的阻抗不能为0 ，只有RF3和C2的阻抗为0，因此，此时存在一个零点：

极点：极点是分母为0，在一阶系统中是求解电路网络结构的时间常数，而在在二阶系统中此种方法无法用。 此时，可以借鉴零点的求法，极点的定义是让传递函数的分母为0，则整个系统的值为无穷大，那么Z2的阻抗为无穷大。

（1）当频率为0时，电容C1的阻抗为无穷大，此时存在零极点

（2）当频率为0时，电容RF3和C2的阻抗为无穷大，此时存在零极点

上述两个零极点的频率都是在频率为0，因此是同一个零极点

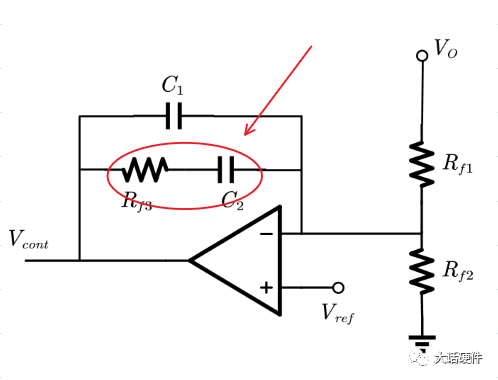
（3）当频率为f时，电容C1和RF3以及C2的串并联阻抗无穷大，除了频率为0的时刻，还存在另外一个频率f，即 Rf3+C2+C1的阻抗一起为无穷大

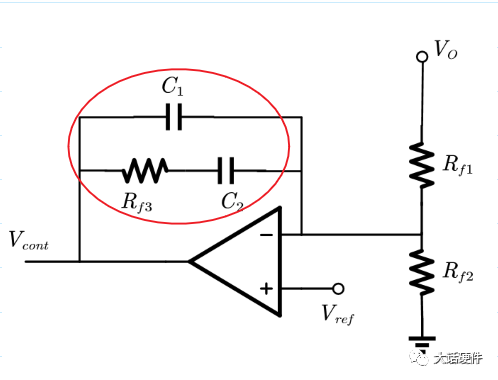
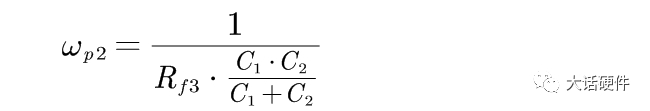
推导III型补偿网络的零极点

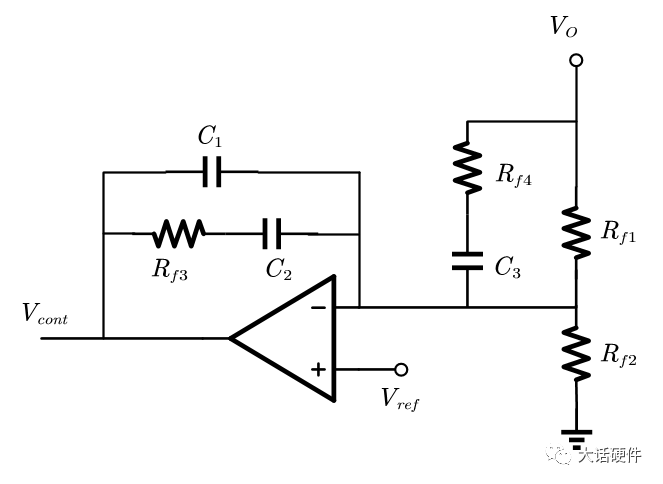
III型补偿相比II型补偿增加了一个电阻电容，推导方式和前面基本一致，但是增加的RF4，C3和电阻RF1之间可以有两种类型的组合。

当Rf4+C3阻抗为0时，系统增加一个极点，这样的频率是存在的，因此此时的极点为

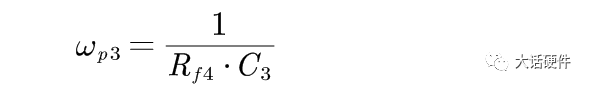
同理，Rf4+C3+RF1的阻抗为无穷大时，系统增加了一个零点，此时的零点

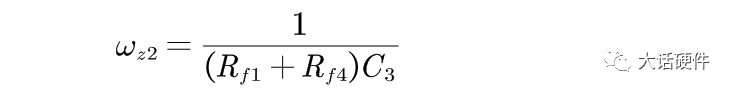
III型的另外几个零极点和II型的一样，这里不赘述。

上面的方面可以很快确定零极点，但是对于静态增益无法求出。 对于复杂的系统，求解传递函数比较困难时，通过这种方法可以很快看出零极点。 但是没办法将整个传递函数形式表达清楚，所以方法有利有弊。