算术运算
整数的算术运算也不总符合我们的常识,比如下面这个例子:
// Java语言
public static void main(String[] args) {
int i1 = 2147483647;
int i2 = 1;
System.out.printf("2147483647+1=%d\\n", i1+i2);
}
// 输出结果:
2147483647+1=-2147483648
两个正数 2147483647 和 1 相加,实际运行结果却是一个负数 -2147483648。原因是,运算结果超出了 int 类型的表示范围,我们把这种现象称作 溢出 。
接下来,我们将介绍整数类型常见的几种算术运算,包括当运算出现溢出时,计算机系统的处理方式。
加法
(1)无符号整数加法运算
对两个 w 位的无符号整数 ,有 ;如果仍用一个 w 位的整数表示相加结果,那么当结果在 范围时,也即结果需要 w + 1 位表示时,运算就产生溢出了。
如果出现溢出,系统会对结果进行截断,只保留低 w 位 。
比如,w = 4 场景下的一些例子:

因此,如果用 表示 w 位无符号整数的加法运算,那么它有如下规则:
其中,溢出场景因为对结果的进行截断,舍去了 位,所以结果需要减去 。
(2)有符号整数加法运算
对两个 w 位的有符号整数 ,有 ;如果仍用一个 w 位的整数表示相加结果,那么当结果在 和 范围时,运算就产生溢出了。
比如,w = 4 场景下的一些例子:

由上述例子可知, 两个 w 位的负数相加,即使结果需要 w + 1 位表示,也可能是正常场景。这取决于截断位 w 位后的最高位,为 1 则还属于正常场景,为 0 则属于溢出场景 。
因此,如果用 表示 w 位有符号整数的加法运算,那么它有如下规则:
- 正溢出场景下 ,原本 ,但按照补码编码方式,实际变成了 ,所以就有 。
- 负溢出场景下 ,w 位一定是 0,原本 ,结果截断之后,实际变成了 ,所以就有 。
为什么负溢出场景下,w 位一定是 0 ?
负溢出场景出现的条件是 ,也即 :
如果要使上述不等式成立, 必然为 0.
前面很多公式,但记住这个就行, 无符号整数和有符号整数的加法运算规则,本质都是一样的,可以拆解成 4 步 :
- 先计算出真实加法运算的结果值。
- 对结果值用 w + 1 位二进制表示。
- 再将 w + 1 位的二进制结果截断,保留低 w 位。
- 将截断后的 w 位二进制值转换回十进制整数,得到最终结果。无符号整数用无符号编码,有符号整数用补码编码。
取反
取反,也即求相反数,给定一个整数 ,那么它的相反数 ,也即满足 。
(1)无符号整数的取反
对一个 w 位的无符号整数 ,对它取反,也即找到一个整数 ,使得 :
- 当 ,那么很容易得出 ;
- 当 x > 0,只有在溢出场景才会存在 的可能。由前文可知,无符号整数加法溢出场景下, 时,有,。
因此,如果用 表示 w 位无符号整数的取反运算,那么它有如下规则:
比如,w = 8 场景下的例子:
// C++
int main() {
uint8_t i1 = 0;
uint8_t i2 = -i1;
printf("i1=%u\\n", i1);
printf("-i1=%u\\n", i2);
uint8_t i3 = 100;
uint8_t i4 = -i3;
printf("i3=%u\\n", i3);
printf("-i3=%u\\n", i4);
printf("2^8-i3=256-%u=%u\\n", i3, 256-i3);
return 0;
}
// 输出结果
i1=0
-i1=0
i3=100
-i3=156
2^8-i3=256-100=156
(2)有符号整数的取反
对一个 w 位的有符号整数 ,对它取反,也即找到一个整数 ,使得 :
- 当 ,很容易得出 ,因为此时 ,仍是有效的范围。
- 当 ,因为 已经不再有效范围内,所以只能是溢出场景。而 ,截断为 w 之后,刚好为 0。所以,此时 。
因此,如果用 表示 w 位有符号整数的取反运算,那么它有如下规则:
比如,w = 8 场景下的例子:
// C++
int main() {
int8_t i1 = -128;
int8_t i2 = -i1;
printf("i1=%d\\n", i1);
printf("-i1=%d\\n", i2);
int8_t i3 = 100;
int8_t i4 = -i3;
printf("i3=%d\\n", i3);
printf("-i3=%d\\n", i4);
return 0;
}
// 输出结果
i1=-128
-i1=-128
i3=100
-i3=-100
乘法
前面介绍加法时说过,无符号整数和有符号整数的加法运算都可以拆成 4 步,这对乘法运算也适用。
对于无符号整数 ,那么 ,即无符号整数的乘法运算结果最多需要 2w 位来表示。
比如,w = 8 时,无符号整数的例子:
// C++
int main() {
uint8_t i1 = 100;
uint8_t i2 = 2;
uint8_t i3 = i1 * i2;
printf("normal: i1 * i2 = %d * %d = %d\\n", i1, i2, i3);
uint8_t i4 = 100;
uint8_t i5 = 3;
uint8_t i6 = i4 * i5;
printf("overflow: i4 * i5 = %d * %d = %d\\n", i4, i5, i6);
return 0;
}
// 输出结果
normal: i1 * i2 = 100 * 2 = 200
overflow: i4 * i5 = 100 * 3 = 44
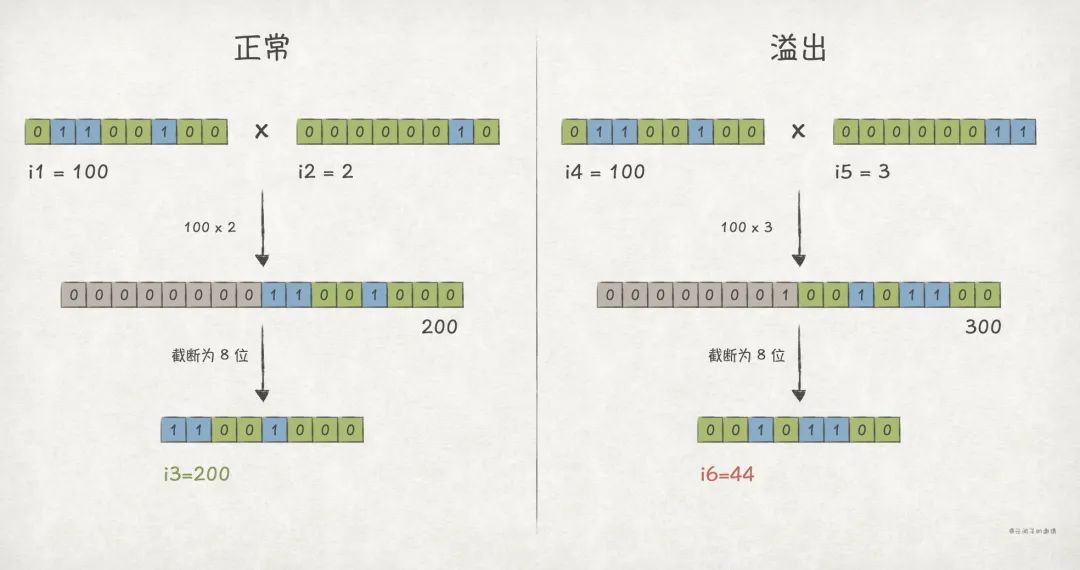
对于有符号整数 ,那么 ,即有符号整数的乘法运算结果最多也需要 2w 位来表示。
比如,w = 8 时,有符号整数的例子:
// C++
int main() {
int8_t i1 = -50;
int8_t i2 = 2;
int8_t i3 = i1 * i2;
printf("normal: i1 * i2 = %d * %d = %d\\n", i1, i2, i3);
int8_t i4 = -128;
int8_t i5 = 127;
int8_t i6 = i4 * i5;
printf("overflow: i4 * i5 = %d * %d = %d\\n", i4, i5, i6);
return 0;
}
// 输出结果
normal: i1 * i2 = -50 * 2 = -100
overflow: i4 * i5 = -128 * 127 = -128
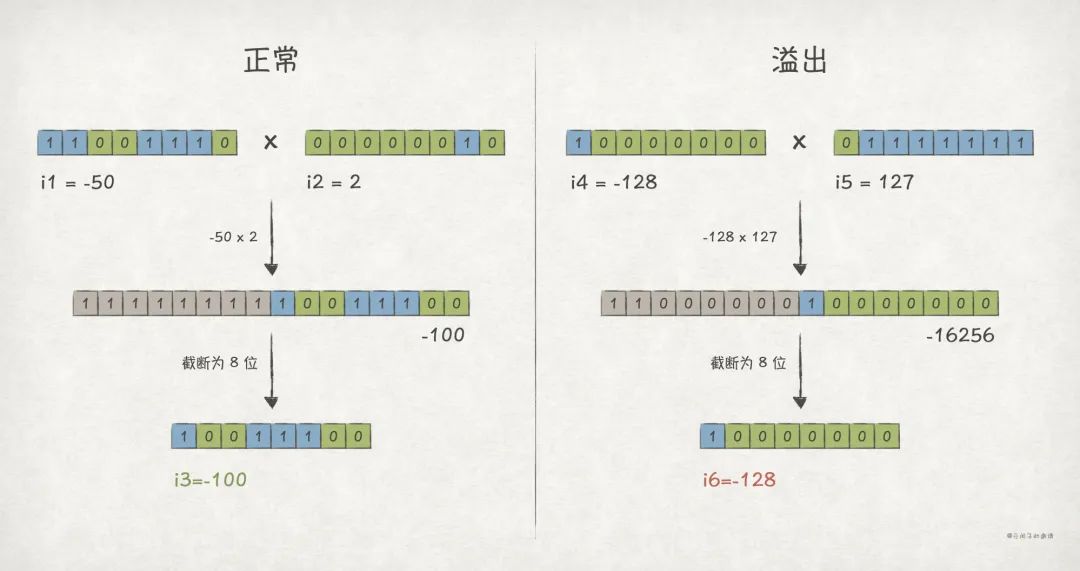
大部分机器上,乘法运算消耗 3 ~ 10 个 CPU 时钟周期,而加法运算和位运算只消耗 1 个时钟周期,所以,追求极致性能的程序都会想办法通过加法运算和位运算来替代乘法运算。
如果不考虑截断,对 左移 k 位,会得到:
也即,对 左移 k 位 相当于乘以 。
如果考虑截断,就会存在溢出场景,对于 w 位的整数,左移 k 位效果也等同于 或 。
比如,w = 8 时,无符号整数的例子:
// C++
int main() {
uint8_t i1 = 100;
uint8_t i2 = 4;
uint8_t i3 = i1 * i2;
printf("i1 * i2 = %d * %d = %d\\n", i1, i2, i3);
uint8_t k = 2;
uint8_t i4 = i1 << k;
printf("i1 << k = %d << %d = %d\\n", i1, k, i4);
return 0;
}
// 输出结果
i1 * i2 = 100 * 4 = 144
i1 << k = 100 << 2 = 144
有符号整数的例子:
// C++
int main() {
int8_t i1 = -50;
int8_t i2 = 4;
int8_t i3 = i1 * i2;
printf("i1 * i2 = %d * %d = %d\\n", i1, i2, i3);
int8_t k = 2;
int8_t i4 = i1 << k;
printf("i1 << k = %d << %d = %d\\n", i1, k, i4);
return 0;
}
// 输出结果
i1 * i2 = -50 * 4 = 56
i1 << k = -50 << 2 = 56
那么,对于与任意常数 K 的相乘,有没可能转换为移位操作 ?
任意常数 K,可以表示成 的形式,也即,由一系列连续的 0 和 连续的 1 组成,比如 14 可以表示成 。
假设只存在一个连续的 1 序列,从高到低, 位于 n 到 m 位,比如 14 中,n = 3,m = 1,那么:
比如, 就可以表示成 或者 :
// C++
int main() {
int8_t x = 5;
int8_t K = 14;
printf("x * 14 = %d\\n", x*K);
printf("(x<<3) + (x<<2) + (x<<1) = %d\\n", (x<<3)+(x<<2)+(x<<1));
printf("(x<<4) - (x<<1) = %d\\n", (x<<4)-(x<<1));
return 0;
}
// 输出结果
x * 14 = 70
(x<<3) + (x<<2) + (x<<1) = 70
(x<<4) - (x<<1) = 70
同理,当 K 的二进制表示,存在多个连续的 1 序列时,也成立。
除法
除法运算比乘法运算更慢,通常需要 30 个 CPU 时钟以上 。同理, 也可以转换成右移运算,注意结果的取整:
// C++
int main() {
int8_t x = -50;
int8_t K = 4;
printf("x / 4 = %d\\n", x/K);
printf("x >> 2 = %d\\n", x>>2);
printf("(x+(1<<2))>>2 = %d\\n", (x+(1<<2))>>2);
uint8_t y = 50;
uint8_t Z = 4;
printf("y / 4 = %d\\n", y/Z);
printf("y >>> 2 = %d\\n", y>>2);
printf("(y+(1<<2))>>>2 = %d\\n", (y+(1<<2))>>2);
return 0;
}
// 输出结果
x / 4 = -12
x >> 2 = -13
(x+(1<<2))>>2 = -12
y / 4 = 12
y >>> 2 = 12
(y+(1<<2))>>>2 = 13
-
计算机
+关注
关注
19文章
7500浏览量
88022 -
编程
+关注
关注
88文章
3616浏览量
93761 -
编码
+关注
关注
6文章
944浏览量
54843 -
数值
+关注
关注
0文章
80浏览量
14372
发布评论请先 登录
相关推荐
简单介绍微型计算机的组成
深入理解计算机系统的数值类型
计算机系统对数值类型的编码、运算、转换原理介绍1
计算机系统对数值类型的编码、运算、转换原理介绍3
计算机系统对数值类型的编码、运算、转换原理介绍4





 计算机系统对数值类型的编码、运算、转换原理介绍2
计算机系统对数值类型的编码、运算、转换原理介绍2










评论