计算机系统对数值类型的编码、运算、转换原理介绍4
数值类型转换
数值类型间的转换，可以分成 2 类： 宽转换 （Widening Conversion）和 窄转换 （Narrowing Conversion）。
宽转换指往表示范围更广的类型转换，比如从 int 到 long、从 long 到 float；窄转换则相反。
整型间转换
（1）宽转换
整型间的宽转换不会产生溢出，无符号整数场景，高位补零；有符号整数场景，高位补符号位。
// C++
int main() {
int8_t i1 = 100;
cout << "int8_t i1: " << bitset<8>(i1) << endl;
cout << "int16_t i1: " << bitset<16>((int16_t) i1) << endl;
int8_t i2 = -100;
cout << "int8_t i2: " << bitset<8>(i2) << endl;
cout << "int16_t i2: " << bitset<16>((int16_t) i2) << endl;
uint8_t i3 = 200;
cout << "uint8_t i3: " << bitset<8>(i3) << endl;
cout << "uint16_t i3: " << bitset<16>((uint16_t) i3) << endl;
return 0;
}
// 输出结果
int8_t i1: 01100100
int16_t i1: 0000000001100100
int8_t i2: 10011100
int16_t i2: 1111111110011100
uint8_t i3: 11001000
uint16_t i3: 0000000011001000
（2）窄转换
整型间的窄转换直接进行高位截断，只保留低 n 位。比如 16 位的 int16 转换为 8 位的 int8，直接保留 int16 类型值的低 8 位作为转换结果。
// C++
int main() {
int16_t i1 = 200;
cout << "int16_t i1: " << bitset<16>(i1) << endl;
cout << "int8_t i1: " << bitset<8>((int8_t) i1) << endl;
int16_t i2 = -200;
cout << "int16_t i2: " << bitset<16>(i2) << endl;
cout << "int8_t i2: " << bitset<8>((int8_t) i2) << endl;
uint16_t i3 = 300;
cout << "uint16_t i3: " << bitset<16>(i3) << endl;
cout << "uint8_t i3: " << bitset<8>((uint8_t) i3) << endl;
return 0;
}
// 输出结果
int16_t i1: 0000000011001000
int8_t i1: 11001000
int16_t i2: 1111111100111000
int8_t i2: 00111000
uint16_t i3: 0000000100101100
uint8_t i3: 00101100
（3）无符号整数与有符号整数间的转换
无符号整数与有符号整数间的转换规则是：
- 如果两者二进制位数一致，比如
int8到uint8的转换，则二进制数值不变，只是改变编码方式； - 如果位数不一致，比如
int16到uint8的转换，则二进制数值，先按照宽转换或窄转换规则转换，再改变编码方式。
// C++
int main() {
uint8_t i1 = 200;
cout << "uint8_t i1, decimal: " << +i1 << ", binary: " << bitset<8>(i1) << endl;
cout << "int8_t i1, decimal: " << +(int8_t) i1 << ", binary: " << bitset<8>((int8_t) i1) << endl;
int16_t i2 = -300;
cout << "int16_t i2, decimal: " << +i2 << ", binary: " << bitset<16>(i2) << endl;
cout << "uint8_t i2, decimal: " << +(uint8_t) i2 << ", binary: " << bitset<8>((uint8_t) i2) << endl;
return 0;
}
// 输出结果
uint8_t i1, decimal: 200, binary: 11001000
int8_t i1, decimal: -56, binary: 11001000
int16_t i2, decimal: -300, binary: 1111111011010100
uint8_t i2, decimal: 212, binary: 11010100
整数与浮点数间转型
（1）宽转换
整型到浮点数类型的转换这一方向，为宽转换：
- 如果浮点数的精度，能够表示整数，则正常转换。
- 如果浮点数精度，无法表示整数，则需要近似，会导致精度丢失。
// Java
public static void main(String[] args) {
int i1 = 1234567;
System.out.printf("int i1: %d, float i1: ", i1);
System.out.println((float) i1);
int i2 = 123456789;
System.out.printf("int i2: %d, float i2: ", i2);
System.out.println((float) i2);
}
// 输出结果
int i1: 1234567, float i1: 1234567.0
int i2: 123456789, float i2: 1.23456792E8
上述例子中，i2=123456789 超过 float 类型能够表示的精度，所以为近似后的结果 1.23456792E8。
那么，为什么 123456789 会近似为 1.23456792E8？
要解释该问题，首先要把它们转换成二进制表示：
public static void main(String[] args) {
...
System.out.println("int i2: " + int2BinaryStr(i2));
System.out.println("float i2: " + float2BinaryStr((float) i2));
}
// 输出结果
int i2: 00000111010110111100110100010101
float i2: 01001100111010110111100110100011
接下来，我们根据 IEEE 浮点数的编码规则，尝试将 int i2 转换成 float i2：
int i2的二进制 ，可以写成 ，对应到 的形式，可以确认 s = 0，E = 26，M = 1.11010110111100110100010101。- float 类型中 k = 8，有，，得出 e = 153，按 k 位无符号编码表示为 。
- 同理，由 ，但由于 float 类型的 n = 23，而 m 一共有 26 位，因此需要按照 round-to-even 规则，对 0.11010110111100110100010101进行近似，保留 23 位小数，得到 0.11010110111100110100011，所以 m 为
- 最后，将 s、e、m 按照 float 单精度的编码格式组合起来，就是 ，转换成十进制，就是
1.23456792E8。
（2）窄转换
浮点数类型到整型的转换这一方向，为窄转换：
- 如果浮点数的整数部分，能够用整型表示，则直接舍去小数，保留整数部分。
- 如果超出了整型范围，则结果为该整型的最大/最小值。
// Java
public static void main(String[] args) {
float f1 = 12345.123F;
System.out.print("float f1: ");
System.out.print(f1);
System.out.printf(", int f1: %d\\n", (int) f1);
float f2 = 1.2345E20F;
System.out.print("float f2: ");
System.out.print(f2);
System.out.printf(", int f2: %d\\n", (int) f2);
float f3 = -1.2345E20F;
System.out.print("float f3: ");
System.out.print(f3);
System.out.printf(", int f3: %d\\n", (int) f3);
}
// 输出结果
float f1: 12345.123, int f1: 12345
float f2: 1.2345E20, int f2: 2147483647
float f3: -1.2345E20, int f3: -2147483648
浮点数间转型
（1）宽转换
单精度 float 到 双精度 double 为宽转换，不会出现精度丢失的问题。
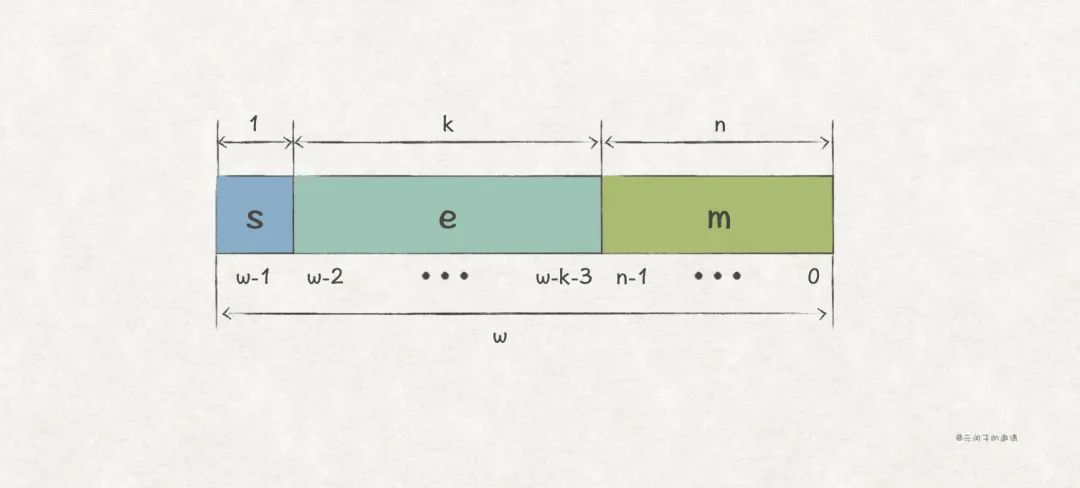
对于 ，规则如下：
- s 保持不变。
- 在 E 保持不变的前提下，因为
float的 k = 8，而double的 k = 11，所以两者的 e 会有所不同。 - 在 M 保持不变的前提下，
float的 n = 23，而double的 n =52，所以 m 需要低位补 52 - 23 = 29 个 0。
// Java
public static void main(String[] args) {
float f1 = 1.2345E20F;
System.out.print("float f1: ");
System.out.print(f1);
System.out.print(", double f1: ");
System.out.println((double) f1);
System.out.println("float f1: " + float2BinaryStr(f1));
System.out.println("double f1: " + double2BinaryStr((double) f1));
}
// 输出结果
float f1: 1.2345E20, double f1: 1.2344999897320129E20
float f1: 01100000110101100010011011010000
double f1: 0100010000011010110001001101101000000000000000000000000000000000
（2）窄转换
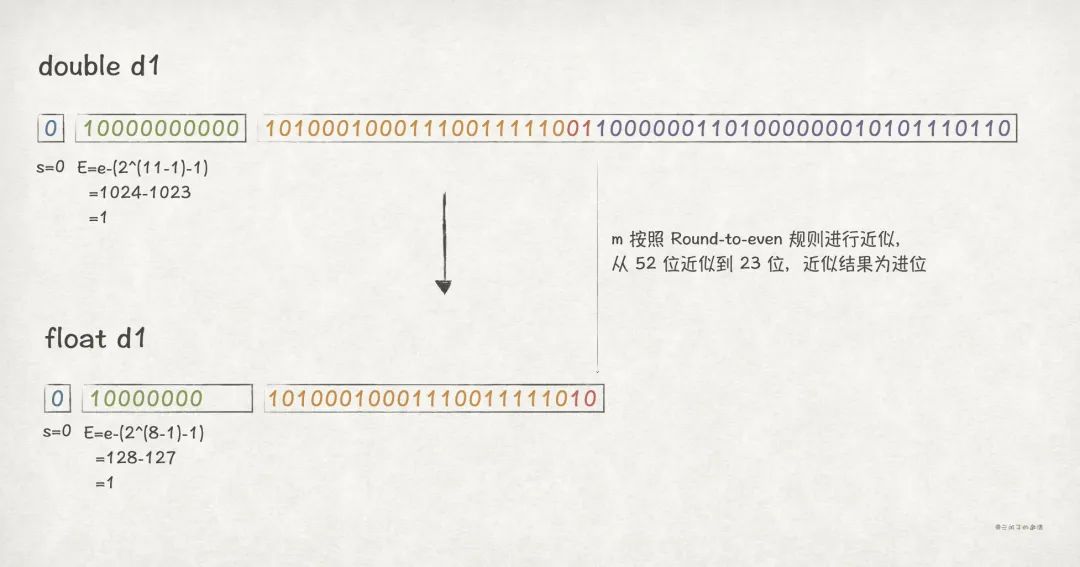
double 到 float 为窄转换，会存在精度丢失问题。
如果 double 值超出了 float 的表示范围，则转换结果为 Infinity：
// Java
public static void main(String[] args) {
double d1 = 1E200;
System.out.print("double d1: ");
System.out.println(d1);
System.out.print("float d1: ");
System.out.println((float) d1);
double d2 = -1E200;
System.out.print("double d2: ");
System.out.println(d2);
System.out.print("float d2: ");
System.out.println((float) d2);
}
// 输出结果
double d1: 1.0E200
float d1: Infinity
double d2: -1.0E200
float d2: -Infinity
如果 double 值还在 float 的表示范围内，则按照如下转换规则：
- s 保持不变。
- 在 E 保持不变的前提下，因为
float的 k = 8，而double的 k = 11，所以两者的 e 会有所不同。 - 对于 M，因为
float的 n = 23，而double的 n = 52，所以转换到 float 之后，需要进行截断，只保留高 23 位。
// Java
public static void main(String[] args) {
double d1 = 3.267393471324506;
System.out.print("double d1: ");
System.out.println(d1);
System.out.print("float d1: ");
System.out.println((float) d1);
System.out.println("double d1: " + double2BinaryStr(d1));
System.out.println("float d1: " + float2BinaryStr((float) d1));
}
// 输出结果
double d1: 3.267393471324506
float d1: 3.2673936
double d1: 0100000000001010001000111001111100110000001101000000010101110110
float d1: 01000000010100010001110011111010
最后
本文花了很长的篇幅，深入介绍了计算机系统对数值类型的编码、运算、转换的底层原理。
数值类型间的转换是最容易出现隐藏 bug 的地方 ，特别是无符号整数与有符号整数之间的转换。所以，很多现代的编程语言，如 Java、Go 等都不再支持无符号整数，根除了该隐患。
另外，浮点数的编码方式，注定它只能精确表示一小部分的数值范围，大部分都是近似，所以才有了不能用等号来比较两个浮点数的说法。
数值类型虽然很基础，但使用时一定要多加小心。希望本文能够加深你对数值类型的理解，让你写出更健壮的程序。
声明：本文内容及配图由入驻作者撰写或者入驻合作网站授权转载。文章观点仅代表作者本人，不代表电子发烧友网立场。文章及其配图仅供工程师学习之用，如有内容侵权或者其他违规问题，请联系本站处理。
举报投诉
-
二进制
+关注
关注
2文章
792浏览量
41591 -
计算机
+关注
关注
19文章
7404浏览量
87688 -
编程
+关注
关注
88文章
3586浏览量
93576
发布评论请先 登录
相关推荐
简单介绍微型计算机的组成
你了解自己的计算机？或者知道单片机的组成吗？这一小节主要简单介绍微型计算机的组成，以及微型计算机系统经常用到的概念，包括组成、工作过程、工作原理、数
发表于 01-10 07:11
深入理解计算机系统的数值类型
在计算机系统中，整数可以分成 无符号（unsigned）整数 和 有符号（signed）整数 两大类，这之下，按照类型表示的 bit 位大小，又可细分成 8 位的 char/byte/int8
计算机系统对数值类型的编码、运算、转换原理介绍1
。正因太熟悉，我们往往不会深究它们的底层原理。因为平时的工作中，知道个大概，也够用了。
但，在某些业务场景下，比如金融业务，数值运算不准确会带来灾难性的后果。这时，你就必须清楚数值类型
计算机系统对数值类型的编码、运算、转换原理介绍2
。正因太熟悉，我们往往不会深究它们的底层原理。因为平时的工作中，知道个大概，也够用了。
但，在某些业务场景下，比如金融业务，数值运算不准确会带来灾难性的后果。这时，你就必须清楚数值类型
计算机系统对数值类型的编码、运算、转换原理介绍3
。正因太熟悉，我们往往不会深究它们的底层原理。因为平时的工作中，知道个大概，也够用了。
但，在某些业务场景下，比如金融业务，数值运算不准确会带来灾难性的后果。这时，你就必须清楚数值类型
计算机系统中的关键组件有哪些
在计算机系统中，关键组件的协同工作构成了其强大的数据处理和运算能力。这些组件不仅决定了计算机的性能，还影响着用户的使用体验。以下是对计算机系统中关键组件的详细阐述，包括它们的定义、功能
微处理器如何控制计算机系统
微处理器，作为计算机系统的核心部件，承担着控制整个计算机系统运行的重要任务。它不仅是计算机的运算中心，还是控制中心，负责执行程序指令、处理数据以及协调
工商网监
评论