支持向量机寻找最优分类超平面的优化问题

根据，在线性可分情况下，支持向量机寻找最优分类超平面的优化问题可以表示为：

最小化：1/2||ω||2，

限制条件：yi(ωTXi+b)≥1，i=1~N。

求解上述最优化问题，可得出一组ω和b的值，使得ωTx+b=0所表示的超平面为最优分类超平面。

但在训练样本是线性不可分的情况下，上述最优化问题不存在合适的解（个人理解：不存在合适的解的原因是上述最优化问题的本质是求解最优分类超平面，最优分类超平面应满足可将训练数据完全分为两类的条件，但在训练样本是线性不可分的情况，不存在满足上述条件的超平面）。

因此，寻找线性不可分的训练样本的最优超平面时，需将上述优化问题的限制条件放松。放松限制条件的方式是引入松弛变量δi（slack variable），将上述优化问题的限制条件改写为：

yi(ωTXi+b)≥1-δi，i=1~N

在线性不可分的情况下，训练样本的数据无法满足均yi(ωTXi+b)≥1，但可通过调整δi的值使所有训练数据均满足yi(ωTXi+b)≥1-δi。同时，为使分类的准确性尽可能高，δi的值也需被限定。

根据上述思路，在线性不可分的情况下，支持向量机寻找最优分类超平面的优化问题可以表示为：

最小化：1/2||ω||2+C∑δi或1/2||ω||2+C∑δi2，

限制条件：（1）δi≥0，i=1~N；（2）yi(ωTXi+b)≥1-δi，i=1~N。

其中，最小化1/2||ω||2+C∑δi或1/2||ω||2+C∑δi2使δi的取值尽可能小，C为比例因子，C的值需人为设定。算法中需人为设定的参数被称为算法的超参数（hyper parameter）。

在实际应用中，开发人员会不断被变化超参数值，并测试各种超参数算法的识别率，以选取使算法识别率达至最高的超参数值。

如果一个算法的超参数越多，该算法需手动调整的部分越多，其自动性越低，支持向量机是超参数较少的算法模型，超参数较多的算法模型包括：人工神经网络、卷积神经网络（根据百度百科：卷积神经网络是深度学习的代表算法之一）等。

尽管在线性不可分的情况下，机器学习可以通过使1/2||ω||2+C∑δi或1/2||ω||2+C∑δi2最小化寻找最优分类超平面，但该方法的分类准确率不一定较高。

如图一所示，图一中的直线为机器学习通过支持向量机寻找最优分类超平面，但该直线对图一中圆圈和叉的分类的准确率与随机猜测的准确率差异不大。

 

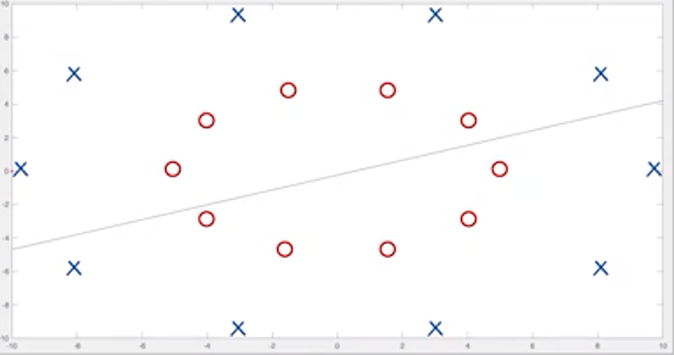
图一，图片来源：中国慕课大学《机器学习概论》

此情况出现的原因是通过使1/2||ω||2+C∑δi或1/2||ω||2+C∑δi2最小化寻找最优分类超平面的算法模型是线性的，即假设算法模型的分类函数是线性的。因此，该算法模型对分类函数为非线性函数的训练样本进行分类时，将出现分类错误的情况。

当训练样本的非线性分类函数与线性函数差异较大时，分类错误的情况出现的概率将较大，可能出现分类的准确率与随机猜测的准确率差异不大的情况。

审核编辑：刘清