本文主要来源于中国慕课大学《机器学习概论》学习笔记
根据机器学习相关介绍(9)——支持向量机(线性不可分情况),通过引入松弛变量δi将支持向量机推广至解决非线性可分训练样本分类的方式不能解决所有非线性可分训练样本的分类问题。因此,支持向量机的可选函数范围需被扩展以提升其解决非线性可分训练样本分类问题的能力。
支持向量机可选函数范围被扩大的方式与其他机器学习算法可选函数范围的被扩大方式不同。
其他算法(包括:人工神经网络、决策树等)可选函数范围被扩大的方式是直接产生更多可选函数。例如:人工神经网络可通过多层非线性函数的组合产生类似椭圆的曲线,以解决类似图一的分类问题。
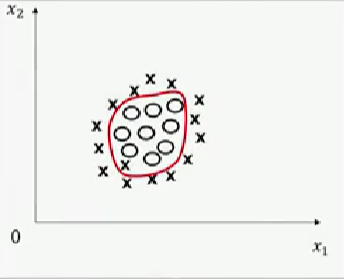
图一,图片来源:中国慕课大学《机器学习概论》
支持向量机则通过将特征空间由低维映射至高维,并在高维度中采用线性超平面分类数据。下文通过案例介绍该数据分类方式。
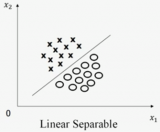
如图二所示,圆圈和叉对应的向量分别为X1=[0,0]T(左下叉),X2=[1,1]T(右上叉),X3=[1,0]T(右下圆圈),X4=[0,1]T(左上圆圈),即X1、X2属于同一类别,X3、X4属于同一类别。图二所示分类问题为线性不可分分类问题,机器学习算法或人类均不能找到一条直线将圆圈和叉完全分类。
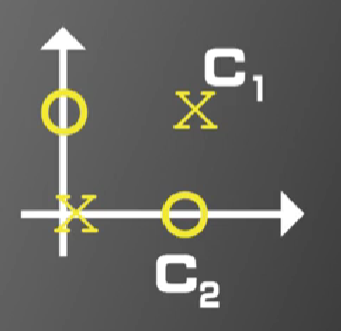
图二,图片来源:中国慕课大学《机器学习概论》
但若构造一个二维特征空间到五维特征空间的映射φ(x),该案例可能转化为线性可分分类问题。
二维特征空间到五维特征空间映射的一种方式如下:
当在二维特征空间向量x=[a,b]T时,其五维特征空间向量φ(x)=[a2,b2,a,b,ab]T。
根据此映射方式,二维特征空间向量X1、X2、X3、X4对应的五维特征空间向量分别为φ(X1)=[0,0,0,0,0]T,φ(X2)=[1,1,1,1,1]T,φ(X3)=[1,0,1,0,0]T,φ(X4)=[0,1,0,1,0]T。
设:ω=[-1,-1,-1,-1,6]T,b=1,则:ωTφ(X1)+b=1>0,ωTφ(X2)+b=3>0,ωTφ(X3)+b=-1<0,ωTφ(X4)+b=-1<0,根据线性可分的定义,此时ωTφ(X1)+b=0所代表的函数在五维特征空间中将圆圈和叉完全分类。
支持向量机通过将特征空间由低维映射至高维解决非线性分类问题的方式可基于以下定理理解:
在一个M维空间上随机取N个训练样本,随机对每个训练样本赋予标签+1或-1,同时假设这些训练样本线性可分的概率为P(M),当M趋于无穷大时,P(M)=1。
即增加特征空间维度M时,带估计参数ω和b的维度也会增加,算法模型的自由度增加。因此,算法模型更可能将低维时无法完全分类的问题在高维完全分类。
综上,支持向量机的优化问题可改写为:
最小化:1/2||ω||2+C∑δi或1/2||ω||2+C∑δi2,
限制条件:(1)δi≥0,i=1~N;(2)yi(ωTφ(Xi)+b)≥1-δi,i=1~N。
其中,ω的维度与φ(Xi)的维度相同。
审核编辑:汤梓红
-
神经网络
+关注
关注
42文章
4785浏览量
101289 -
函数
+关注
关注
3文章
4350浏览量
63076 -
机器学习
+关注
关注
66文章
8455浏览量
133186
原文标题:机器学习相关介绍(10)——支持向量机(低维到高维的映射)
文章出处:【微信号:行业学习与研究,微信公众号:行业学习与研究】欢迎添加关注!文章转载请注明出处。
发布评论请先 登录
相关推荐



支持向量机——机器学习中的杀手级武器!
基于向量机随机投影特征降维分类下降解决方案




 机器学习相关介绍:支持向量机(低维到高维的映射)
机器学习相关介绍:支持向量机(低维到高维的映射)
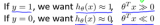
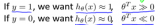
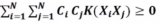










评论