奈奎斯特-香农定理：了解采样系统

奈奎斯特采样定理，或更准确地说是奈奎斯特-香农定理，是支配混合信号电子系统设计的基本理论原则。

如果没有模数转换和数模转换，就不会存在我们所知道的现代技术。事实上，这些操作已经变得如此普遍，以至于说模拟信号可以转换为数字信号再转换回模拟信号而不会丢失任何重大信息，这听起来像是不言而喻。

但是我们怎么知道确实是这样呢？为什么采样是一种非破坏性操作，当它似乎丢弃了我们在各个样本之间观察到的如此多的信号行为时？

我们究竟如何从一个看起来像这样的信号开始：

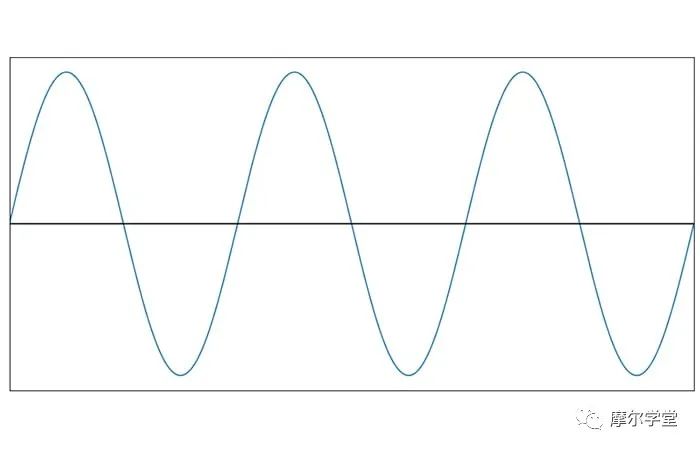
并将其数字化为：

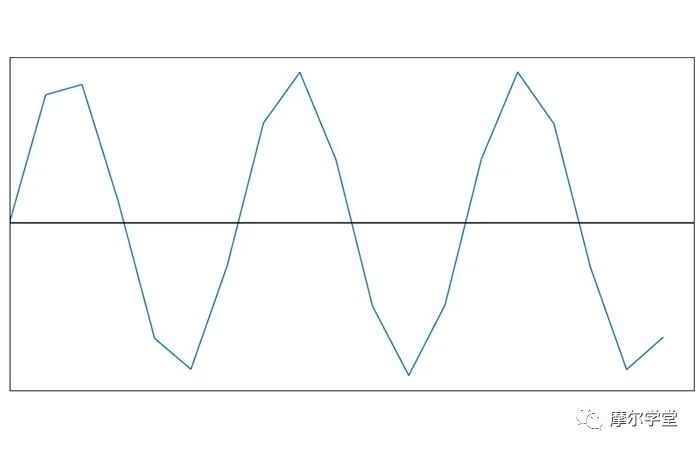
然后还敢声称可以在不丢失信息的情况下恢复原始信号？

奈奎斯特-香农定理

这样的说法是可能的，因为它符合现代电气工程最重要的原则之一：

如果系统以超过信号最高频率至少两倍的速率对模拟信号进行均匀采样，则可以从采样产生的离散值中完美地恢复原始模拟信号。

关于这个定理还有很多要说的，但首先，让我们试着弄清楚如何称呼它。

香农？奈奎斯特？科捷利尼科夫？惠特克？

我当然不是决定谁应该因制定、证明或解释香农-奈奎斯特-科特尼科夫-惠特克采样和插值理论而获得最多荣誉的人。所有这四个人都有某种显着的参与。

然而，Harry Nyquist 的角色似乎已经超出了其原有的意义。例如，在Tan 和 Jiang 的Digital Signal Processing: Fundamentals and Applications中，上述原理被确定为“Shannon sampling theorem”，在Sedra 和 Smith 的Microelectronic Circuits中，我发现以下句子：“The fact that we可以对有限数量的样本进行处理……而忽略样本之间的模拟信号细节是基于……香农的采样定理。”

因此，我们可能应该避免使用“奈奎斯特采样定理”或“奈奎斯特采样理论”。如果我们需要将一个名称与这个概念相关联，我建议我们只包括 Shannon 或包括 Nyquist 和 Shannon。事实上，也许是时候过渡到更匿名的东西了，比如“基本采样定理”。

如果您觉得这有点迷惑，请记住，上述采样定理与奈奎斯特速率不同，后者将在本文后面进行解释。我认为没有人试图将奈奎斯特与其速率分开，所以我们最终得到了一个很好的折衷方案：香农得到定理，奈奎斯特得到速率。

时域采样理论

如果我们将采样定理应用于频率为 f SIGNAL的正弦波，如果我们想要实现完美重建，就必须在 f SAMPLE ≥ 2f SIGNAL处对波形进行采样。换句话说，我们每个正弦周期至少需要两个样本。让我们首先尝试通过在时域中思考来理解这个要求。

在下图中，正弦波的采样频率远高于信号频率。

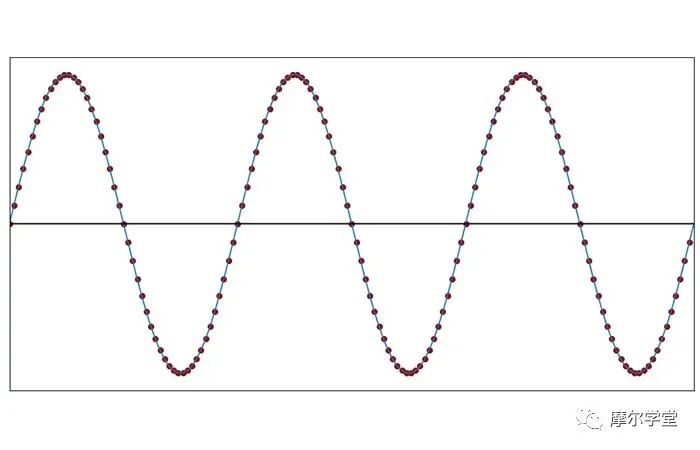
每个圆圈代表一个采样时刻，即测量模拟电压并将其转换为数字的精确时刻。

为了更好地可视化此采样过程为我们提供的内容，我们可以绘制样本值，然后用直线将它们连接起来。下图中显示的直线近似看起来与原始信号完全一样：采样频率相对于信号频率非常高，因此线段与相应的曲线正弦曲线段没有明显不同。

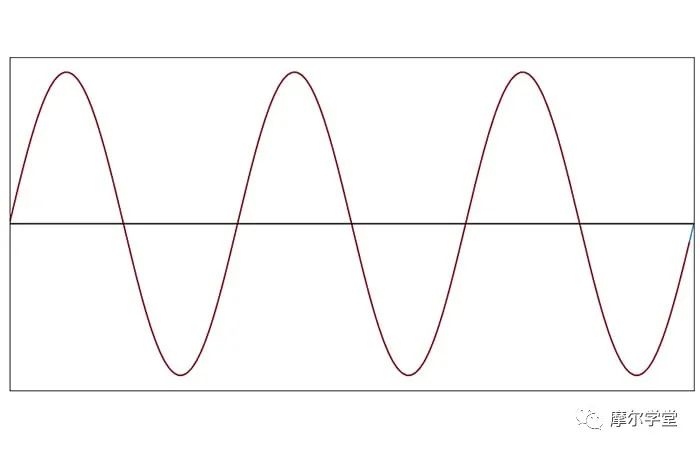
当我们降低采样频率时，直线近似的外观与原来的不同。

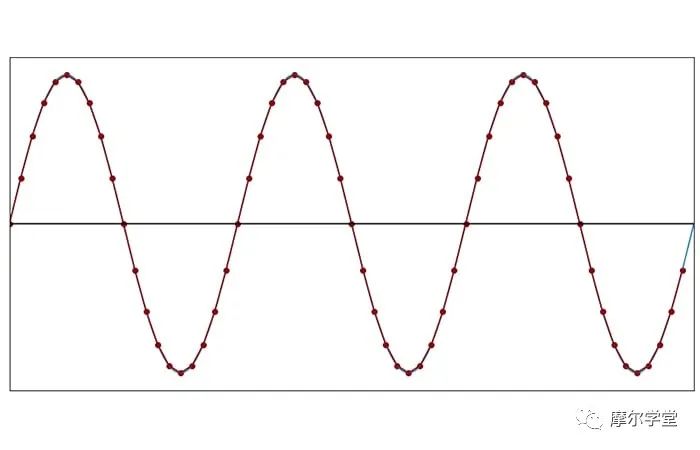
每个周期 20 个样本（f样本= 20f信号）

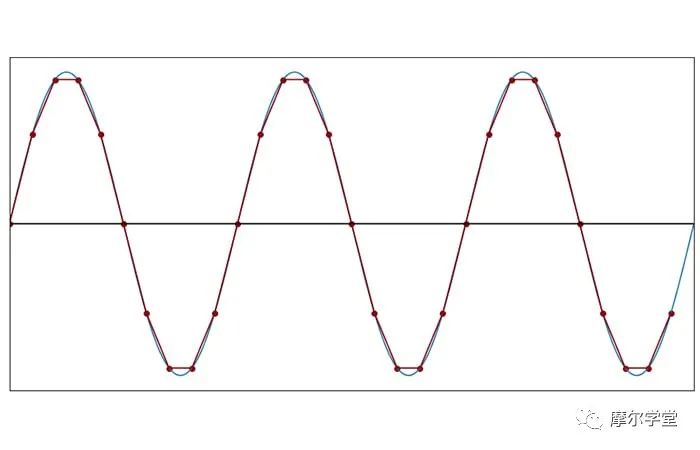
每个周期 10 个样本（f样本= 10f信号）

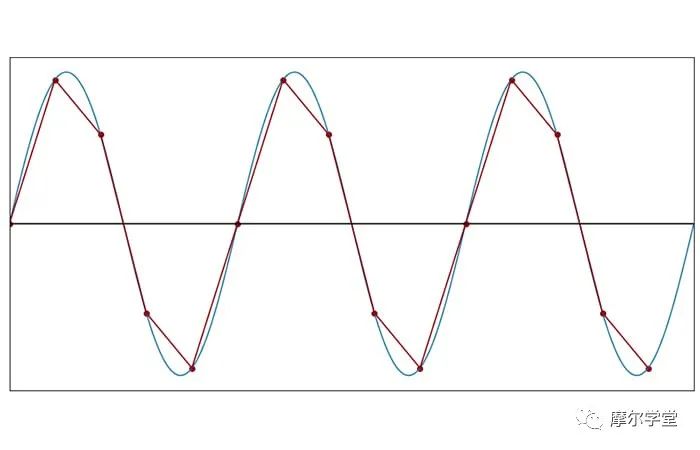
每个周期 5 个样本（f样本= 5f信号）

在 fSAMPLE= 5fSIGNAL时，离散时间波形不再是连续时间波形的令人满意的表示。但是请注意，我们仍然可以清楚地识别离散时间波形的频率。信号的循环性质并没有丢失。

阈值：每个周期两个样本

当我们将每个周期的样本数减少到五个以下时，采样产生的数据点将继续保留模拟信号的循环性质。然而，最终我们达到了频率信息被破坏的程度。考虑以下情节：

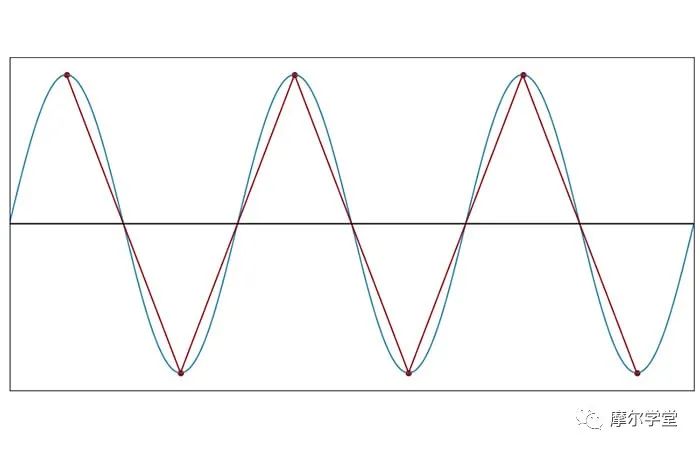
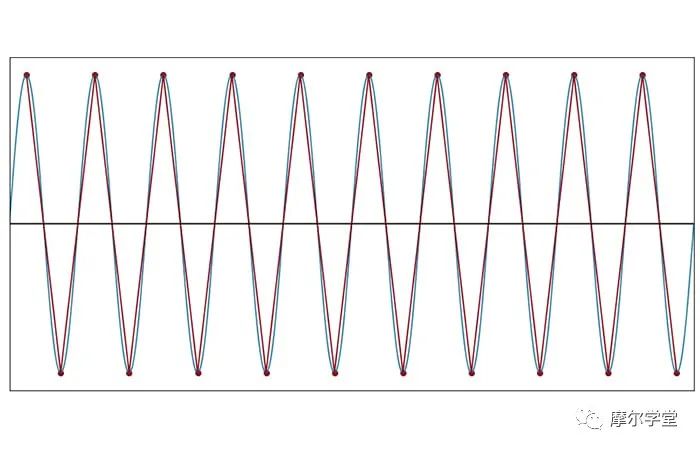
每个周期 2 个样本（f样本= 2f信号）

当 fSAMPLE= 2fSIGNAL时，正弦曲线形状完全消失。尽管如此，采样数据点产生的三角波并没有改变正弦波的基本周期性。三角波的频率与原始信号的频率相同。

但是，一旦我们将采样频率降低到每个周期少于两个样本的程度，就无法再做出这种说法。因此，对于原始波形中的最高频率，每个周期两个样本是混合信号系统中至关重要的阈值，相应的采样频率称为奈奎斯特速率：

如果我们以低于奈奎斯特速率的频率对模拟信号进行采样，我们将无法完美地重建原始信号。

接下来的两个图展示了当采样频率降至奈奎斯特速率以下时发生的循环等效性损失。

每个周期 2 个样本（f样本= 2f信号）

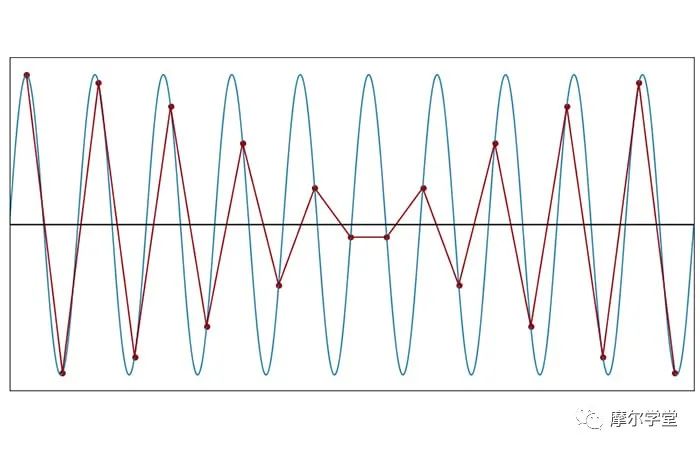
每个周期 1.9 个样本（f样本= 1.9f信号）

在 fSAMPLE= 1.9fSIGNAL时，离散时间波形从根本上获得了新的循环行为。采样模式的完全重复需要一个以上的正弦周期。

然而，当我们每个周期有 1.9 个样本时，采样频率不足的影响有点难以解释。接下来的情节使情况更加明朗。

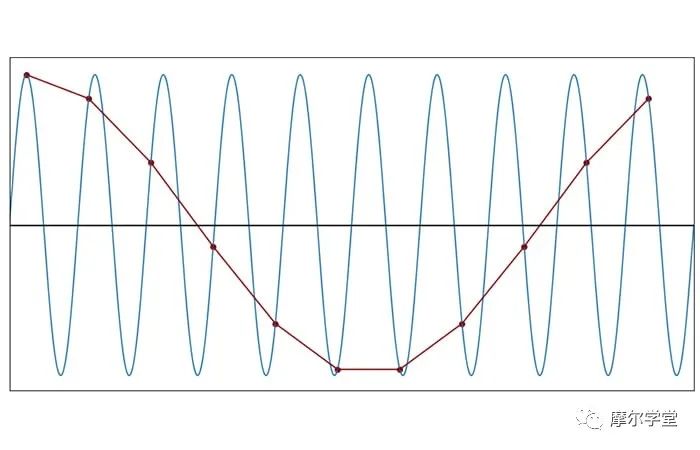
每个周期 1.1 个样本（f样本= 1.1f信号）

如果您对正弦曲线一无所知并使用以 1.1f SIGNAL采样产生的离散时间波形进行分析，您将对原始信号的频率形成严重错误的想法。此外，如果您拥有的只是离散数据，则不可能知道频率特性已被破坏。采样创建了原始信号中不存在的新频率，但您不知道该频率不存在。

底线是：当我们以低于奈奎斯特速率的频率进行采样时，信息将永久丢失，并且无法完美地重建原始信号。

结论

我们已经介绍了香农采样定理和奈奎斯特速率，并且我们试图通过观察时域中采样的影响来深入了解这些概念。




审核编辑：刘清