3D渲染——光栅化渲染原理解析

前言

随着技术的发展，基于 GPU 的渲染技术得到了广泛应用，日常生活中常见的 3D 动画和游戏都是通过计算机渲染技术来实现。当前主要的 3D 渲染模型包括光栅化渲染和光线追踪两大类，本文主要围绕光栅化渲染进行介绍，描述了简单场景下3D渲染过程，主要帮助读者了解基于光栅化的 3D 渲染原理及过程。本文为系列文章，并在下一篇系列文章中以 Intel Gen12 为例，讲述 GPU 一些基本硬件单元及如何利用硬件加速渲染过程。希望通过这种软件计算 + 硬件实现的方式，让大家了解 GPU 3D 渲染原理及过程。

在开始正式的介绍前，有以下几点说明：

在渲染过程中，涉及到向量、矩阵等数学知识不再阐述。在后面用到的时候会有提及。

文中选择了一个简单的模型场景，过程也尽可能简化。旨在重点讲述光栅化流程，便于读者理解。

推荐课程 GAMES101，文章后面用到的一些图片出自该课件。

光栅化过程

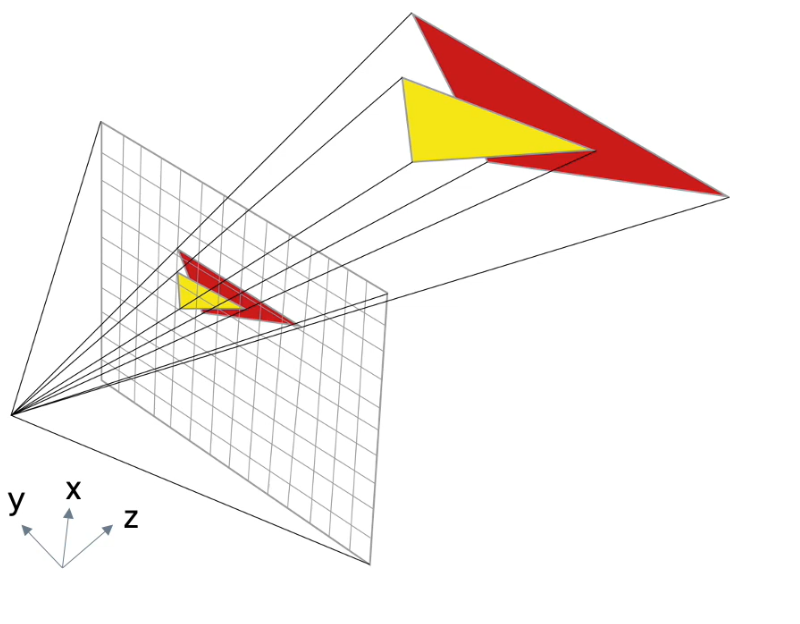
图0 光栅化示意图

图0 是光栅化的一个简易图，其中光栅化主要完成以下两个功能：

将几何图元（三角形/多边形）投影到屏幕上

将投影之后的图元分解成片段

模型建立

下文开始举例说明光栅化过程，为了更简单的说明光栅化，我们选用相对简单的模型，在三维空间中存在两个三角形，其中三角形1 三个顶点坐标分别为(-2, 0, -2)、(2, 0, -2)、(0, 2, -2)，三角形2 三个顶点坐标分别为(-1, 0.5, -20)、(2.5, 1, -20)、(3, -1.5, -20)，之所以后面三角形 z 绝对值比较大，是为了后面观察透视投影近大远小的效果。在模型中，除了被观察物体，还需要确认观察点的位置，这里将相机放在位置(0, 0, 0)，观察方向是 z 轴负方向（z-），向上向量为 y 轴正向（y+)。模型如图1所示：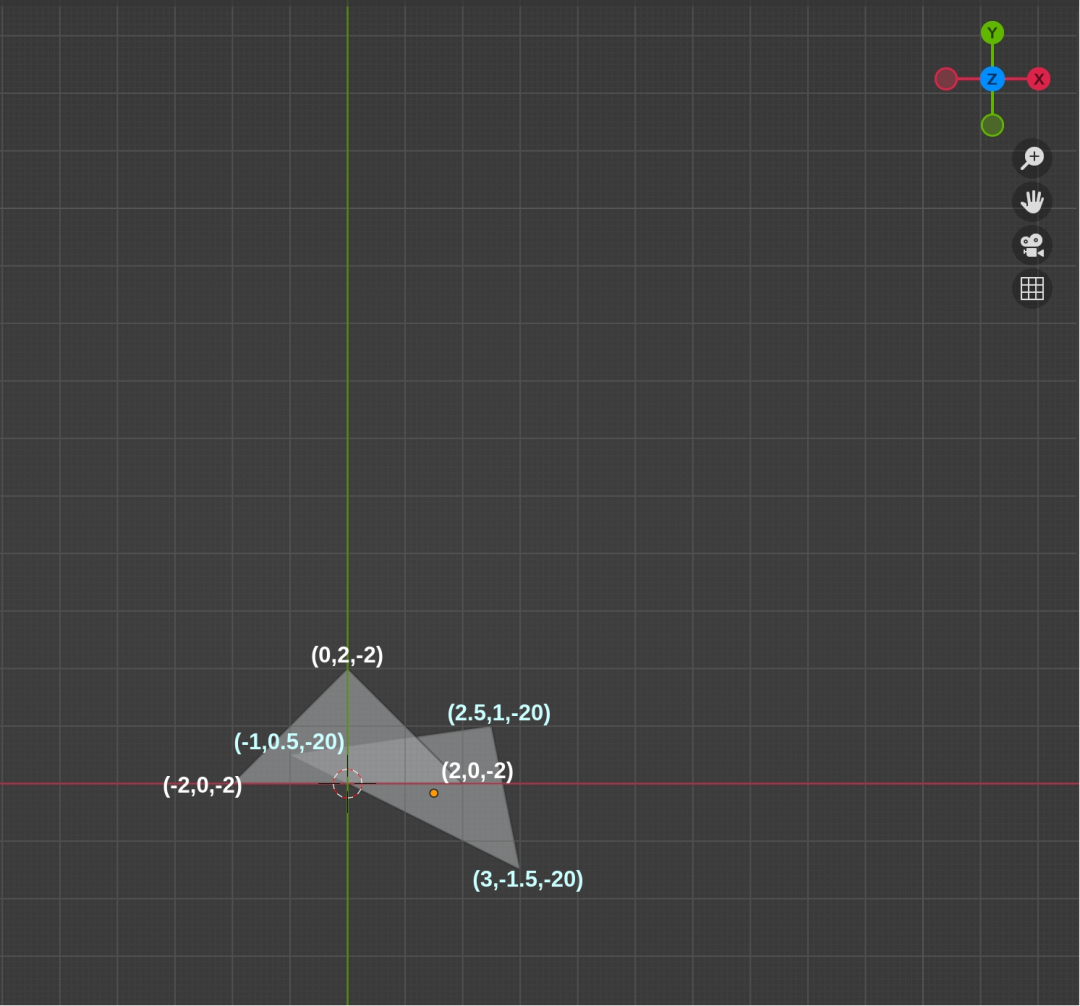



图1 模型顶视图

物体和相机的位置已经放好了，那么我们接下来要做的就是要将相机实际看到的内容最终显示到屏幕上。模型是三维的，而最终的成像是二维，所以这其中必然要有投影操作。

正交投影和透视投影

先来看一下透视投影和正交投影的效果图：

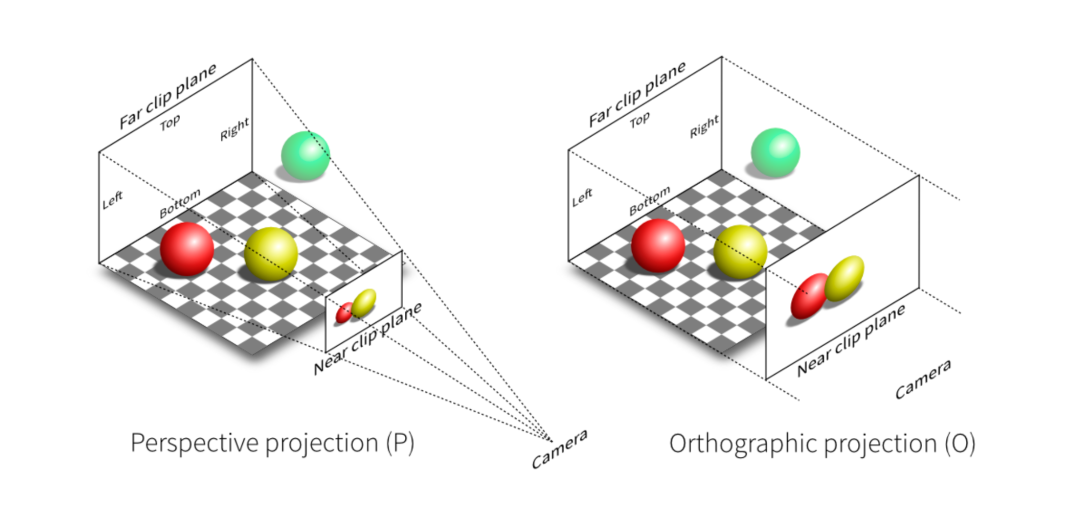
图2 透视投影 & 正交投影

对比正交投影和透视投影效果可以发现，透视投影的结果会有近大远小的效果，而正交投影不会。正交投影中，以平行线投射方式投影，在工程制图等场景应用广泛。透视投影这种近大远小的效果和人眼成像效果基本一致，后面主要针对透视投影讲解。也正是因为这种效果，才有了"道理我都懂，可是为什么鸽子这么大"这个梗。绿色的球在视野之外，会被裁剪掉。透视投影本质就是对一个平截头体及平截头体里的物体（图2左半边虚线内部分，包含红球和黄球）做变换，这时候平截头体会被压成长方体(图3-1)，变换后的物体也包含在这个长方体中，最终长方体标准化生成[-1, 1] ^ 3标准正方体(图3-2)，然后再针对[x, y]平面做投影，投影过程中z轴作为深度覆盖参考。

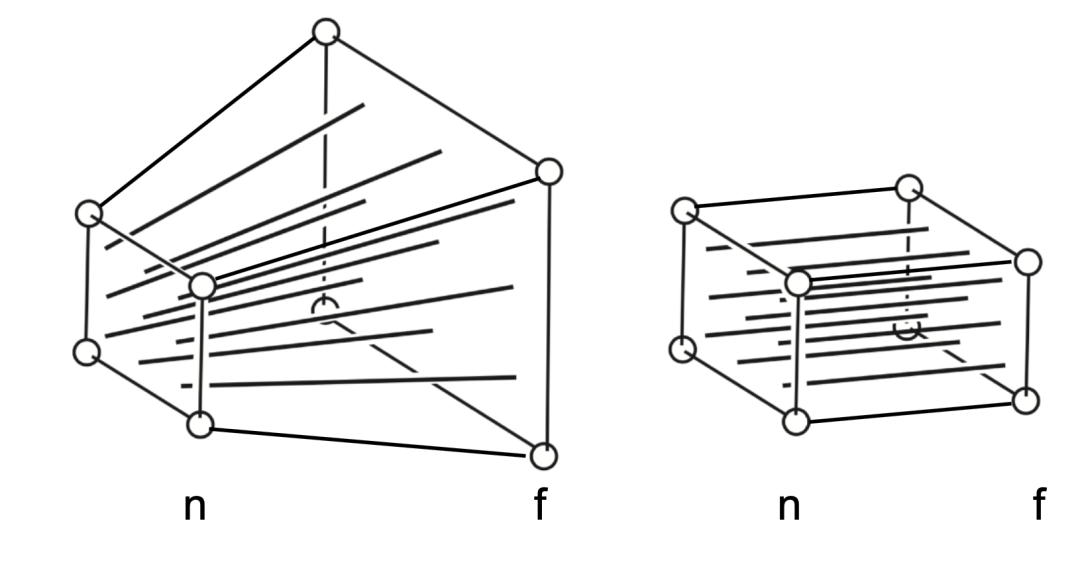
图3-1 透视压缩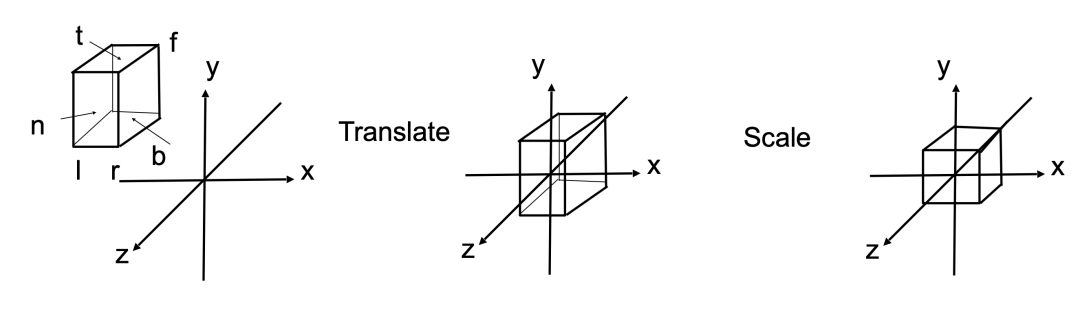



图3-2 坐标标准化

再看下面两个效果图：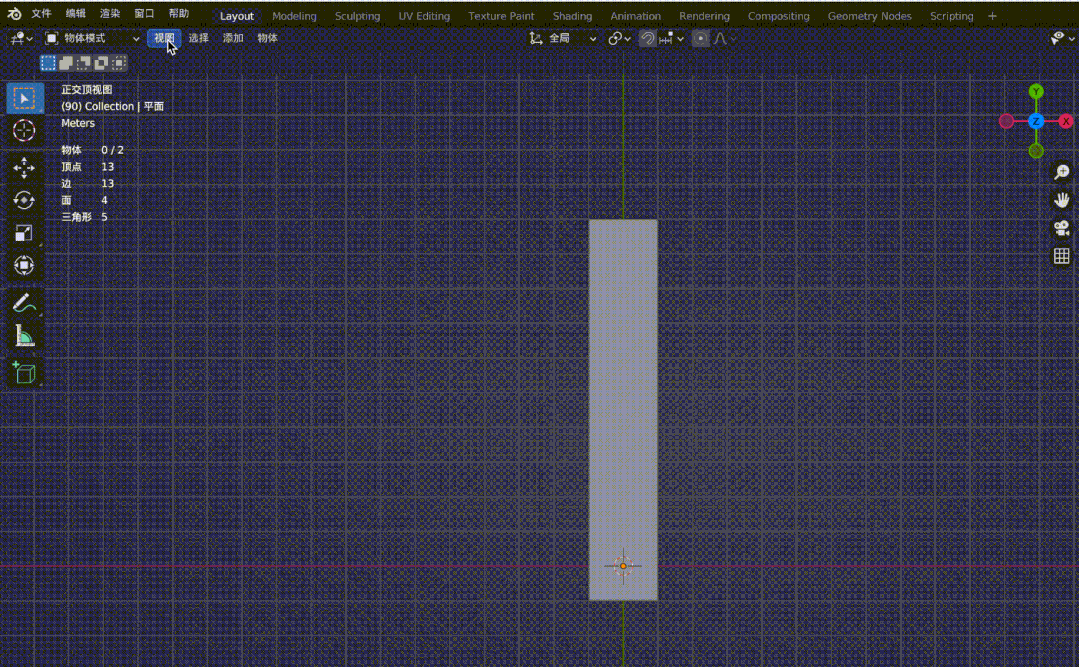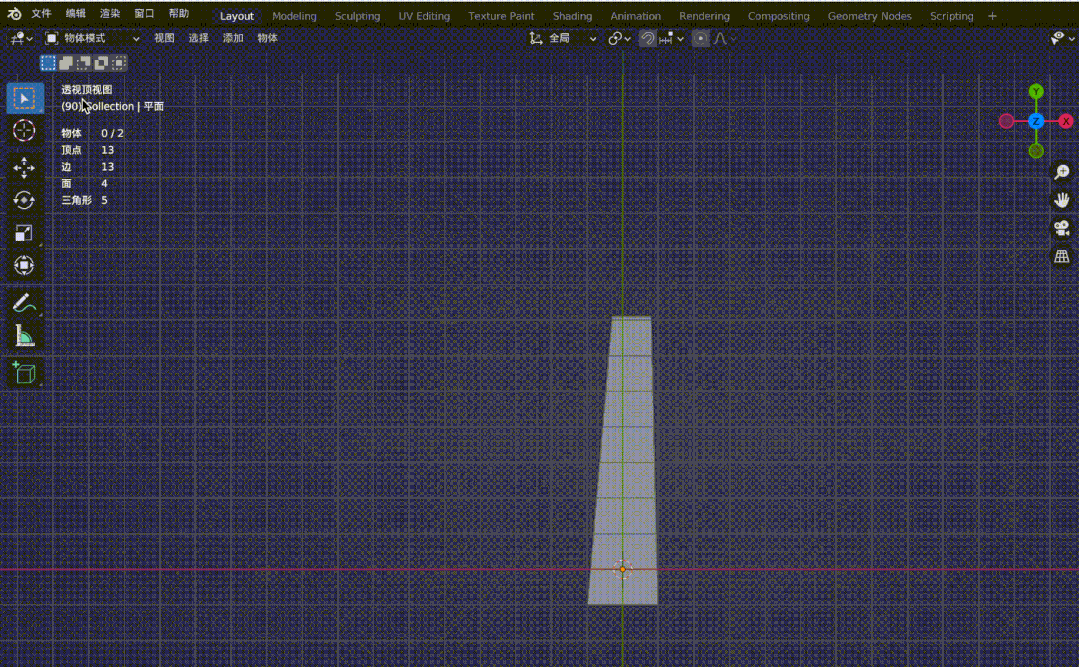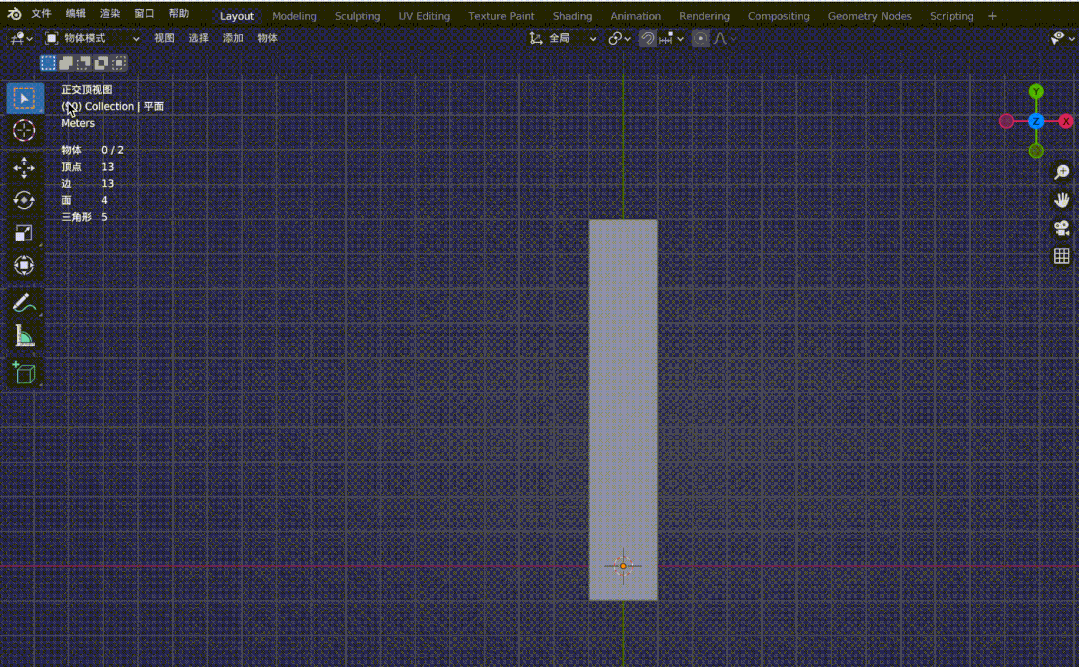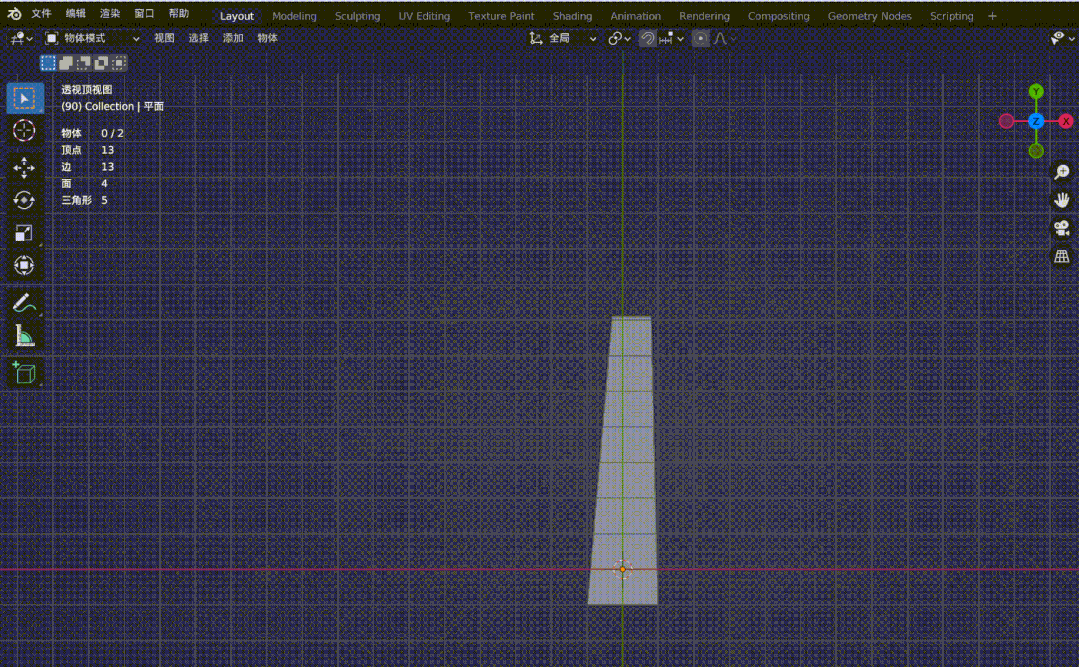




图4-2

图4-1铁轨是平行的，但在透视投影的作用下，原本的平行线在远处变得相交。图4-2是观察正交视图和透视视图来对比两者区别，同样，在透视投影下，会有近大远小的效果，（图中四个顶点坐标分别为(-1, 10, -20), (1, 10, -20), (-1, -1, 0), (1, -1, 0)，z 轴俯视观察。

关于透视投影部分还有以下几点说明：

这里没有推导透视投影矩阵，而是直接给出了矩阵变换后的效果图，一是希望读者从直观上感受透视投影的效果，二是文章主要内容是光栅化过程的概述，推导不作为重点。如果想了解透视投影的原理，可以学习《GAMES101》或者从《Fundamentals of Computer Graphics》中寻找答案

针对透视投影的效果，最终呈现出来的就是近大远小的视觉效果

无论是正交投影还是透视投影，我们目前做的都是针对几何图形的变换，但是最终的目的是屏幕显示，屏幕显示必然涉及到分辨率和屏幕尺寸。所以，正交投影和透视投影的最后一步都是标准化(图3-2)，最终得到[-1, 1] ^ 3的标准立方体。屏幕上的窗口可以是动态变化的，如：400 x 600，600 x 800等，标准化后通过简单平移 + 缩放即可完成视口变换。

结合我们的模型，对两个三角形做透视投影（图5-1），可以看到两个三角形都在平截头体中，做透视投影后（乘透视矩阵）会先得到标准立方体，然后向[x, y]平面投影（暂时忽略z），得到具有近大远小效果的图（图5-2），图5-2动态比对正交投影和透视投影差别，可以很明显看到透视投影之后，z绝对值大的三角形会变小很多。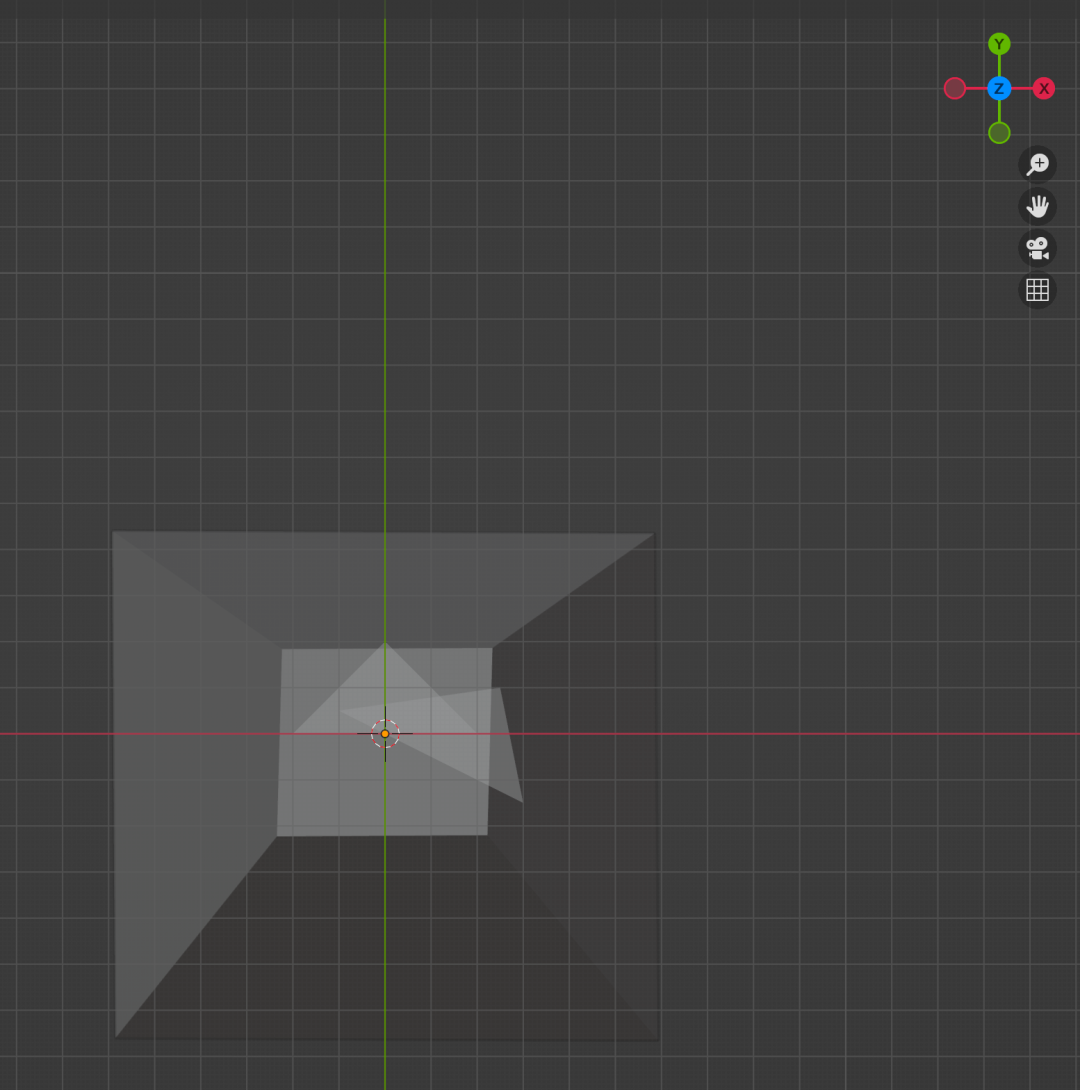



图5-1 包含在平截头体中的三角形

图5-2 最终显示的三角形(透明)

光栅化 & 着色

在透视投影之后，得到的是[-1, -1] ^ 3标准立方体，这一小节要讲的是如何将这个标准立方体投影并绘制在屏幕上。具体过程如下图所示。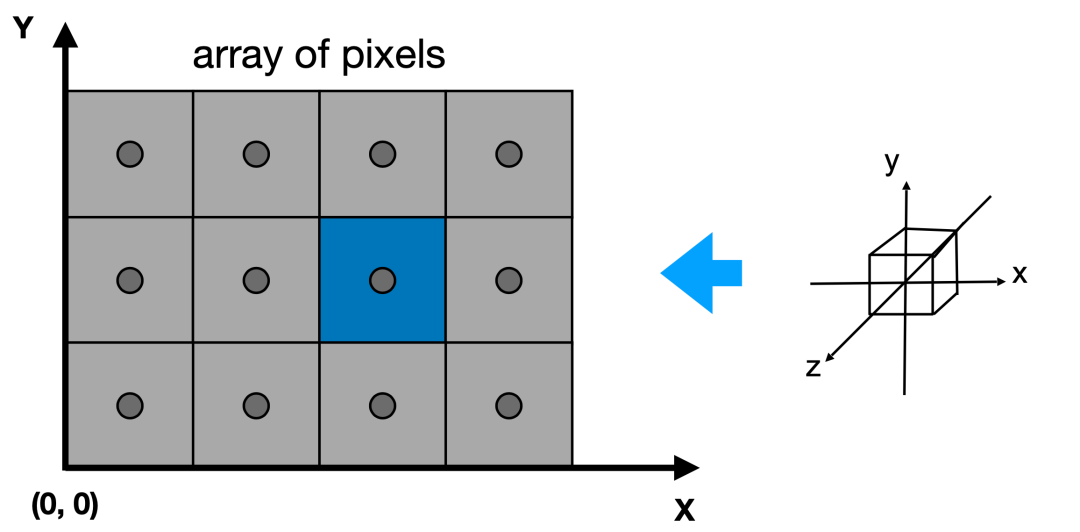

图6-1

图中有如下两点需要注意：

这里先对屏幕做个简单的抽象，将各个像素抽象为正方形，像素中心即为正方形中心，每个小格子就是一个像素，每个小方格子为 1 * 1，像素位于中心，坐标为(x + 0.5, y+0.5)

上一小节提到了透视投影之后，会标准化成 [-1, 1] ^ 3 的标准化立方体，这时先忽略 z 坐标，根据立方体中各个点的 [x, y] 坐标投在屏幕上。当前的[x, y]是标准化坐标，需要做个简单的平移 + 缩放操作，将 x -> width，y -> height，其中 width、height 代表的屏幕中显示窗口大小，这一步叫做视口变换。

回到我们开始的模型，两个三角形，共有 6 个顶点，这里假设所有的图形都不会被裁剪，我们假设三角形三个顶点在在经历透视投影 --> 标准化 --> 视口变换后的坐标与屏幕坐标关系如下图所示（这里是效果示意图，并不是按照上文模型中的坐标得出）：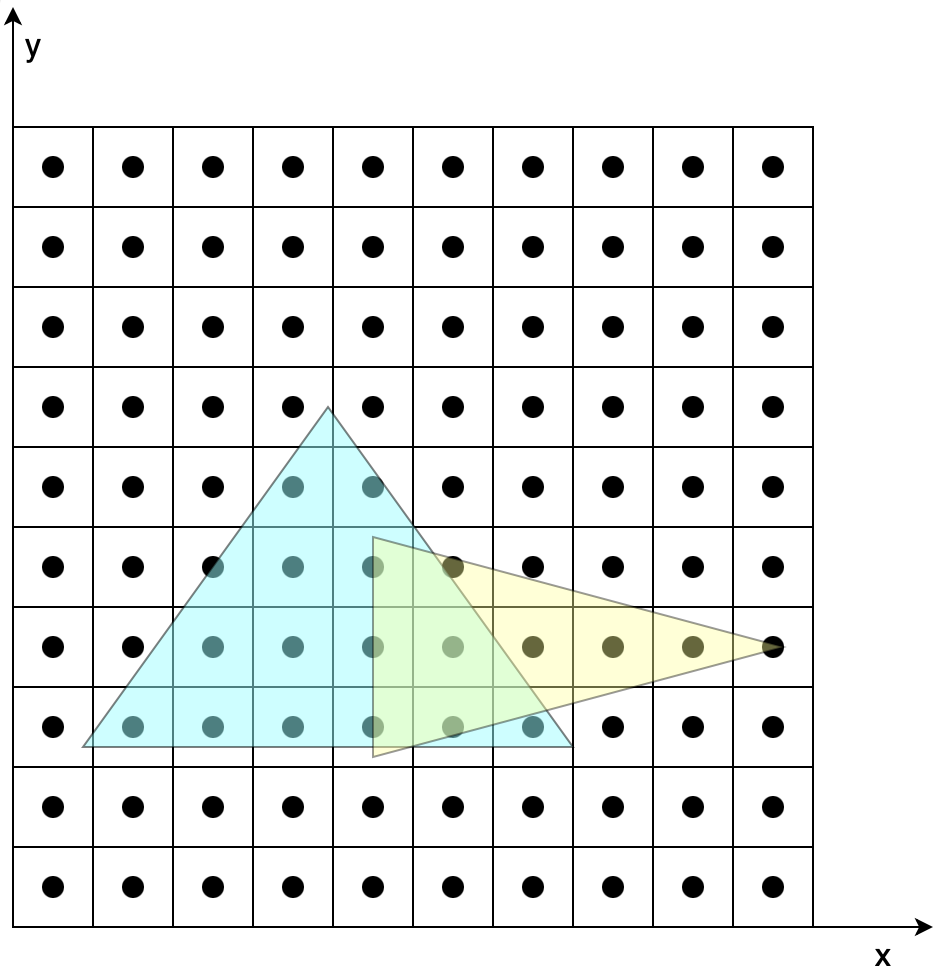

图7-1 投影示意图

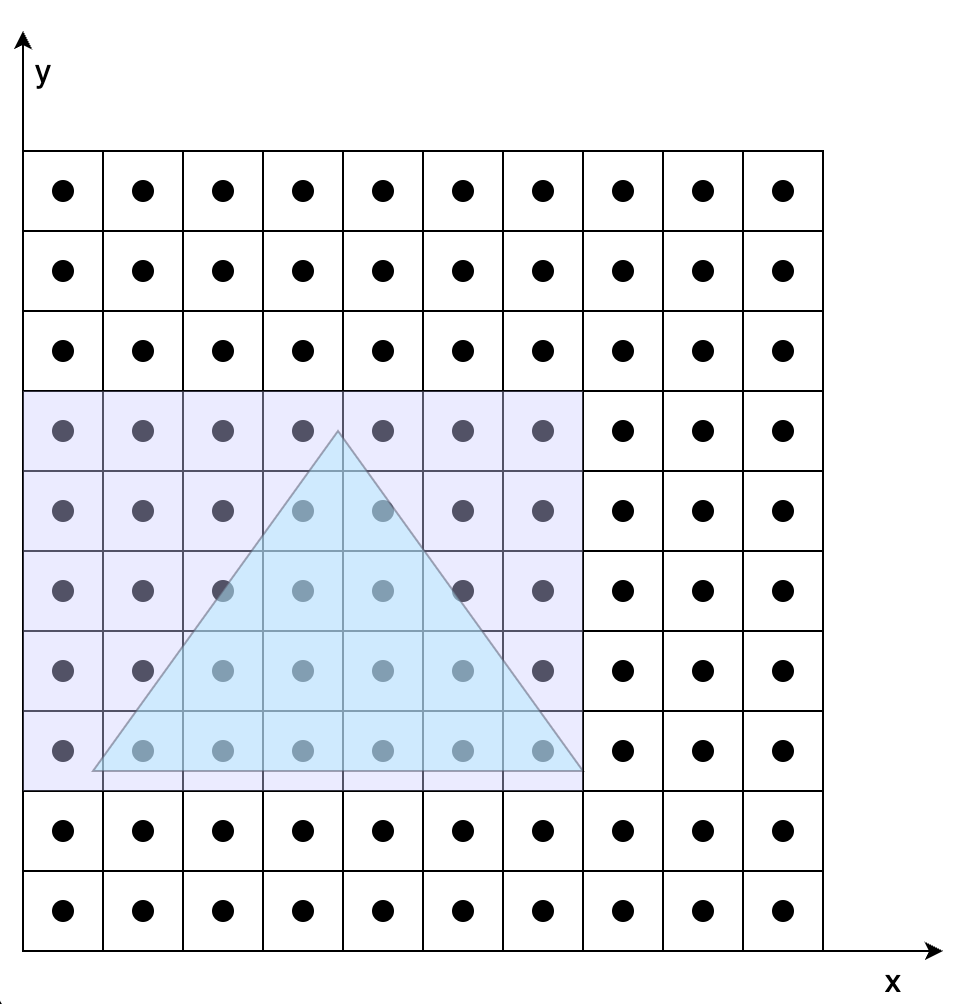
图7-2 包围盒光栅化

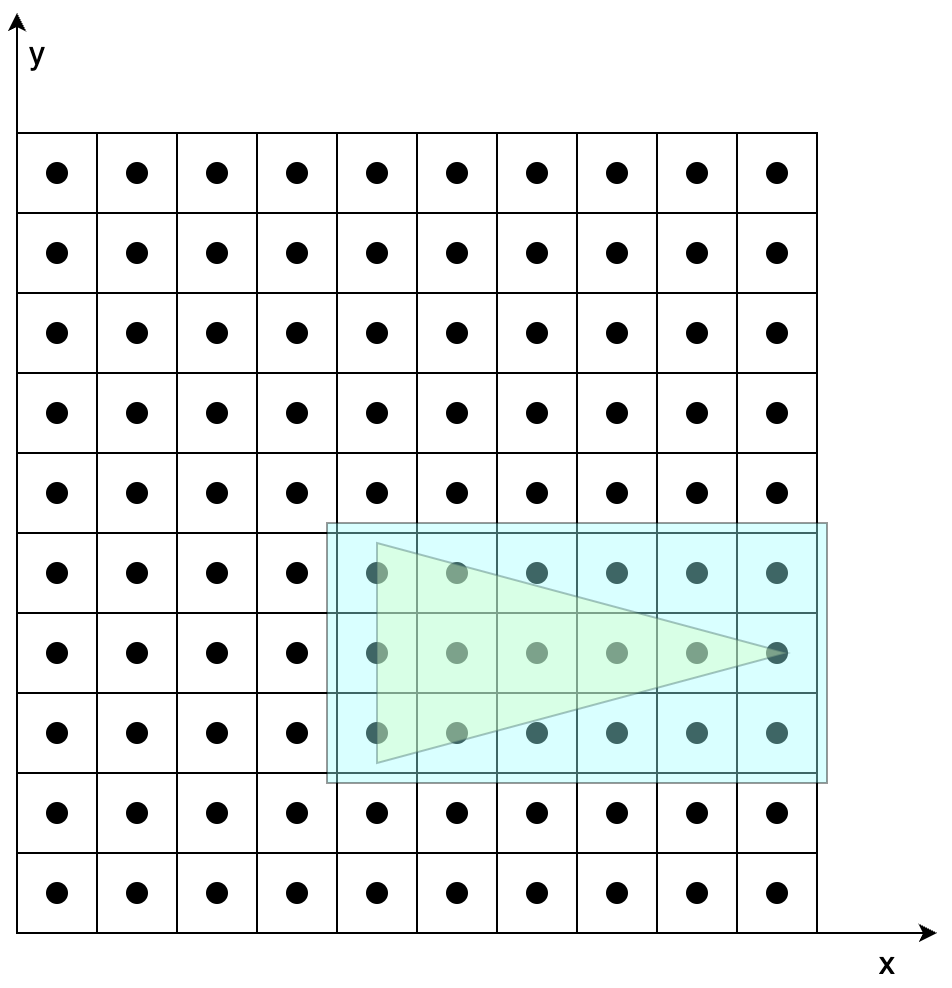
图7-3 包围盒光栅化

图7-1在不考虑覆盖的情况下，根据两个三角形各自顶点变换后的结果，确定两个三角形的位置。图7-2、7-3是在确定三角形位置后，根据三角形覆盖的像素对其着色。具体步骤如下（以图7-2为例）：

首先根据投影后三个顶点的范围确定一个包围盒，这么做的好处是减少搜索范围。

确定了包围盒后，依次判定包围盒中的像素是否在三角形内，这里可以用向量叉乘方法，根据叉乘方向是否同向判定。

对于包含在三角形内的像素，对其进行着色。着色过程中，涉及到纹理坐标、法向量等要素的计算，图7-2中我们知道投影之后的三个顶点坐标、纹理坐标、法向量，但是无法获得三角形内任一点的这些数据，这时候就会用到三角形的重心坐标，利用重心坐标通过插值的方法获得三角形内任一点的数据。比如已知三角形三个顶点的纹理坐标(u, v)，想知道三角形内任一点的纹理坐标，就可以通过该点的重心坐标获取，有一点需要切记，这里所说的重心坐标不是投影后的，而是在做透视投影之前的重心坐标，如果要用投影后的重心坐标，需要做修正。对于三角形内法向量计算也是相同道理。

不过上面的方法仍然存在两个问题：

图7-2、7-3考虑的都只针对自身三角形的光栅化，对于两个三角形的重叠部分没有考虑，后面讲的深度缓冲会解决这个问题。

在判定像素与三角形位置关系时，我们判定的是小方格中心点与三角形关系，即使中心点不在三角形内，像素的小方格子仍然会被三角形覆盖，那么小格子是标记为不亮、还是按照被覆盖的面积来着色，这块如果处理的不好很容易出现锯齿，这里就需要反走样技术，这里不再阐述。

深度缓冲

在透视投影之后得到一个标准正方体，在向 x、y 确定平面投影时会遇到这样的情况，对于两个不同顶点，x、y 相同，z 不同，这时候就要借助深度缓冲方法。不考虑透明效果，上述两个顶点，谁距离摄像机近，后面的就会被遮挡。具体方法如下。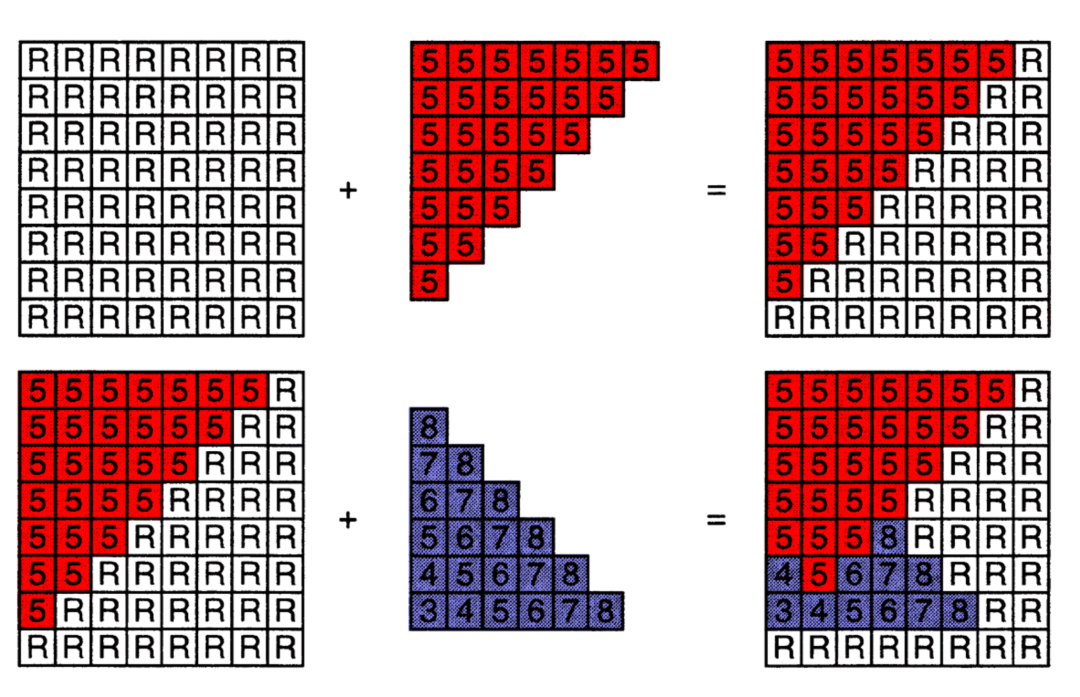

图8-1 深度缓冲原理

在光栅化过程中，被着色的像素会记录当前点在空间中距离摄像机深度，如果再次被着色的时候，会与之前记录的深度值做比对，如果新的值距离摄像机更近，那么会覆盖掉旧的颜色，否则仍然用旧的颜色。这样就解决了点的覆盖问题，上文仅仅是方法上的阐述，还有很多优化空间，比如我们可以提前深度值的判定，对于被覆盖的点省掉不必要的着色操作。图8-2是实例模型执行深度缓冲后的投影结果。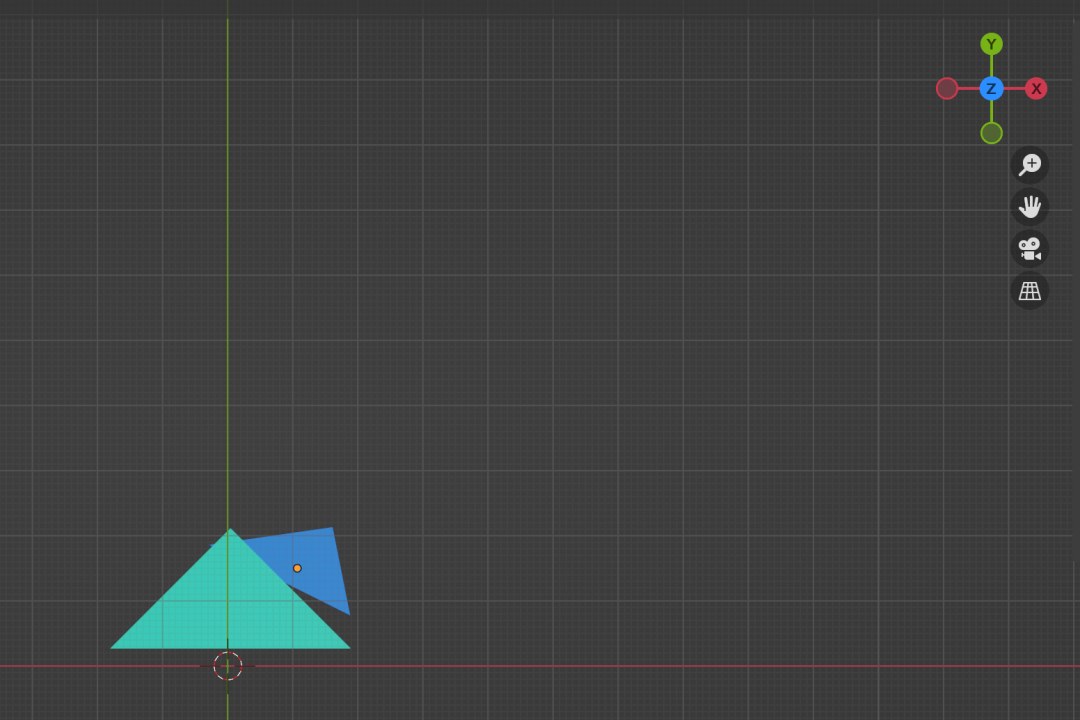

图8-2 最终投影

总结

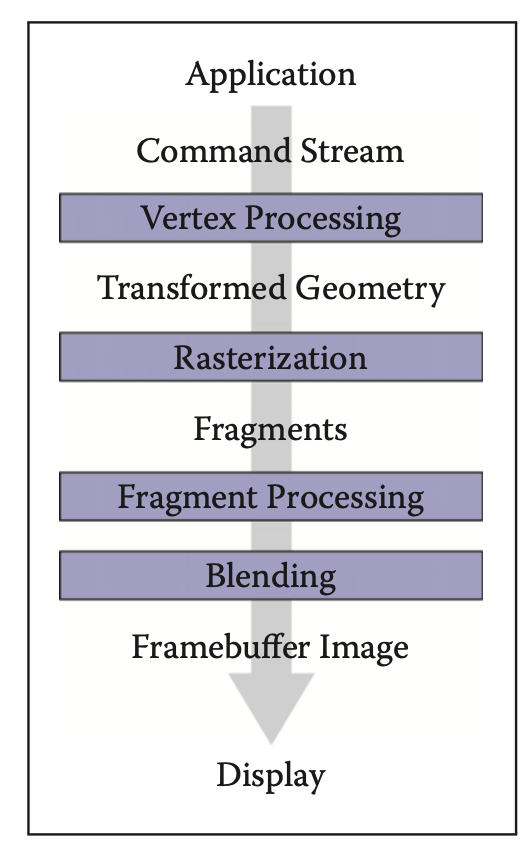
上图是图形管线的主要过程，对照上文例子中的简单模型阐述各个环节工作：

Vertex Processing: 顶点处理，对空间中顶点进行变换，针对我们例子中简化的两个三角形模型，透视投影包含在顶点变换中。

Rasterization: 光栅化操作，对于我们这个例子就是对两个三角形做透视投影 --> 然后向[x, y]平面做投影 --> 视口变换，然后判定投影后的三角形内包含了多少像素。

Fragment Processing: 像素着色，例子中就是针对投影后两个三角形内的像素进行着色，这里与光照、纹理映射相关，对于三角形任一点的纹理坐标、法向量可以通过三角形顶点的这些信息及三角形重心坐标（透视投影前）计算得到。

Blending: 混合上屏，将最终混合结果填充到图形缓冲区，进而刷到屏幕。

审核编辑：汤梓红