相位型空间光调制器的校准

文章来源：锐光凯奇raycage 作者：蒋式弘

和一般电磁波一样，光波也可以用振幅，相位等特征量来描述。光在通过介质后，这些特征一般会发生变化。空间光调制器就是用来改变光波的这些特征的。空间光调制器含有许多独立单元，每个单元都可以接受电信号的控制，利用物理效应如电光效应，磁光效应等改变自身光学特性，从而对照明在其上的光波进行调制。空间光调制器分为两大类，振幅型和相位型，顾名思义就是用来改变光波的振幅或相位的器件。本文仅讨论相位型空间光调制器，并假定纯相位型空间光调制器对光波的振幅没有影响。纯相位型空间光调制器具有实时调制光束相位的功能，是全息投影，光束整形，光学镊子，光学信息处理和衍射光学等应用的重要器件。

相位型空间光调制器工作原理

纯相位型空间光调制器具有实时调制光束相位的功能，是全息投影，光束整形，光学镊子，光学信息处理和衍射光学等应用的重要器件。空间光调制器含有许多独立单元，每个单元都可以接受电信号的控制，利用物理效应如电光效应，磁光效应等改变自身光学特性，从而对照明在其上的光波进行调制。

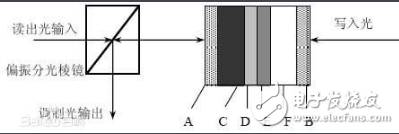
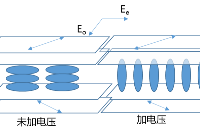
目前利用液晶材料的空间光调制器占有主导地位，典型的液晶材料有扭曲向列型TN（Twisted Nematic），铁电液晶FLC（Ferroelectric Liquid Crystal），硅基液晶LCOS（Liquid Crystal on Silicon）。如图1所示，以硅基液晶为例，光线垂直入射到镀有增透膜的保护玻璃，导电层（通常为氧化铟锡ITO）和取向膜（通常为聚酰亚胺PI），再经过液晶材料，取向膜，到达介质高反膜后被反射。高反膜下面的导电层与上面的导电层起到连接驱动信号的作用，不同的是下面的导电层是由硅基板上一个个微小独立单元组成。当加载一定驱动电压后，液晶层中会形成电场，使液晶分子排列方向发生改变，见图2。当驱动电压为零时，液晶分子排列方向回复到初始状态，如图1的水平方向。当在各个独立单元上施加不同电压时，平面入射光经过每个单元（像素）后便产生不同的相位延迟。经过垂直排列液晶分子的光线传播速度最大，光程最小。反之，经过水平排列液晶分子的光线传播速度最小，光程最大。平面光波经过调制后的出射波面如图3所示。

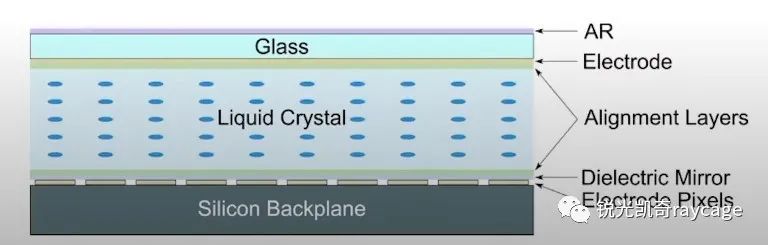
图1 驱动电压为零时（FromThorlabs Webinars）

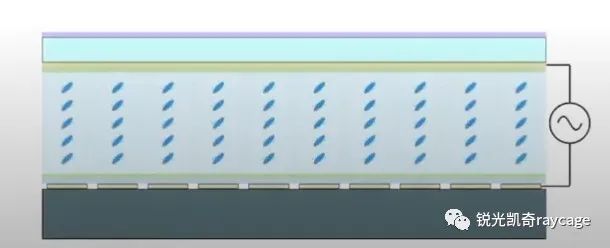
图2 施加驱动电压时（FromThorlabs Webinars）

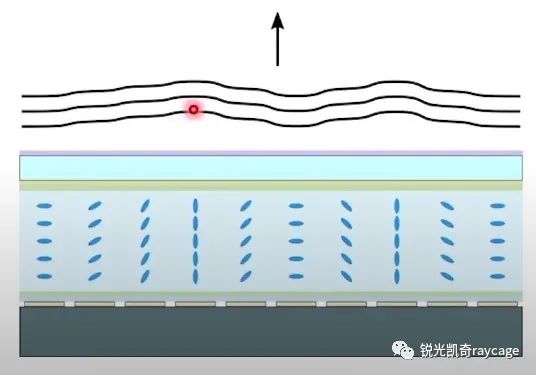
图3 经调制后的出射波面（FromThorlabs Webinars）

相位调制曲线的测量

在理想情况下，各像素的相位变化对驱动灰度值的响应为一直线，但由于制造过程中不可避免的误差和外部环境的影响，空间光调制器存在空间不均匀性，即每个像素对于相同驱动灰度值的相位响应不完全一致，而且每个像素的相位变化相对于驱动灰度值的变化是非线性的[1]。所以空间光调制器在使用前必须经过校准，通过相位补偿校正非线性误差，使各像素的相位调制曲线为一直线[2]。

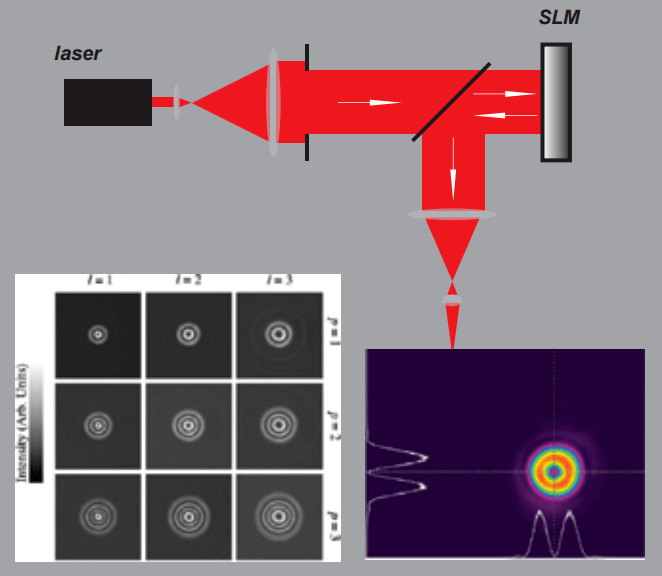
为了校正非线性误差，首先要测量出空间光调制器的相位调制曲线。测量系统光路如图4所示。波长为λ的激光经过空间滤波和扩束产生均匀照明光束，经过透光轴和SLM快轴成45°夹角的起偏器，再经分光镜入射到SLM。光束经SLM调制后的出射光束为振动方向相互垂直，传播速度不同的参考光（o光）和调制光（e光）。这两束光再经过和快轴成-45°夹角的检偏器，便能够产生干涉。

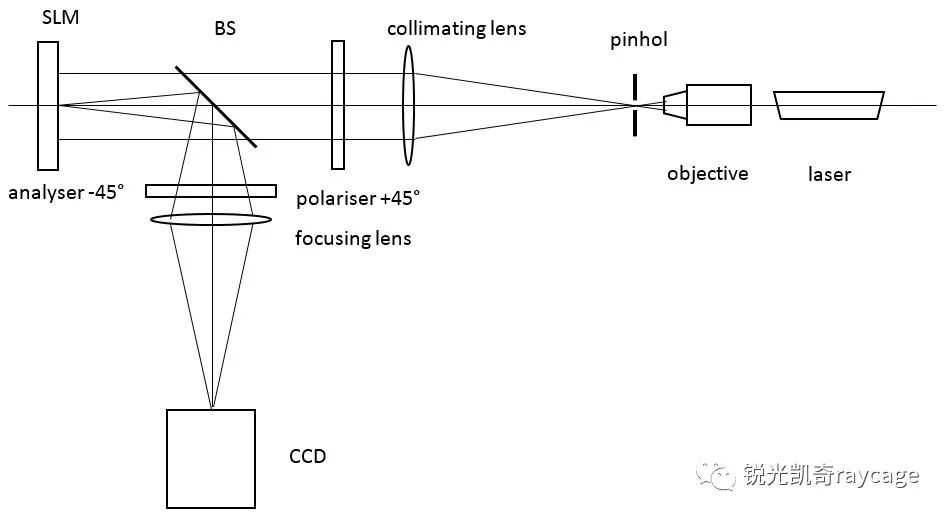
图4 相位调制曲线测量系统光路图

干涉场上某点的光强度为

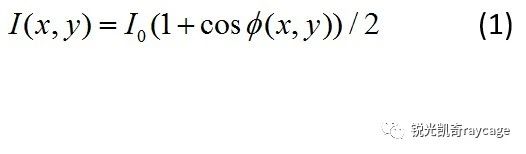
其中相位差φ=2π(no-ne)l/λ，no和ne分别为参考光和调制光的折射率。如果使SLM驱动电压值发生连续线性变化，那么在CCD相机上记录到的干涉光强度则呈现余弦变化。

以Holoeye Pluto-2-VIS-016液晶空间光调制器为例，令驱动灰度值以5为步长，从0增至255，如视频1所示。CCD相机记录的一系列干涉光强度图像如视频2所示。

利用方程(1)测量相位调制曲线的过程见图5。由于SLM各像素对于相同驱动灰度值的响应不一致，以及CCD相机的噪声，左上图给出SLM整个表面的强度平均值以及标准偏差，右上图是去除直流分量I0后的强度平均值，左下图是作希尔伯特变换[3]后得到的相位，最后对相位解缠绕，就得到了右下图所示的相位调制曲线。

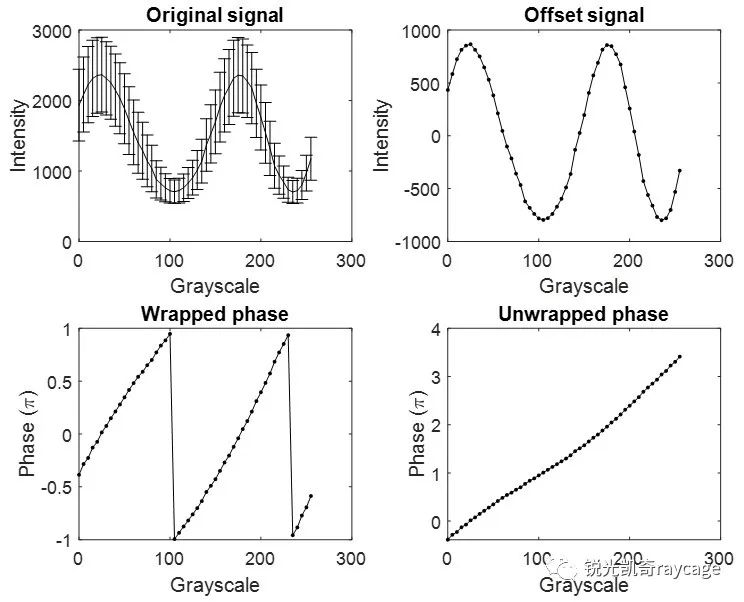
图5 原始相位调制曲线

相位调制非线性校正

从调制曲线可以看出，液晶空间光调制器的相位随驱动灰度值的改变呈现明显的非线性变化，因此需要对相位调制曲线进行补偿和校正。这里介绍比较常用的反插值法[4]，通过建立实际输入灰度值和驱动灰度值之间的非线性映射关系，使输入灰度与调制相位之间满足线性的对应关系。在原始相位调制曲线中，相位和驱动灰度之间的关系记为：

对以上函数进行线性拟合，以构造一个线性函数:

对y’进行反插值，便得到实际输入灰度值查找表（LUT）

图6为原始相位调制曲线和拟合后得到的线性函数。图7为实际输入灰度值和驱动灰度值的关系或查找表。用反插值法校正非线性的MATLAB代码见附录。在图4所示的测量装置上，用公式(4)得到的一系列实际输入灰度值驱动SLM，用CCD相机记录干涉光强度。再利用方程(1)得到的校正后的相位调制曲线如图8所示，比较图5，可见非线性得到了校正。

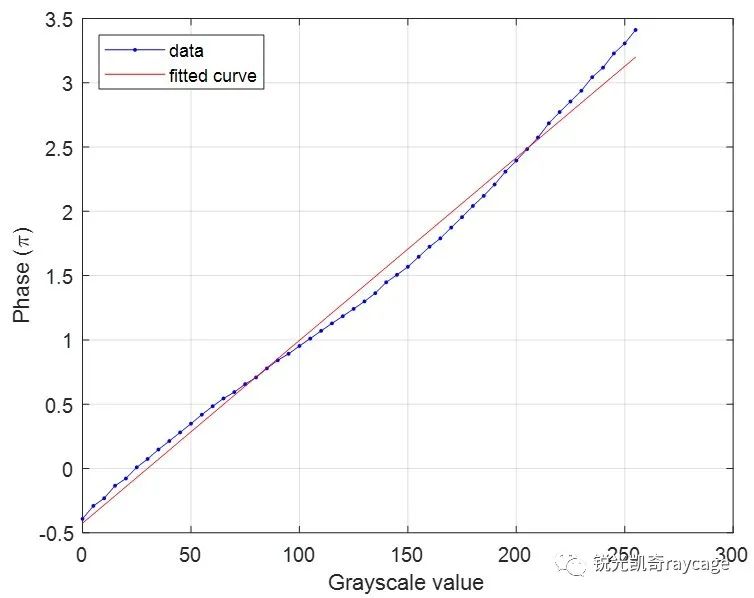
图6 原始相位调制曲线和拟合直线

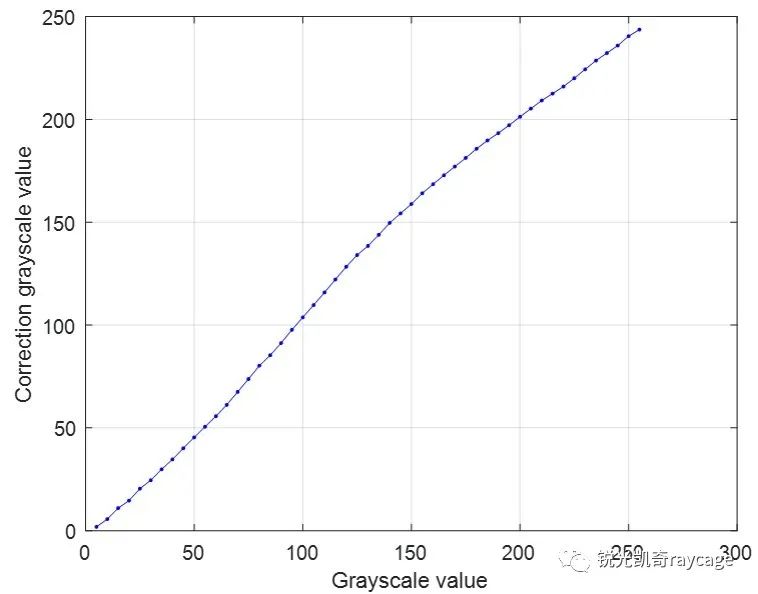
图7 实际输入灰度值和驱动灰度值的关系（LUT）

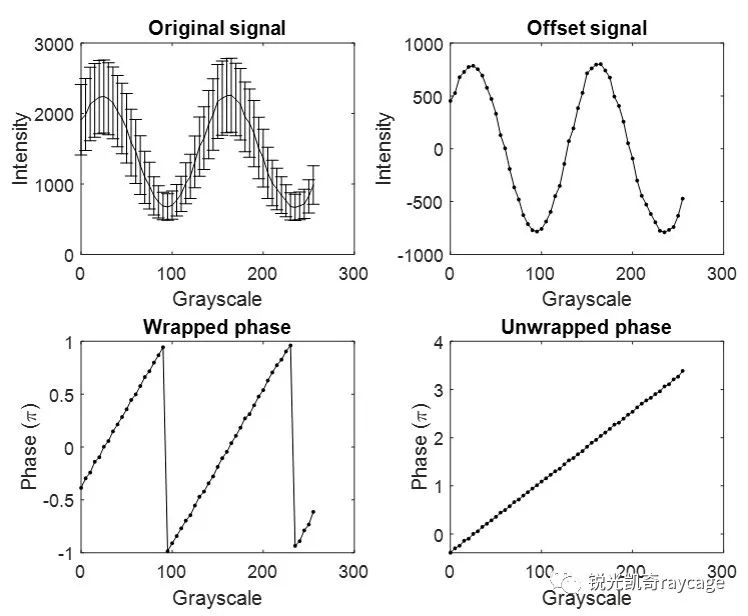
图8 校正后的相位调制曲线

结语

相位调制线性度是液晶纯相位空间光调制器的重要特性之一。在某些应用中，比如作为衍射器件使用时，线性度的好坏会对衍射图形的质量产生决定性的影响，因此在使用前必须对SLM进行所谓校准（calibration）。在一个均匀的二维灰度值驱动下，没有经过校准的SLM输出的相位往往是一个高低不平的曲面，因此严格来说，必须对SLM上每个像素都进行相位补偿或校正，因此每个像素都有自己的实际输入灰度值查找表。本文为了简单起见，仅对强度平均值进行相位校正，特此说明。

附录：反插值法相位校正MATLAB代码

x = 0255;

y = [-0.39234203,-0.29157189,-0.23207852,-0.13453995,...

-0.078362830,0.0086319931,0.073616728,0.14730585,...

0.21277669,0.28007278,0.34822226,0.41796023,...

0.48390859,0.54430258,0.59411800,0.65596730,...

0.70788610,0.77856773,0.84126735,0.89191860,...

0.95283592,1.0103669,1.0701512,1.1285787,...

1.1846226,1.2414784,1.2993250,1.3638737,...

1.4482110,1.5066255,1.5688090,1.6468172,...

1.7248957,1.7901216,1.8742696,1.9552350,...

2.0423748,2.1206505,2.2093096,2.3094342,...

2.3952017,2.4846230,2.5747743,2.6854355,...

2.7731009,2.8549440,2.9389544,3.0441573,...

3.1187348,3.2292576,3.3070712,3.4119809];

figure(1)

plot(x,y,'-b.')

grid on

hold on

% linear fit

cf =fit(x',y',fittype('poly1'));

y1 =feval(cf,x);

plot(x,y1,'-r')

legend('data','fittedcurve','Location','northwest');

xlabel('Grayscalevalue')

ylabel('Phase(pi)')

% inverse interpolation

x1 =interp1(y,x,y1);

figure(2)

plot(x,x1,'-b.')

grid on

xlabel('Grayscalevalue')

ylabel('Correctiongrayscale value')

审核编辑：汤梓红