锂电池的内部的电化学反应复杂,电化学反应参数并不能直接测量,因此需要依赖动力电池模型来对表达电池的动态特性。目前,动力电池模型主要有两大类,一类为对电池相关性能进行建模的等效电路模型,基于数据驱动和归纳方法相结合的数值建模技术,采用测量技术获取相关的参数;另一类为基于电化学动力学过程建立的机理模型。
一、等效电路模型
等效电路模型使用一个理想电压源来模拟电池正负极材料之间的电位差,表现电池的电动势特性;其次,用内阻来模拟电化学反应和离子运动的过程中会产生的阻力。由于形成的机理不同,电池的内阻又可以进一步划分为欧姆内阻和极化内阻,欧姆内阻是由电极材料、电解液、隔膜内阻及接触内阻组成的;极化内阻是电化学反应过程中发生极化现象时产生的,可细分为电化学极化内阻和浓度极化内阻,用来模拟极化以及极化消去过程中的电池特性。电化学极化也称活化极化,是由于正负极活性物质发生的电化学反应速率小于电子运动速率引起的极化,响应时间微秒级;浓度极化是由于反应物消耗引起电极表面得不到及时补充(或是某种产物在电极表面积累,不能及时疏散),导致电极电势偏离通电前按总体浓度计算的平均值,响应时间秒级。
1.内阻模型(Rint模型)
内阻等效电路模型是最简单的等效电路模型,由一个非线性电压源和一个电阻串联构成,电压源和电阻随电池状态而不断变化,参数的辨识容易,但精度不高,且不能体现电池极化和极化消去过程中电池的动态特性。
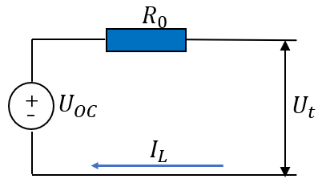
图1内阻模型(Rint模型)
Rint模型公式为:
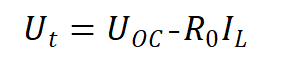
2.一阶RC模型(Thevenin模型)
一阶RC模型包括一个非线性电压源和一个RC环节,用非线性电压源来描述电池的稳态开路电压UOC,用欧姆内阻R0以及电阻Rp与电容Cp并联环节来描述瞬态响应。一阶RC模型相较于内阻模型,能够模拟出电池的动态过程。
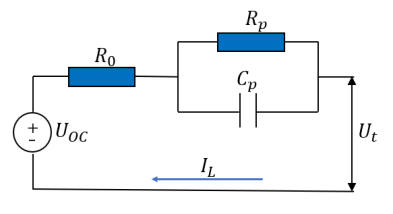
图2一阶RC模型(Thevenin模型)
Thevenin模型公式为:
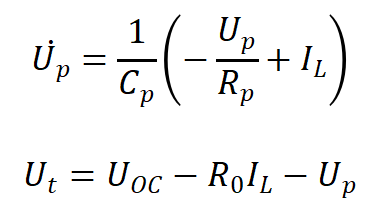
该方程可以写成离散递推形式:
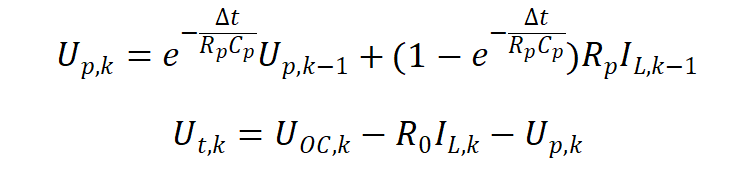
RpCp为极化时间常数,对应着极化的响应时间;∆t对应着采样时间间隔。
3.双极化模型(dual polarization,DP)
双极化模型包括一个非线性电压源和两个RC环节,与一阶RC模型相似,用非线性电压源来描述电池的稳态开路电压UOC,用欧姆内阻R0以及电阻Rp、Rs与电容Cp、Cs并联环节来描述瞬态响应。双极化模型通过两个RC回路能够更好的模拟电池的动态过程,兼顾电池的瞬态特性和稳态特性。
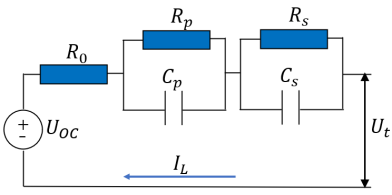
图3 双极化模型(DP模型)
DP模型公式为:
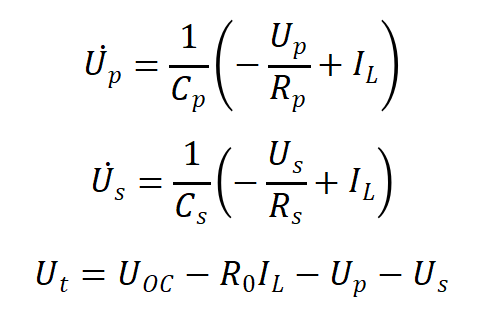
该方程可以写成离散递推形式:
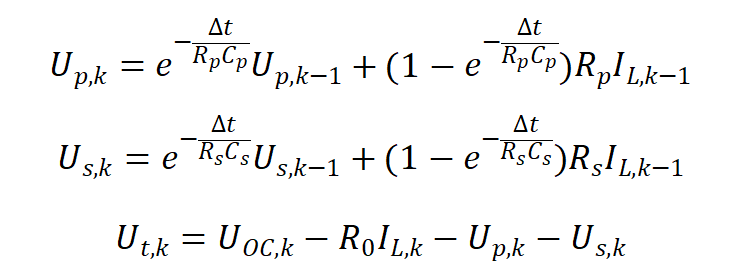
4.PNGV模型(partnership for new generat--ion of vehicles model)
PNGV模型是美国新一代汽车合作计划在2001年《PNGV电池试验手册》中的标准电池模型,也沿用为2003年《FreedomCAR电池试验手册》中的标准电池模型。PNGV模型相较于一阶RC模型,用理想电压源来描述电池的稳态开路电压UOC,增加了一个用来描述负载中电流累计产生的开路电压变化的电容Cs,电容Cs模拟了电池的容量。
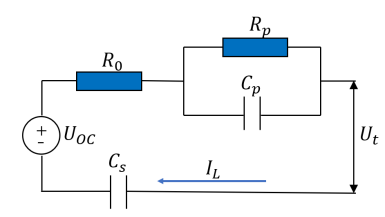
图4 PNGV模型
PNGV模型公式为:
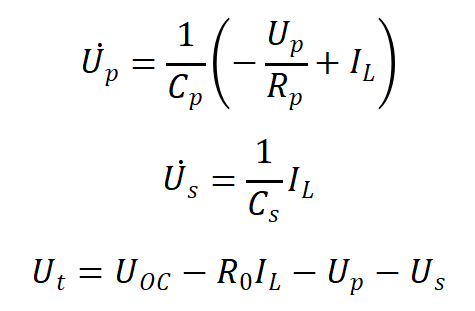
PNGV模型的离散递推形式与其他模型相比,开路电压不作为输入变量:
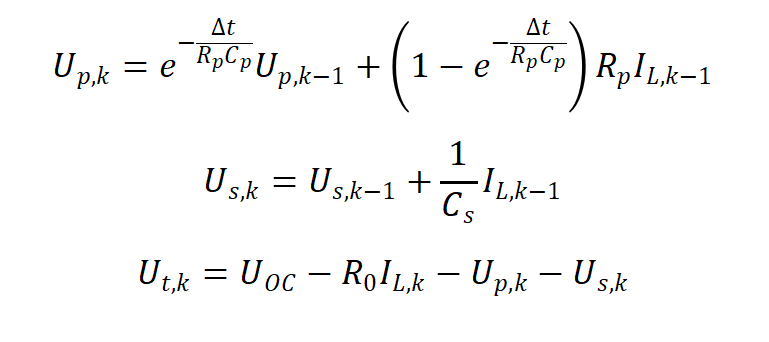
二、电化学模型
1.伪二维模型(pesudo-two-dimensional model,P2D)
P2D模型基于两个关键:物质转移和电荷转移。物质转移发生在在电解质和材料颗粒内部,在电解质中锂离子的移动为液相的扩散与迁移;在材料颗粒内部锂离子的移动为固相的的扩散。电荷转移发生在材料颗粒表面,其核心是通过Bulter—Volmer方程对交换电流密度分析进行分析。P2D模型可描述为5个方程:正、负极固相锂离子守恒方程,正、负极固相电荷守恒方程,液相锂离子守恒方程,液相电荷守恒方程,以及电化学反应方程,忽略其边界条件,模型方程如下所示:
根据Fick第二定理,锂离子固相浓度扩散方程为:
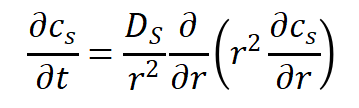
方程的边界条件为:
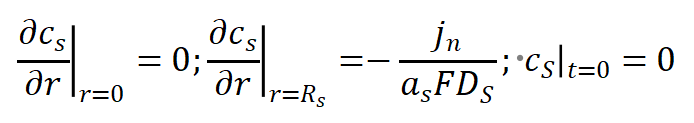
锂离子的液相扩散方程为:
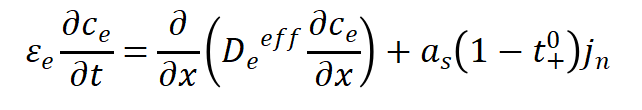
方程的边界条件为:
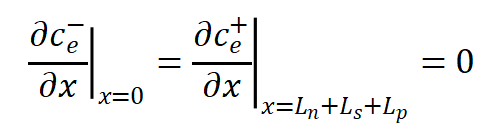
固相电荷守恒方程为:
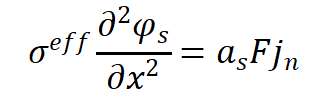
方程的边界条件为:
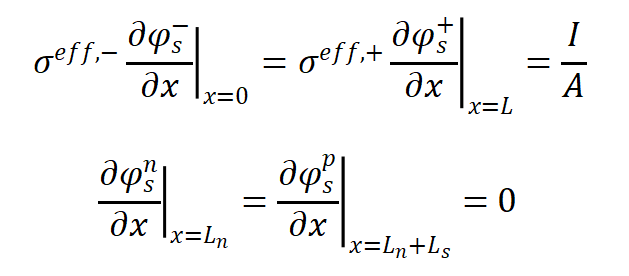
液相电荷守恒方程为:
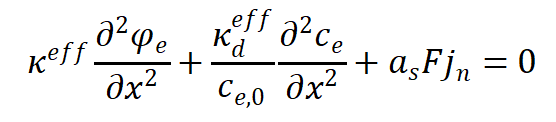
其中,液相有效扩散电导率为:
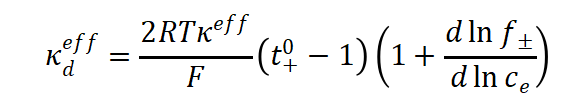
方程的边界条件为:
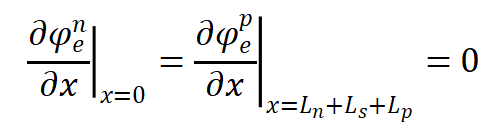
描述固液相交界的电化学反应的Butler- Volmer方程为:
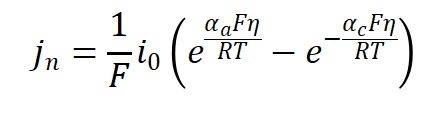
其中表面过电势为:
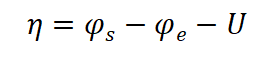
电流密度i0为:
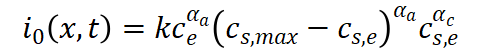
方程中参数意义如表所示:
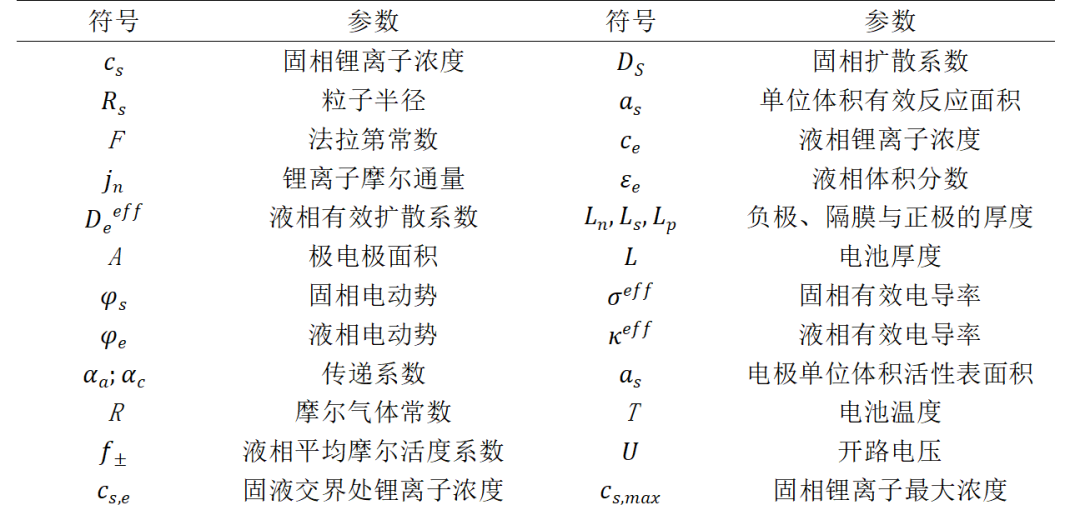
P2D模型是最基础的锂离子电池电化学模型,适用于恒流、绝热系统的电化学模型,将锂离子电池等效为由无数球型固相颗粒组成的电极(正极和负极)、隔膜及电解液组成的三明治结构,能全面系统地描述电池充放电时的工作特性。模型中存在大量偏微分方程与耦合方程,公式复杂且计算量大,且无法获得其解析解,多数情况下用于实验室对电池的特性进行分析。
2.改进单粒子模型(enhanced single particle model,ESPM)
单粒子模型是由P2D模型简化而来的最简单的锂离子电池电化学模型,其假设电解质的浓度和内部电势不发生变化,且物质转移发生在表示电池正极和负极的两个球形颗粒上。
固相浓度扩散方程为:
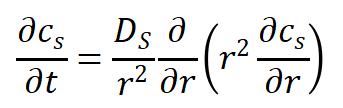
方程的边界条件为:
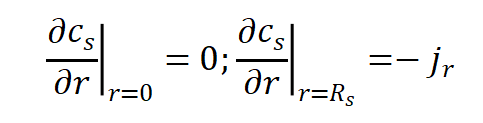
假定电流密度jr为常量,
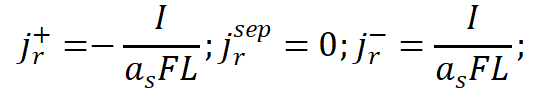
其中,为电流密度,“+,sep,-”分别代表正极、隔膜和负极。
液相电荷守恒方程为:
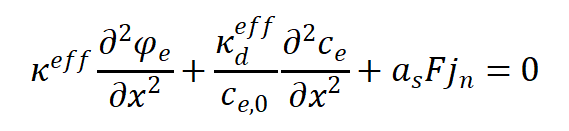
其中,液相有效扩散电导率为:
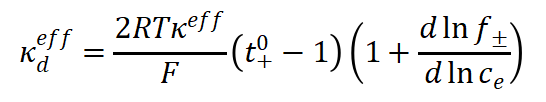
方程的边界条件为:
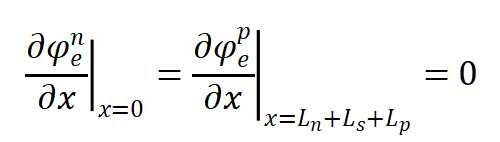
电化学反应的Butler Volmer方程为:
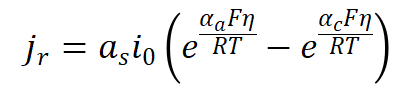
其中表面过电势为:
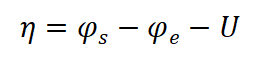
电流密度i0为:
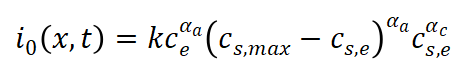
单粒子模型结构简单,计算量小,容易实现在线应用。目前,单粒子模型主要应用于锂离子电池的荷电状态诊断研究。
审核编辑 :李倩
-
锂电池
+关注
关注
260文章
8115浏览量
170276 -
电阻
+关注
关注
86文章
5519浏览量
172102 -
等效电路
+关注
关注
6文章
292浏览量
32768
原文标题:锂电池模型简述
文章出处:【微信号:电源系统智能管控,微信公众号:电源系统智能管控】欢迎添加关注!文章转载请注明出处。
发布评论请先 登录
相关推荐




 锂电池模型简述
锂电池模型简述










评论