本文主要介绍原问题(PRIME PROBLEM)和对偶问题(DUAL PROBLEM),支持向量机优化问题可通过原问题向对偶问题的转化求解。
一、原问题的定义
原问题的定义为:
最小化:f(ω);
限制条件:gi(ω)≤0,i=1~K;hi(ω)=0,i=1~M。
其中,ω为多维向量,限制条件中具有K个不等式(gi(ω)≤0),M个等式(hi(ω)=0)。
二、对偶问题的定义
首先定义函数:L(ω,α,β)=f(ω)+∑αigi(ω)+∑βihi(ω);
该函数向量形式的定义:L(ω,α,β)=f(ω)+αTg(ω)+βTh(ω);
该函数向量形式的定义中,α=[α1,α2,…,αK]T,β=[β1,β2,…,βM]T,g(ω)=[g1(ω),g2(ω),…,gK(ω)]T,h(ω)=[h1(ω),h2(ω),…,hM(ω)]T。
基于函数L(ω,α,β)的定义,原问题的对偶问题定义如下:
最大化:θ(α,β)=infL(ω,α,β);
限制条件:αi≥0,i=1~K。
其中,infL(ω,α,β)为遍历所有ω后,取值最小的L(ω,α,β)。
三、定理一
根据以上定义,可得出定理一:
如果ω*是原问题的解,(α*,β*)是对偶问题的解,则有: f(ω*)≥θ(α*,β*)
该定理的证明如下: θ(α*,β*)=infL(ω,α*,β*)(将α*、β*代入对偶函数的定义)
≤L(ω*,α*,β*)(此步推导由于infL(ω,α*,β*)的取值最小)
=f(ω*)+α*Tg(ω*)+β*Th(ω*)(此步推导根据L(ω,α,β)的定义)
≤f(ω*)(此步推导由于原问题的限制条件gi(ω)≤0,hi(ω)=0,对偶问题的限制条件αi≥0)
四、强对偶定理
将f(ω*)-θ(α*,β*)定义为对偶差距(DUALITY GAP),根据上述定理,对偶差距是大于等于零的函数。
如果g(ω)=Aω+b,h(ω)=Cω+d,f(ω)为凸函数,则有f(ω*)=θ(α*,β*),此时对偶差距等于零。该定理为强对偶定理(STRONG DUALITY THEOREM)。
强对偶定理可更通俗地表述为:原问题的目标函数(f(ω))是凸函数,原问题的限制条件是线性函数,则原问题的解与对偶函数的解相等。
五、KKT条件
若f(ω*)=θ(α*,β*),则有: f(ω*)+α*Tg(ω*)+β*Th(ω*)=f(ω*); 即对于所有的i=1~K,要么αi=0,要么gi(ω*)=0(因为hi(ω)=0)。
该结论被称为KKT条件,KKT分别代表先后独立发现该结论的研究人员Karush、Kuhn、Tucker,该结论在Kuhn、Tucker发现后逐步被推广。
审核编辑:刘清
-
向量机
+关注
关注
0文章
166浏览量
20972 -
机器学习
+关注
关注
66文章
8459浏览量
133371 -
GAP
+关注
关注
0文章
15浏览量
8361
原文标题:机器学习相关介绍(12)——支持向量机(原问题和对偶问题)
文章出处:【微信号:行业学习与研究,微信公众号:行业学习与研究】欢迎添加关注!文章转载请注明出处。
发布评论请先 登录
相关推荐


基于改进支持向量机的货币识别研究
基于支持向量机(SVM)的工业过程辨识
基于向量机随机投影特征降维分类下降解决方案
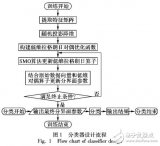
多分类孪生支持向量机研究进展
支持向量机的故障预测模型
什么是支持向量机 什么是支持向量
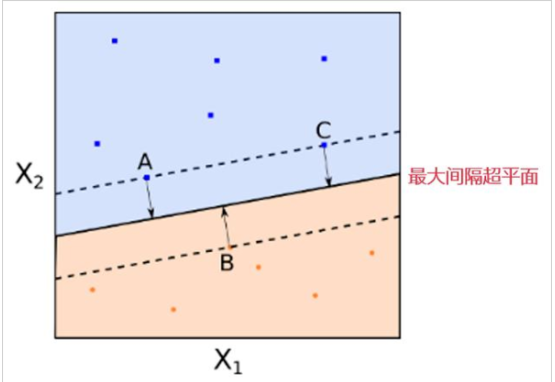




 支持向量机(原问题和对偶问题)
支持向量机(原问题和对偶问题)
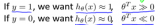










评论