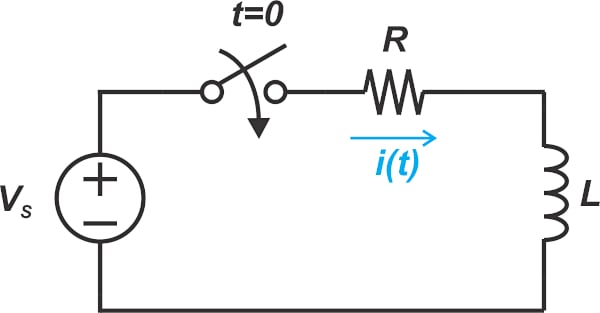
讲了源端发射到终端,用信号反射的观点,去计算源端和终端的电压波形。
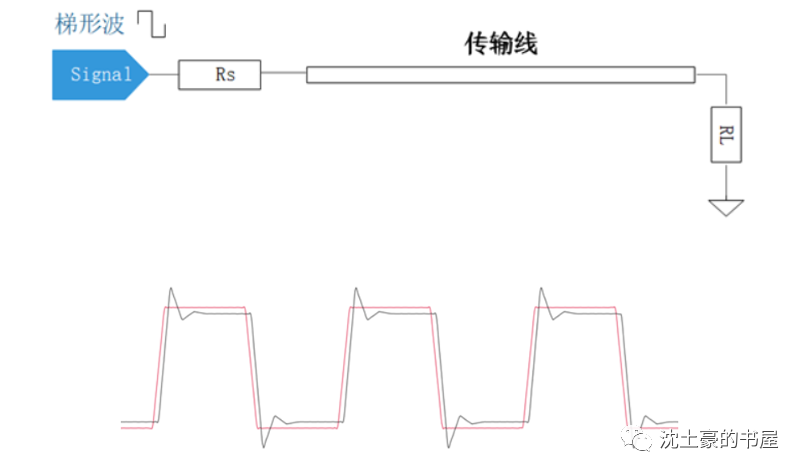
用的是梯形波:
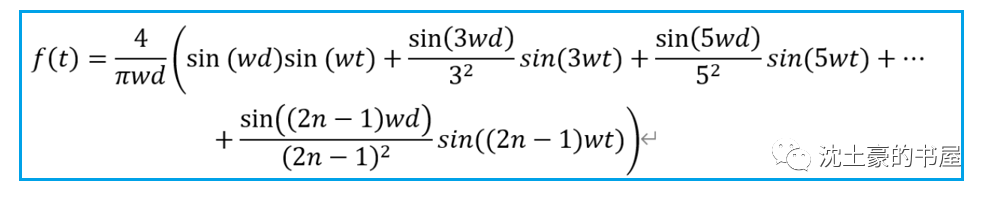
傅里叶级数真的优雅,一般书本上的习题也都是三角波、矩形波,积分起来相对容易。
脑子里突然一热,想把边沿可变+脉宽可控的梯形波,用傅里叶级数分解掉。
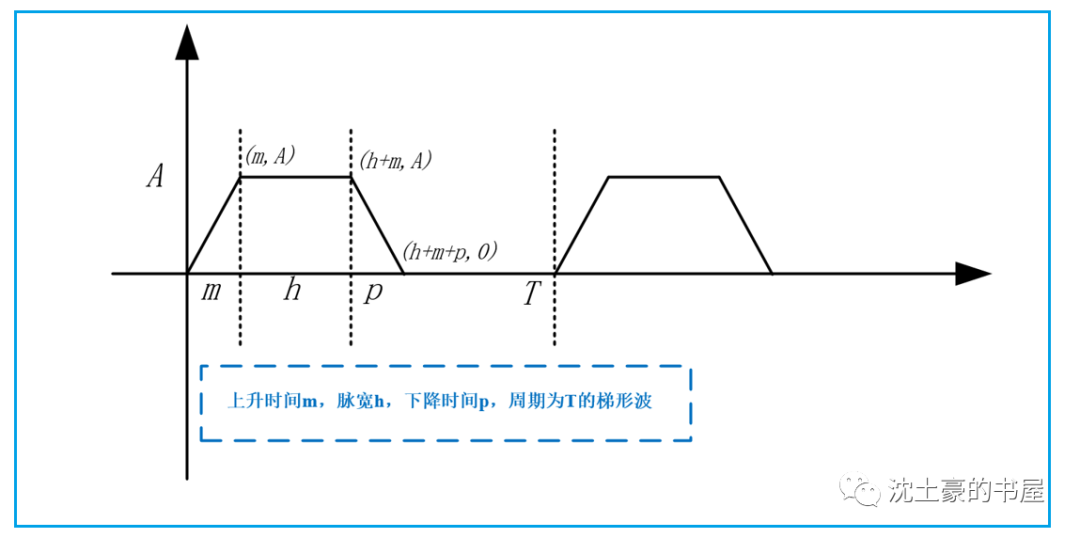
有点飘了,数学底子不行,不会用对称性,积分也不熟练了,没什么技巧,就是死做。
但是积这种边沿可变+脉宽可控的梯形波,是非常有意义的。
因为实际的TX端,边沿不可能无限陡峭,脉宽也要做成可控。这个波形比单纯的矩形波更常用。
Part 02
动手开搞
周五晚上就酝酿了,徘徊退缩了很久想一想还是积一下,网上仅有的资源也几乎只有一个答案,而且边沿不灵活,数学表达式也不是我想要的。
列表达式:
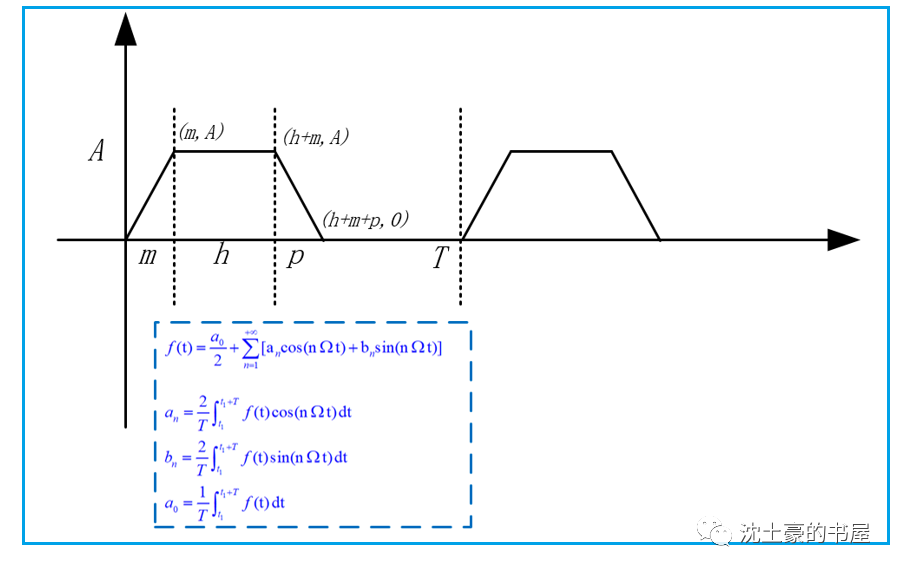
搬出来初中数学老师教的点斜式,梯形在一个周期内的表达式:
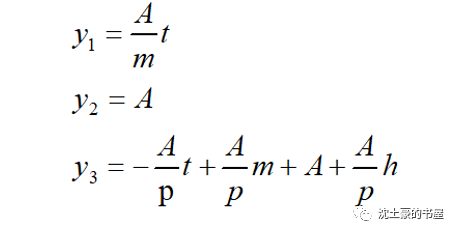
初中数学老师可以先撤了请高中和大学数学老师出山了然后开始漫长的积分:

过程非常的痛苦,不难但是繁琐,实不相瞒持续了3个小时,输完所有公式,从18.30持续纠错到近了22.30,洋洋洒洒7-8页的重复劳动。
Part 03
导入matlab 进行plot
matlab是个高级计算器了,可以帮你验证下积分的结果正确与否。
把word里的公式全部打入matlab文件,看看波图
振幅A=1,周期T=100,上升时间m=10,正脉宽=30,下降时间p=20;
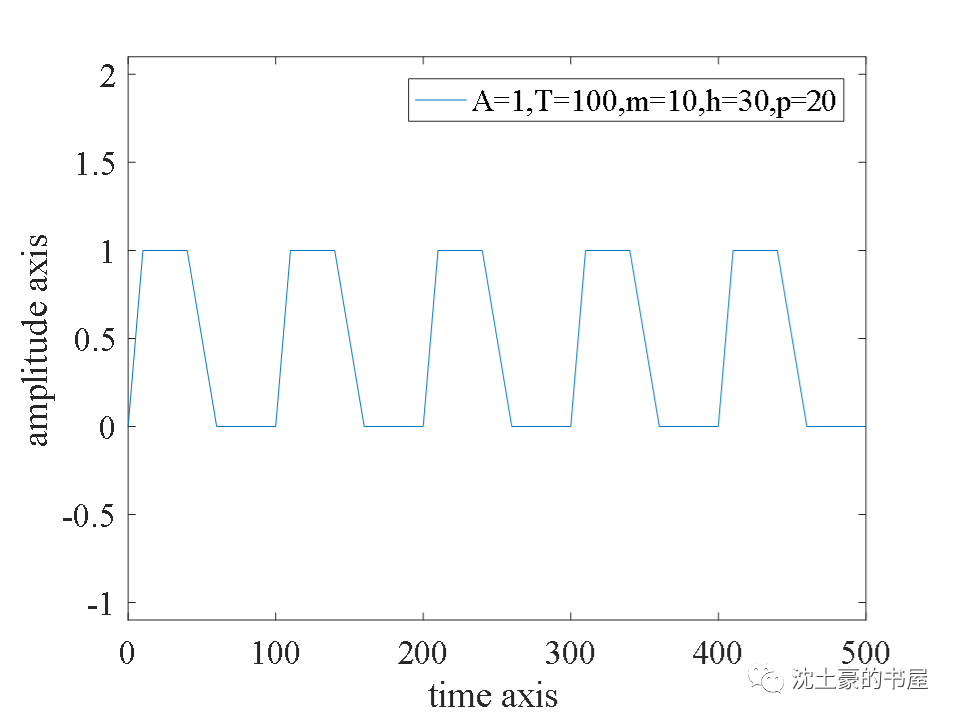
振幅A=1,周期T=100,上升时间m=5,正脉宽=40,下降时间p=5;
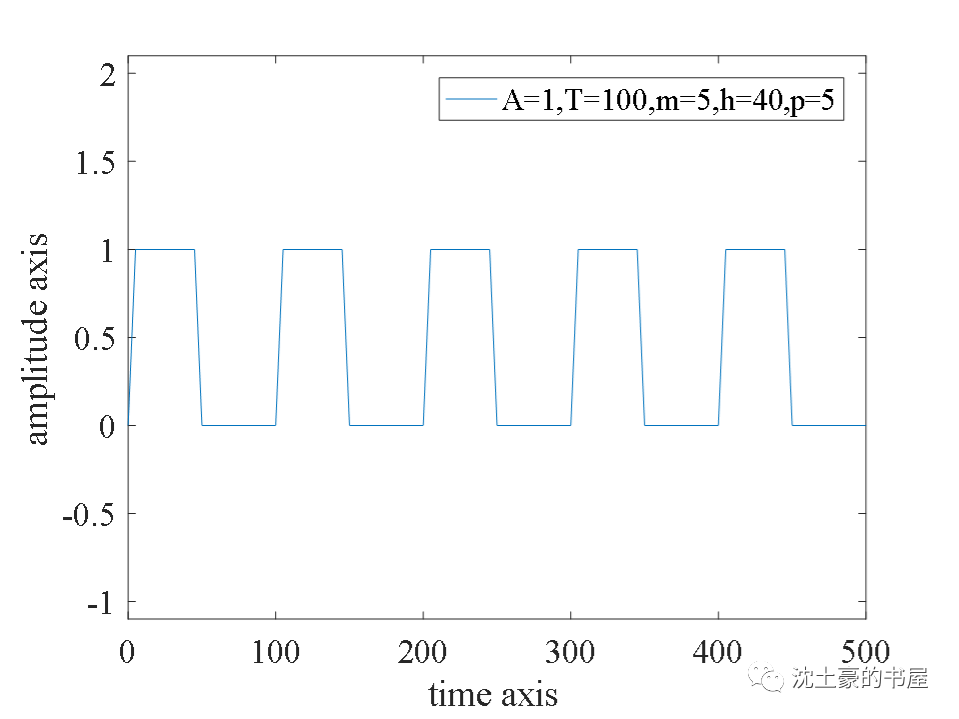
振幅A=2,周期T=150,上升时间m=20,正脉宽=50,下降时间p=1;
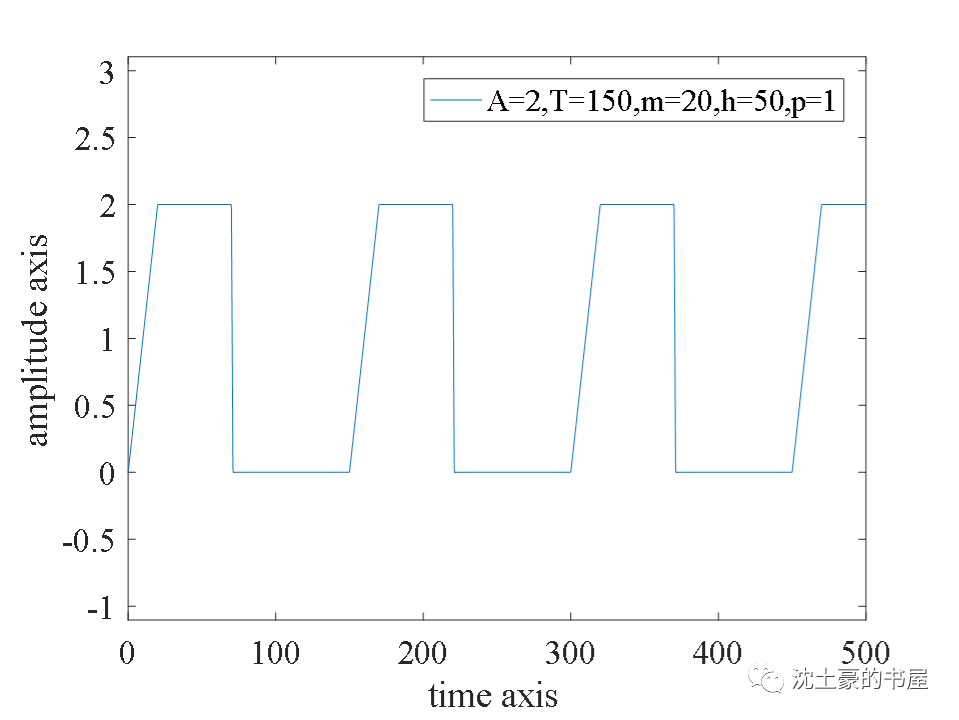
-
MATLAB仿真
+关注
关注
4文章
175浏览量
19888 -
傅里叶变换
+关注
关注
6文章
429浏览量
42534 -
矩形波
+关注
关注
0文章
12浏览量
10275
发布评论请先 登录
相关推荐
小波与傅里叶分析基础

傅里叶级数的数学推导公式

傅里叶级数的数学推导





 梯形波的傅里叶级数分解
梯形波的傅里叶级数分解
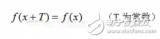










评论