作者:Chris Goodyer 2023年5月16日
广泛工作负载(包括许多基准测试,如SPEC)的性能依赖于基本数学例程的有效实现。这些例程可以通过矢量化和有效使用SIMD管道来利用性能。
最近的一篇博客文章(https://community.arm.com/arm-community-blogs/b/high-performance-computing-blog/posts/bringing-wrf-up-to-speed-with-arm-neoverse)描述了如何使用Arm Compiler for Linux(ACfL)和Arm performance Library(Arm PL)中提供的SVE子程序来提高Neoverse V1上天气预测模型的性能。
Arm优化的标量和向量数学例程实现在Arm软件/优化例程中作为开源软件公开提供(https://github.com/ARM-software/optimized-routines)。这些实现被方便地授权,允许用户在需要时直接将它们包含在其他项目中。此外,我们还将这些作为预编译二进制文件发布,称为Libamath,作为Arm PL和ACfL的一部分。
虽然ACfL能够通过自动矢量化生成对矢量数学例程的调用(请参见https://developer.arm.com/documentation/101458/latest/有关使用“-fsimdmath”编译器选项的更多详细信息,其他编译器可能还不允许在AArch64上发生这种情况。然而,将项目链接到Arm PL或在禁用自动矢量化的情况下使用ACfL构建它仍然可以访问矢量数学符号。Libamath随ACfL提供,但作为单独的库,因此可以通过添加-lamath将项目链接到Libamath。
在这篇文章中,我们强调了性能可能增加的规模,详细说明了精度要求,并详细解释了如何在自己的代码中直接使用这些函数。
准确性和性能
Libamath例程的最大错误低于4个ULP,并且仅支持默认的舍入模式(舍入到最近,绑定到偶数)。因此,与这些函数的其他矢量化实现类似,从libm切换到libamath会导致一系列例程的少量精度损失。
Neoverse V1系统的预期性能增益如以下2个单精度和双精度例程图所示。
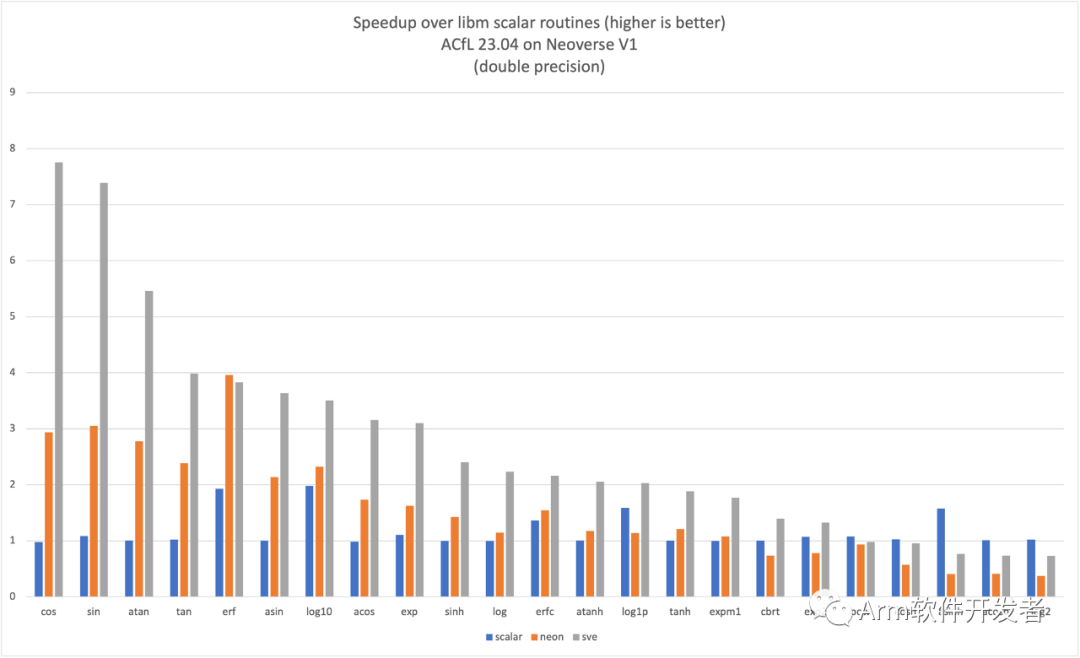

命名和调用约定
Libamath标量例程的名称与libm中使用的名称相匹配,例如,单精度和双精度指数分别称为expf和exp。
每个向量例程都在向量ABI名称下公开。AArch64的向量函数ABI(https://github.com/ARM-software/abi-aa/blob/2982a9f3b512a5bfdc9e3fea5d3b298f9165c36b/vfabia64/vfabia64.rst#451name-mangling-function)中定义的向量名称篡改与glibc的向量ABI(https://sourceware.org/glibc/wiki/libmvec?action=AttachFile&do=view&target=VectorABI.txt)匹配(第2.6节)。
例如,标量、Neon和SVE单精度指数的符号分别读作expf、_ZGVnN4v_expf和_ZGVsMxv_expf。
向量ABI 在向量ABI中,向量函数名被篡改为以下各项的串联:
'_ZGV' '_'
其中
• :标量libm函数的名称 • :Neon为“n”,SVE为“s”
• :“M”表示屏蔽/谓词版本,“N”表示无屏蔽。仅为SVE定义屏蔽例程,仅为Neon定义无屏蔽例程。
• :表示以车道数表示的矢量长度的整数。对于Neon,双精度中=‘2’,单精度中=‘4’。对于SVE,=‘x’。
• :对于1个输入浮点或整数参数,“v”用于签名,“vv”用于2个。有关更多详细信息,请参见AArch64的向量函数ABI(https://github.com/ARM-software/abi-aa/blob/2982a9f3b512a5bfdc9e3fea5d3b298f9165c36b/vfabia64/vfabia64.rst#451name-mangling-function)。
示例
从最新版本23.04开始,Arm Performance Libraries提供了文档和示例程序,以展示用户如何直接从其程序中调用矢量例程,而不依赖于自动矢量化。以下代码片段说明了如何调用Neon双精度sincos、SVE单精度pow和SVE双精度erf。
所有标量和向量例程的声明都在头文件amath.h中提供。
int main(void) {
// Neon cos and sin (using sincos)
float64x2_t vx = (float64x2_t){0.0, 0.5};
double vc[2], vs[2];
_ZGVnN2vl8l8_sincos(vx, vs, vc);
// SVE math routines
// single precision pow
svbool_t pg32 = svptrue_b32();
svfloat32_t svx = svdup_n_f32(2.0f);
svfloat32_t svy = svdup_n_f32(3.0f);
svfloat32_t svz = _ZGVsMxvv_powf(svx, svy, pg32);
// double precision error function
svbool_t pg64 = svptrue_b64();
svfloat64_t svw = svdup_n_f64(20.0);
svfloat64_t sve = _ZGVsMxv_erf(svw, svptrue_b64());
}
结论
使用Arm Compiler for Linux时,libamath通过依赖于编译器的自动矢量化,为这些应用程序提供了利用性能的潜力。这提供了所有math.h例程的Arm优化Neon和SVE变体。我们的“优化例程”(https://github.com/ARM-software/optimized-routines)开源代码库提供了对更广泛使用的例程的最新优化的访问权限。这些矢量化算法已经用于加速计算物理、机器学习和网络等各种应用程序中的基本数学运算。当使用这两种方法之一时,用户还可以使用上面描述的接口直接从其代码中调用这些矢量例程。
-
ARM
+关注
关注
134文章
9099浏览量
367748 -
SPEC
+关注
关注
0文章
31浏览量
15809 -
数学函数
+关注
关注
0文章
9浏览量
6357
原文标题:在Arm上使用向量数学函数
文章出处:【微信号:Arm软件开发者,微信公众号:Arm软件开发者】欢迎添加关注!文章转载请注明出处。
发布评论请先 登录
相关推荐
MATLAB常用的基本数学函数
XC32函数在向量x到大
学习DSP库的基本数学函数
基于支持向量机的预测函数控制
基于先验知识的支持向量机在图像分割中的应用
发掘函数级单指令多数据向量化的方法
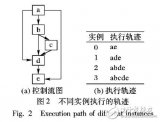
基于申威26010处理器的扩展函数库实现与优化
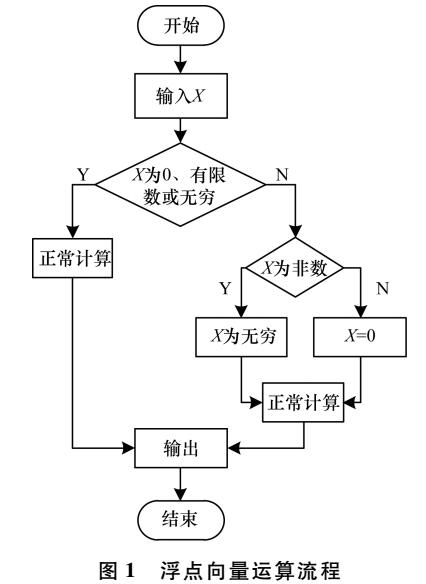
简单的数学运算计算数学函数的方法CORDIC的详细资料概述
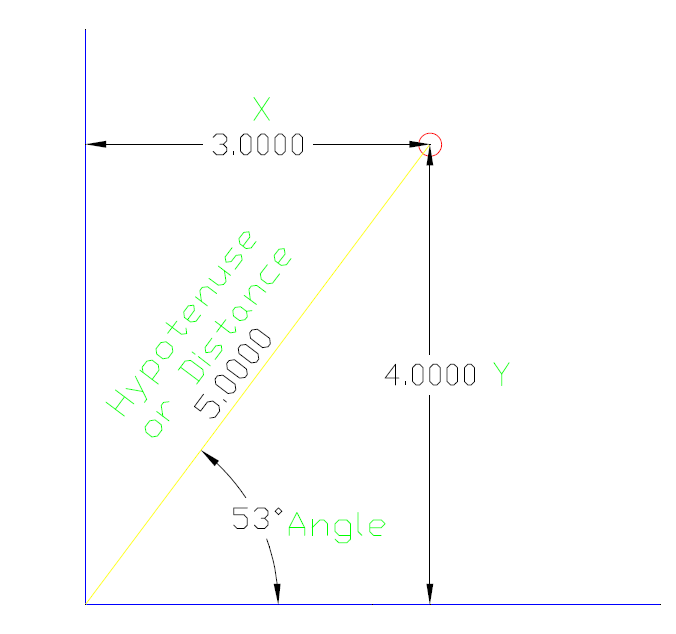
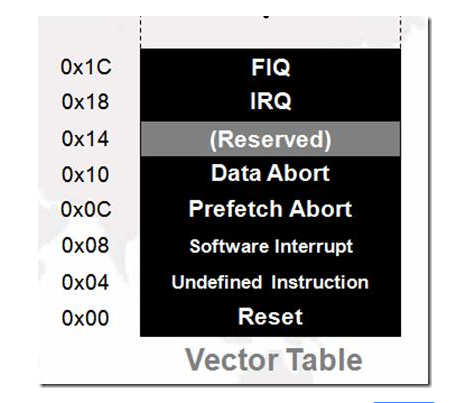
如何理解ARM异常、中断和向量表




 在Arm上使用向量数学函数
在Arm上使用向量数学函数











评论