如何阅读MTF曲线-电子发烧友网

前言

在一次关于如何阅读MTF曲线的网络讨论中，“光学规律太复杂而令人厌烦”，是一个公认的意见；可见，对于摄影师来说，理解数字的世界是那么的困难！

不过，情况并没有那么糟糕，我将在接下来的内容向你展示，其实你并不需要掌握傅里叶高等光学之类的，也可以理解那些基本关系。读完本文，你将能够从制造商或测试机构发布的MTF数据中判断镜头的特性。另外，我们还将介绍MTF的局限性，以便你可以批判地认识镜头评论。

一些人看到那么多公式曲线后，可能会说这些对于拍好照片并不是必需的，摄影更重要的是实践；但以一个更好的方式理解你的工具，不挺有意义吗？这也是我希望大家在阅读本文后能得到的，下面我也会借助一些图像向大家展示说明。

点扩散函数

当摄影师想拍一张逼真的图片时，他们希望有一个理想的镜头，该镜头会将从物品某一点反射出的光线再汇聚于对应图片上的一点。但实际的镜头只能达到部分的理想效果，而且现实中几何意义的像点并不存在。镜头像差、制造公差以及光的波动性等则导致来自物方点光源的光线总是分布在理想的像点的周围。

某种程度上，这片区域可能是最小的弥散圆：其中光线分布并不均匀，亮度从内到外逐渐减小，而且形状也很少是圆形的。这种效应被称为“点扩散函数”，其形状和大小表征透镜的图像质量。

如果将摄影比作“绘画”，则点扩散函数就是笔迹，即透镜的“笔触”，就像“笔迹”有宽、平、尖或硬的刷子，透镜同样有不同的类型的“笔迹”。

但是为什么不用它来定量描述图像质量呢？有以下3点原因：

首先，点扩散函数的形状有时非常复杂，不能使用简单数字描述。如下图所示，前六个扩散点图是中等图像质量的示例，也是全孔径高速镜头、广角镜头边缘或轻微散焦的典型情况。

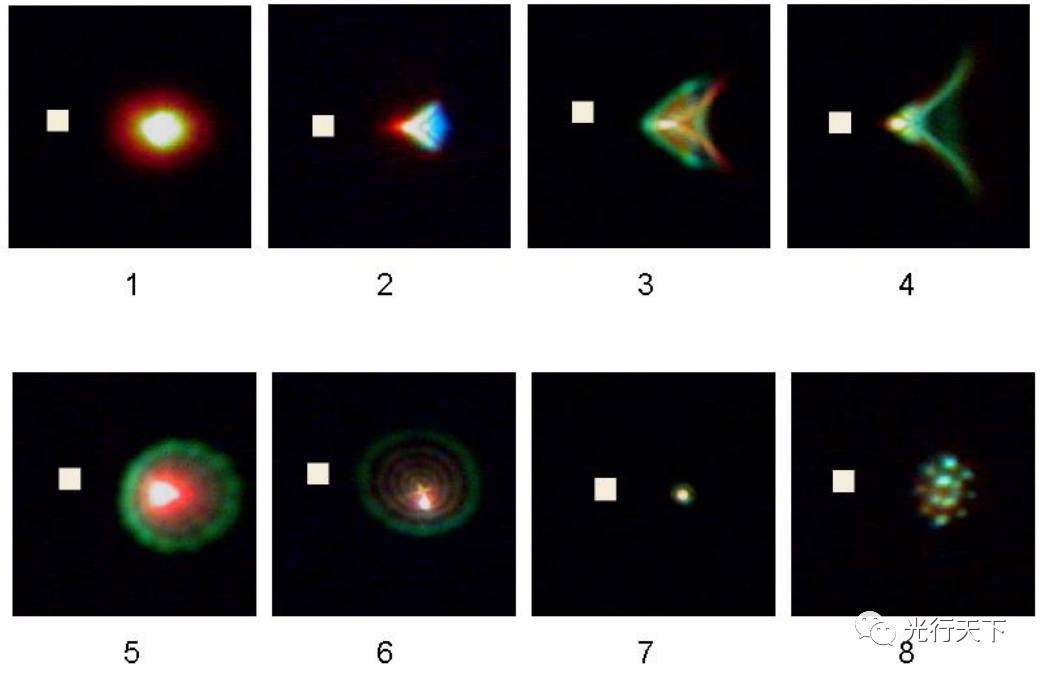
在1200万像素、30mm全画幅相机的以上每张图片上都贴了一个8.5微米的白色方块用于尺寸对比。所有这些扩散点都比这个方块大得多。

图7为优秀的图像性能的扩散点图，但在数字传感器上通常看不到如此小的扩散点。最右边的图8为加载了低通滤波器后的扩散点，低通滤波器放在传感器前用于抑制莫尔效应。而低通滤波器的几个双折射片放大了扩散点，导致图像质量被人为降低。

第二个原因是几乎没有这种单一、孤立的扩散点。例如：只有在漆黑的夜晚拍摄星星时，才能达到与实验室中相同的效果。绝大多数图片在相机中以复杂的方式生成，是大量单个扩散点的叠加。

因为物体的某一小块是由大量密集的点组成的，这些点对应于镜头后面图像中的许多密集的理想像点。由于实际的扩散点不可能无限小，因此实际上扩散点会相互交叠，即图像上一点的亮度是许多扩散点的二维积分。因此，笔触和我们所看的图像之间的数学关系并不是那么容易处理的。

第三个原因就是，我将要解释的方法可以更完美的描述从镜片到眼睛的整个图像链。 调制传递

由于我们主要关注物体是如何成像的，物体不同于星星，它包含无穷多个点，因此我们必须找到另一种定量描述图像质量的方法。我们使用正弦的亮度分布模型来研究一个尽可能简单的物体是如何成像的。正弦亮度分布模型是明暗交替的条纹，其中明暗条纹的过渡是渐变且连续的（即正弦变化），就像我们插座中的电力随时间的变化一样。

我们选择正弦变化的模型的原因是其图像同样是正弦函数变化的，无论其扩散点的形状有多复杂。它的一些其他特性也保持稳定或至少与成像质量无关：条纹的方向不会改变，频率（每单位长度的条纹数量）仅根据成像比例而变。

图像的明暗条纹之间的亮度与原始模型的不再相同，主要因为扩散点的延伸（衍射），即部分光落在完全黑暗的区域而不是对应的明亮位置。

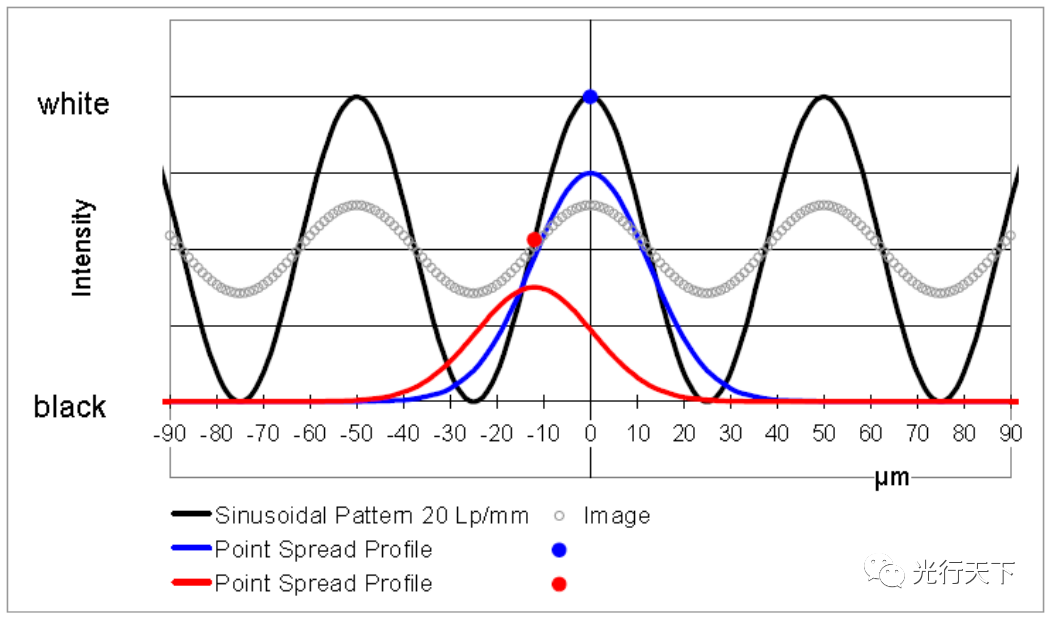上图黑色曲线显示了正弦条纹模型的强度分布（垂直于条纹的横截面）；其每1mm有20个周期，每个周期50微米；红色和蓝色为扩散点的中心横截面的亮度分布。蓝色曲线即正弦模型上蓝点的亮度在成像时分散到周围区域的图形，有一部分光落入蓝点旁边25微米的“黑暗山谷”。