昨天关于跨导Gm的结论还是有点粗糙,应该说跨导很复杂,和沟道的特性有关系;需要分开讨论,我们先试着了解导电沟道电流是怎么算的:

如图,电流分扩散电流和漂移电流,工作时的mosfet电流很大,主要是漂移电流,因此忽略掉扩散电流的成分。
同时我们讨论平面MOS,导电沟道主要是栅极下面薄薄的一层(y方向上),x方向上的电场我们也忽略掉。
最后我们得到,沟道中某截面的电流密度Jn和沟道迁移率μ,沟道中载流子浓度n,以及截面上此点的电势Φ有关。

上上图是求得电流密度 J,此图我们求电流,就是对电流密度做关于体积的积分,沟道y方向上的长度为L,沟道宽度为Z,最后得到电流ID(既是沟道电流也可以看成漏极电流)

这个Z有的文献里面也会写成W,这个公式表明,沟道电流Id大小与沟道宽长比W/L成正比,也和沟道内的电荷密度QN成正比,同时也是电势Φ从0到Vds(从源级到漏极)的积分。
现在要求这个积分,主要是求电荷密度QN,场效应管的QN不知道,我们可以通过MOS电容的电荷分布来近似。
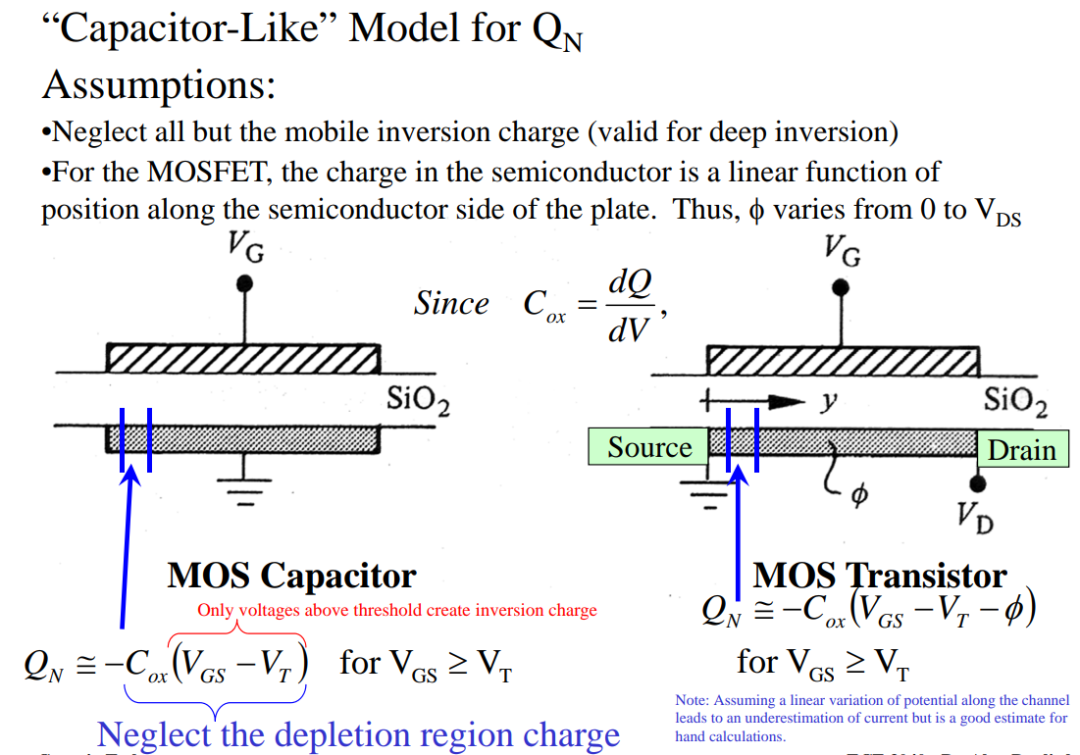
左边就是一个最简化的MOS电容模型,上极板接电压VG,中间的介电材料是SiO2,标准的平行板电容器。当VG值>阈值电压Vt,反型层建立,沟道的总电荷密度QN就是栅电容乘以电容两端的电势差。
那么对比一下,从MOS电容到MOS晶体管,无非就是加了源级D和漏极S,其中漏极S还是接地的,电压为0,所以,只加入了源级电压VD,那么,沟道从漏极到源级(D到S),无非是每个点的电势不一样,最小是0,最大是VD,仅此而已。
所以接下来就好办了,直接设沟道上某处的电势为Φ,那么此处的电荷密度QN和MOS电容计算方法一样,也是栅电容Cox乘以电势差(VG-Vt-Φ)
代入到上面电流ID的公式,
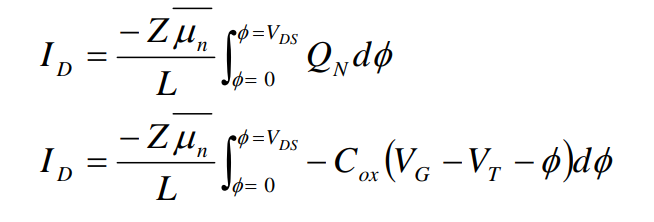
然后对沟道上的每个点的电势进行积分(积分下限是源极的0V,积分上限是漏极的VD),把电势看成变量,其余为常量,被积函数是最简单的一次方程,那么原函数就是二次方程;

这个方程就是上篇文章的萨支唐方程,描述了MOSFET的输出电流与栅极电压,漏极电压的关系。
需要注意的是,这个方程使用条件有两个,首先是要MOS沟道完全开启,也就是VGS要大于阈值电压Vt,其次沟道不能夹断,也就是VDS要小于VDsat(预夹断电压/饱和电压)。
这个夹断点的电压怎么计算?看图
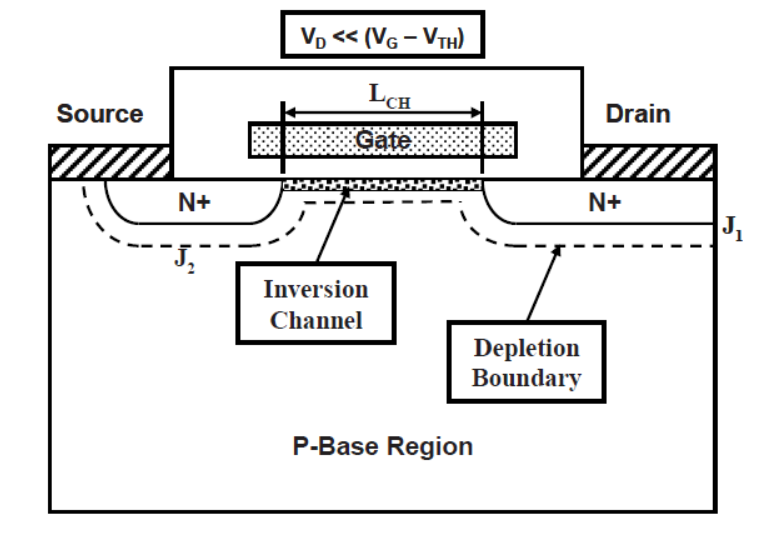
分4种类型讨论;
1: 沟道开启,漏极电压VDS远小于栅极电压和阈值电压的差值VG-Vth,此时二阶量直接忽略:
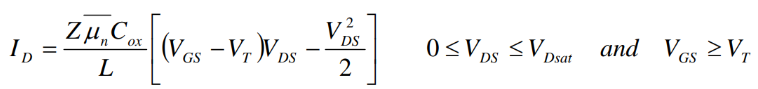
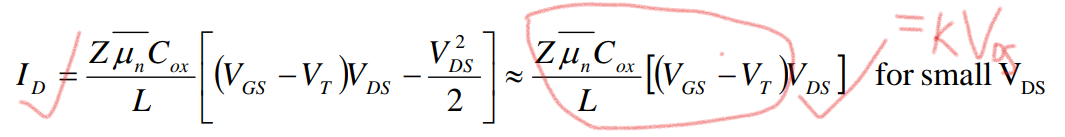
得到ID和VDS线性相关,对应的就是MOSFET输出特性曲线的线性区:
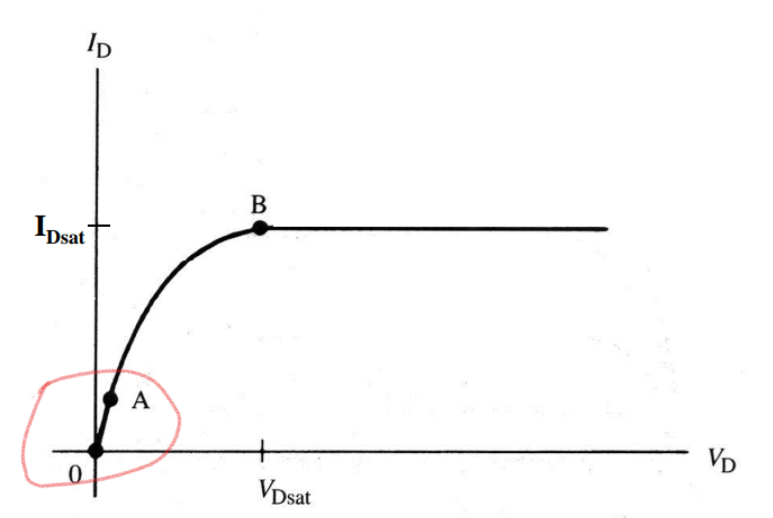
对应的是输出特性曲线上0-A这一段直线。
2: 沟道开启,漏极电压VDS增大,依然不大于栅压和阈值电压之差VGS-Vth。那么此时沟道内由于右边电势为VDS,左边VS=0,必然会出现沟道右边电势高,左边电势低的情况,那么,沟道右边的反型层处电势=VGS-Vth-VDS,会变小,最右边栅极的影响力被漏极抵消一部分,一部分本来可以栅吸引形成沟道的电子,就被漏极正电压拉过去了,右边的反型层便逐渐减弱,沟道在靠近右边漏极区域慢慢变窄,于是电流能力变得没那么强。
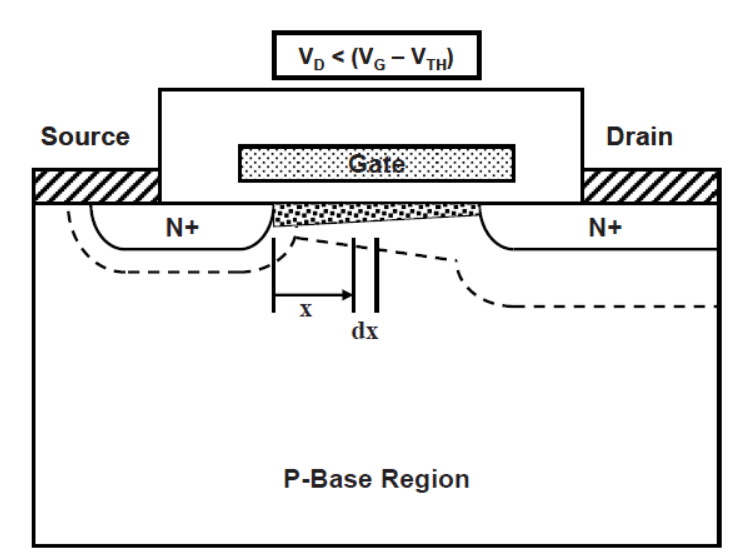
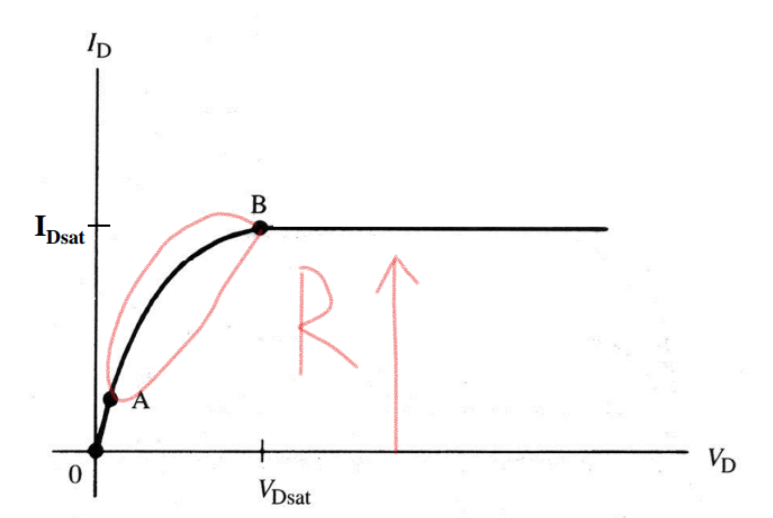
反应在输出特性曲线上就是电流上升速度变慢,导通阻抗变大:A到B这一段
3: 预夹断点(pinch-off),当电流继续上升,漏极电压VDS持续增大,达到VDS=VGS-Vth这个点时,此时沟道的最右边终于顶不住了,由于VGS-Vth电势没有VDS高,这里已经没有反型层了,也就是导电沟道在这里开始消失了。
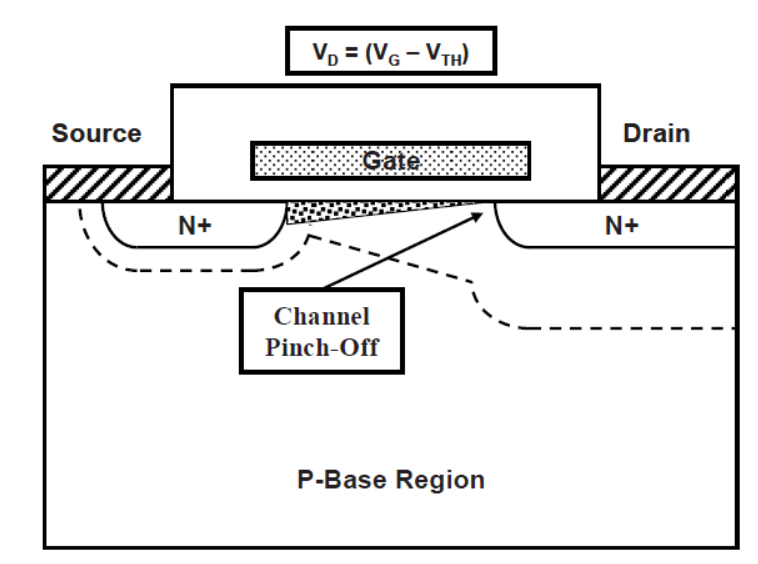
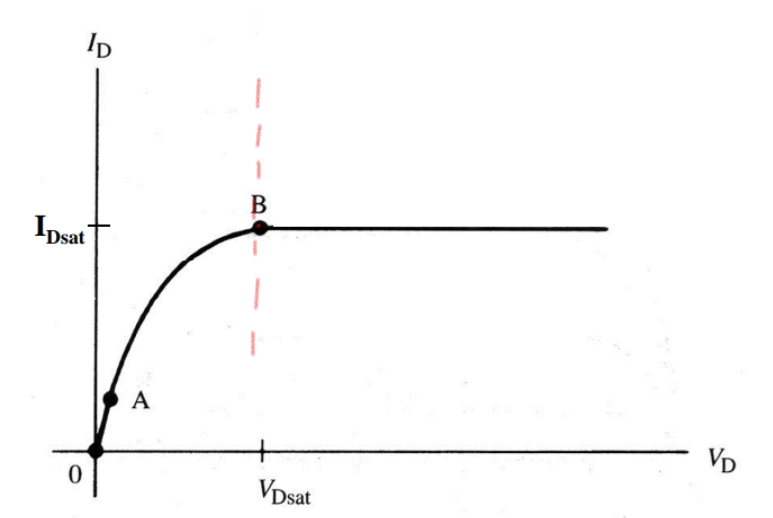
反映在输出特性曲线上就是漏极电流饱和了,再也无法靠提升VDS来提升了,除非提升栅压,否则电流是无法上升的。
4: 完全夹断(饱和区)
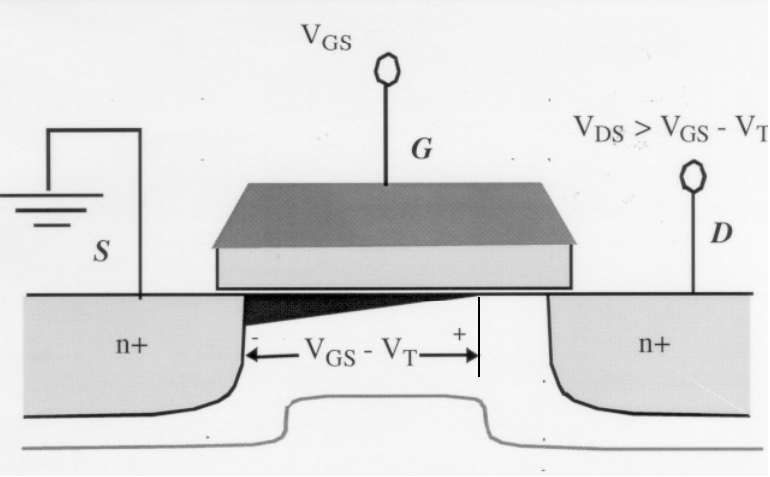
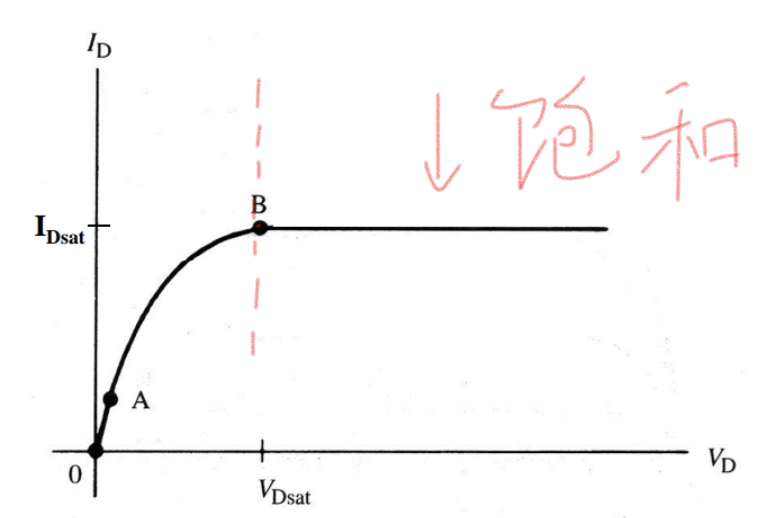
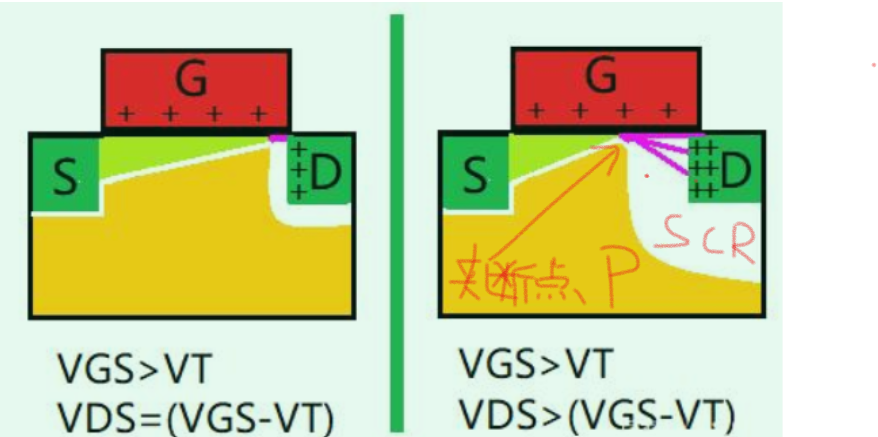
沟道完全夹断之后,源级到漏极之间的导电沟道断了一部分,也就是说电子只能沿着沟道跑到中间,然后沟道不见了,不过为什么还是有电流呢?
因为夹断点后面支撑它的不是原来的黄色P型区域,而是电压升高更吸引电子的漏极D及其空间电荷区(白色SCR) 。因此电子冲入空间电荷区,就相当于几乎没有阻挡的准自由电子快速被漏极收集。所以虽然沟道夹断了,但是电流依然还在。
-
电容器
+关注
关注
64文章
6215浏览量
99516 -
MOSFET
+关注
关注
146文章
7149浏览量
213081 -
场效应管
+关注
关注
46文章
1162浏览量
63902 -
MOS管
+关注
关注
108文章
2408浏览量
66744 -
VDS
+关注
关注
0文章
45浏览量
10723
发布评论请先 登录
相关推荐
解答74HC14中正向阈值电压和负向阈值电压是什么/电压为多少
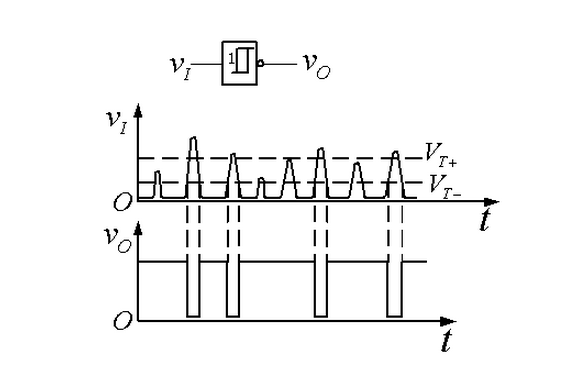
MOS管阈值电压的问题
迟滞比较器阈值电压除了由我的电阻参数设定还要其他因素吗?
阈值电压的计算

MOS管阈值电压与沟长和沟宽的关系
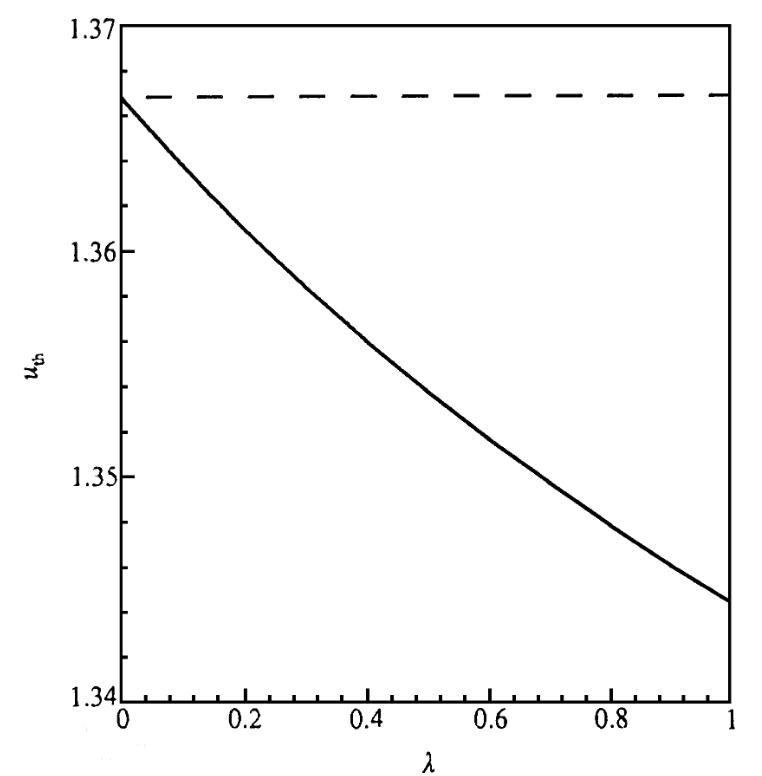
GaN基MIS-HEMTs阈值电压漂移的快速动力学论文免费下载
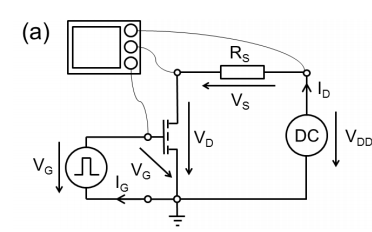
如何突破EDA封锁 卷起来的阈值电压
不同Vt cell工艺是怎么实现的?阈值电压和哪些因素有关系?
影响MOSFET阈值电压的因素
什么是MOS管亚阈值电压?MOSFET中的阈值电压是如何产生的?
MOSFET阈值电压是什么?影响MOSFET阈值电压的因素有哪些?
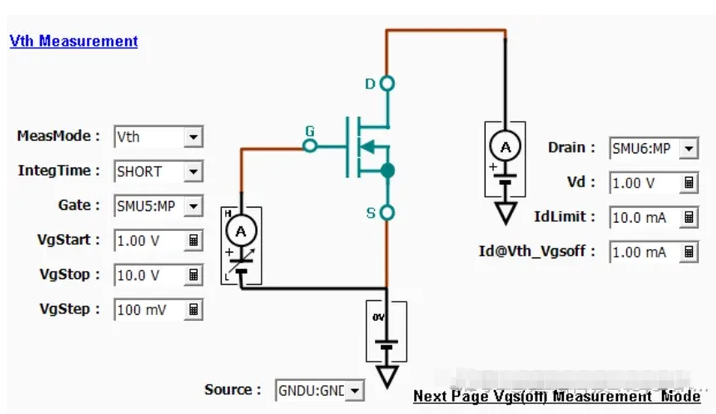




 沟道反型层阈值电压Vth介绍
沟道反型层阈值电压Vth介绍










评论