硬件加法器怎么利用基础门电路进行加法计算呢？

我们现在知道，「通电」代表「真」，用逻辑1表示；「不通电」代表「假」，用逻辑0表示。「与门」电路是用晶体管搭建的，符号长这样：

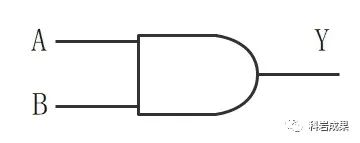
A与B的通断，可以决定Y点是否通电。

我们还为A、B与Y之间的关系画了一张表（真值表）：

接着我们设计出了简单的「或门」「非门」，用它们可以搭建各式各样其他的门电路。

这篇文章讲一下，怎么利用基础门电路进行加法计算。

二进制加法

我已经忘了是什么时候学的加法了，应该是小学吧，先学10以内的，再学100以内的，然后不管多大的数都可以随便加了，算式很简单，就是逢10进1。

下面这个式子是一个万以内的加法：

相应的，二进制就是逢2进1，下面这个式子是2个8位二进制数的加法计算：

半加器

8位二进制数还太复杂，我们先来看看1位二进制数怎么计算的，一共有以下4种情况：

观察一下就能发现2个规律。

第一个规律，只考虑加法，不考虑进位时，加数与和之间的关系如下：

相同为0，不同为1。这个关系和「异或门」是相同的：

异或门我们之前没有聊到过，电路图长这样：

第二个规律是，如果只考虑进位，不考虑加法，加数与进位之间的关系如下：

只有全1时，才为1。发现了吗，这和本文开头与门的真值表是一样的。

2个一位二进制数相加将产生一个加法位和一个进位位，加法位输入与输出的关系跟与门是一样的，进位位跟异或门相同。

所以，可以像这样把两个门电路连起来，计算2个二进制数（A和B）的和：

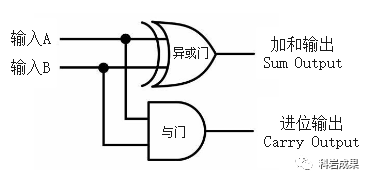
我们称这个电路为「半加器」，因为它只能计算2个一位二进制数的加法，没有办法将前面加法可能产生的进位纳入下一次计算中，如果有进位则实际上是需要3个加数参与计算。

用门电路画太复杂，可以封装起来这样表示半加器：

全加器

怎样计算3个加数的二进制加法呢？需要将2个半加器和一个或门如图连接起来：

左边能看到它有3个输入，右边依旧是1位加和输出，1位进位输出。

2个数的加和与上一次的进位相加，得出的加和作为3个数最终的加和；2个数相加或3个数相加的进位作为3个数加和最终的进位位。

用文字描述有点不好理解，把这个电路图全部输入和输出情况都展示出来，画一个表就明白了：

很明显，这个表就是2个一位二进制数带进位的全部状态。

每次做加法时画2个半加器和一个或门很麻烦，我们用下面这个图示把它们封装起来，这个能计算3位二进制数加法的电路就称为「全加器」。

加法器

现在回到开头那个二进制加法：

它有8个二进制位，到目前为止我们还只能计算2个一位二进制数，最多再增加一个进位的加法，我们最终的目标当然是2个8位、16位乃至32位数的加法。

其实，非常简单，用8个全加器一块算！

把8个全加器每个进位输出作为下一个的进位输入，首尾相连就可以啦！

每次这样画太麻烦，可以封装成一个框图：

大箭头代表8个输入/输出端，有8个独立的信号。

一旦我们拥有了8位二进制加法器，把它们级联起来，很容易就能得到一个16位或32位的加法器啦。

end

加法计算是计算机的基本运算，其实，计算机唯一的工作就是做加法计算。 不论是减法、乘法、除法、在线支付、火箭升空还是AI下棋，都是利用加法实现的。

把加减乘除和逻辑运算等运算单元集成起来，就组成了CPU中的基本计算单元：ALU（算术逻辑单元Arithmetic and Logic Unit）。

用加法器计算2个数的加法其实就是用硬件方式实现了一个加法计算器，输入A和输入B的高低电平决定了输出S和CO的高低电平。

这样的电路同一时刻只能表示一种状态，只要改变了A、B中任意一位，输出就会有所变化。

现在我们想计算更多二进制数的加法，比如5个数A、B、C、D、E的加法（先不考虑进位）。

步骤应该是这样：首先把A、B作为输入，得出一个输出S1，我们要记下来S1的值，然后把S1和C作为输入，得出S2....以此类推，要记下很多个数，然后再用加法器计算。

5个数都已经很麻烦了，如果要计算更多个数该怎么办？能不能把每次计算完的结果存起来，下次继续使用呢？