光伏组件仿真模型、半物理模型与数学模型构建及示例

组件输出仿真模型可以通过半物理模型或数学模型实现，根据应用场景的不同可以选择不同模型观察和研究组件特性。例如半物理模型相对比较直观适合用于研究单块组件在不同外部条件下其输出变化，而在大规模系统仿真中则数学模型比较适用了。

以下分别对半物理模型和数学模型进行介绍，按照这些年的实际工作中遇到的问题这两个模型基本能够覆盖应用分析的目的了。

光伏组件半物理模型

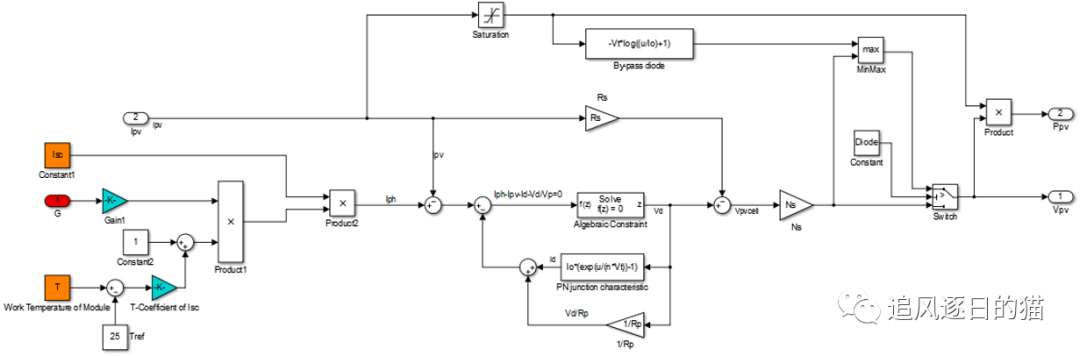
根据在电池模型中介绍的二极管模型，可用Simulink搭建出光伏组件仿真模型，例如下图所示构建的一个子系统。下图模型中的下半部分是光伏组件的主要部分，下面的‘Id’是中间的二极管的PN节特性，‘Rp’是并联电阻，‘Rs’是串联电阻，输出的太阳电池板的开路电压。

模型的上半部分是模拟了旁路二极管部分，‘By-pass diode’是一个二极管，选择器可选择是否加载旁路二极管，通过‘Diode’和‘Switch’部分的添加来确定。

将上述子模块‘封装’并进行‘并联’，如下图由三个子系统（分别代表实际组件中有一组二极管管理的电池串）构成一个组件系统，即可建立一块组件的仿真模型，研究实际组件在不同工况下的输出特征。

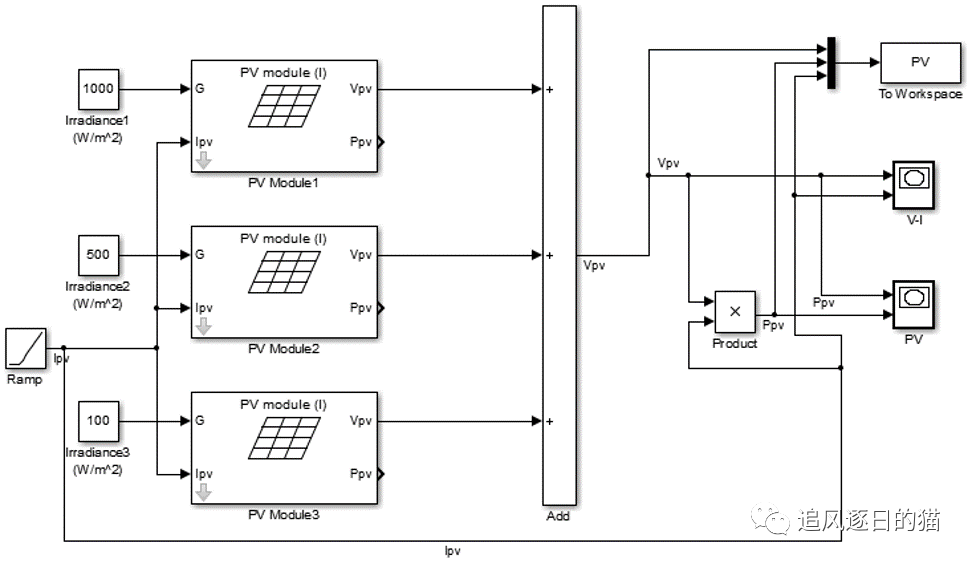
案例分析，现实环境中，树荫、供电电缆、云块、甚至是鸟类排泄物等都会造成太阳能光伏板部分被遮挡，而遮挡现象会对光伏系统造成很大影响。通过上图模型模拟光伏组件部分阻挡条件下的输出特性。

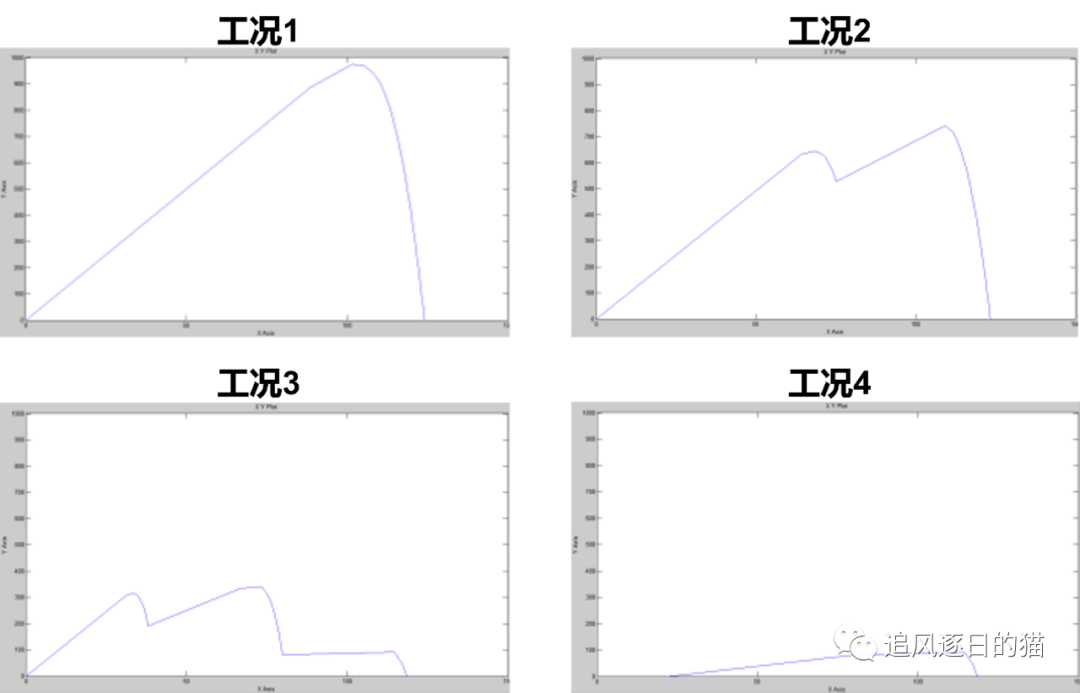
分别分析4种设定工况下组件的输出曲线：

工况1.无遮挡模式，光照强度为1000W/m2；

工况2.遮挡且有旁路二极管模式，光照分别为1000、1000、700W/m2；

工况3.遮挡且有旁路二极管模式，光照分别为1000、500、100W/m2；

工况4.遮挡且没有旁路二极管模式，光照分别为1000、500、100W/m2；

仿真结果如下，其中IV曲线中最大功率点即为理论上在相应工况下光伏组件能输出的最大功率。

光伏组件数学模型

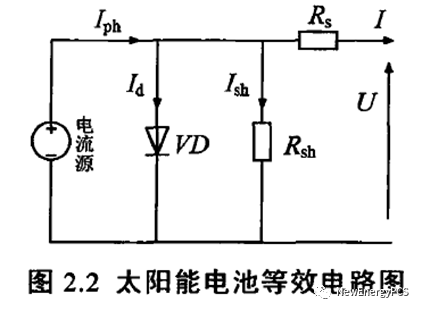
光伏组件外特性曲线可以通过等效二极管模型的数学模型进行仿真，即下式表述方程

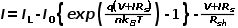
k B ，波尔兹曼常数，1.380649×10^-23^J/K；

n，光伏组件等效理想因子，通常设定1~2之间的值；

I L ，光生电流，其为辐照度与温度的函数：

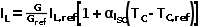
G ref =1000W/m2；T C,ref =298K；

G，光伏组件受到的实际辐照；

α Isc ，光伏组件电流温度系数；

T c ，光伏组件工作温度；

I 0 ，光伏组件等效反向饱和电流，除本身器件特性外I0主要受温度影响：

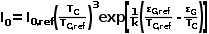
I 0,ref ，298K标准温度下组件的等效反向饱和电流，其可以通过标准温度下光伏组件Voc、Isc及Rsh等参数通过下式获得：

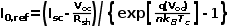
εG,ref及ε G ，材料在298K或Tc温度下的能带宽度，单位为焦耳J（1eV=(1.60217733±0.000000 49)×10^-19^J）；

硅材料约为1.12eV，对于硅由于晶格的热膨胀，禁带宽度Eg随温度的增加而减小，其与温度的关系在SPICE中计算方程为

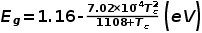
Rs，光伏组件等效串联电阻，其为辐照度与温度的函数：

辐照度/温度对串联等效电阻Rs影响

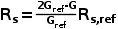
R s,ref ，298K标准温度下组件的等效串联电阻；

Rsh，光伏组件等效并联电阻，其为辐照度与温度的函数：

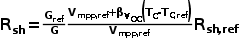
V mpp,ref ，298K标准温度下组件最大功率点电压；

β Voc ，光伏组件电压温度系数；

R sh,ref ，298K标准温度下组件的等效并联电阻；

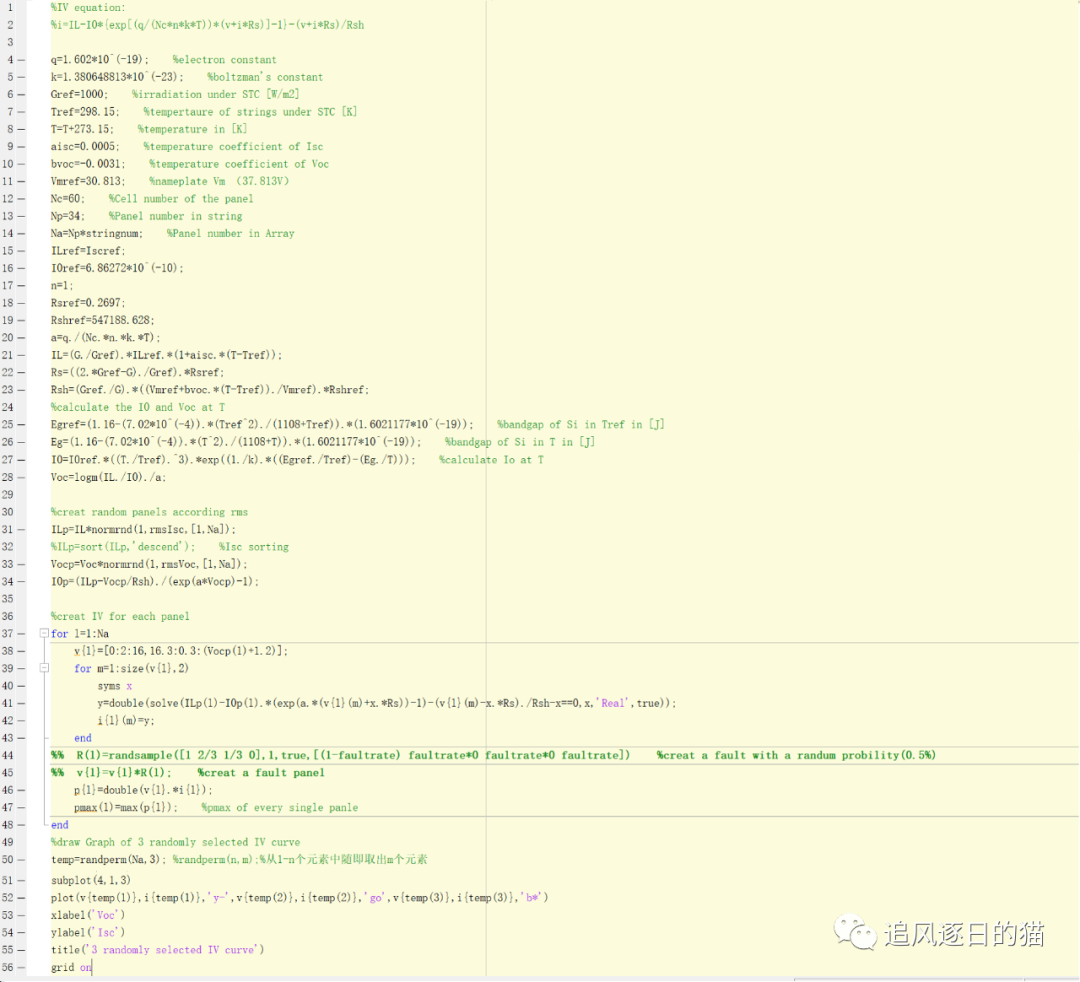
以下是利用上述数学模型按照特定分布规律随机生成大量光伏组件电性能输出曲线的MATLAB程序演示：