SVPWM概念介绍
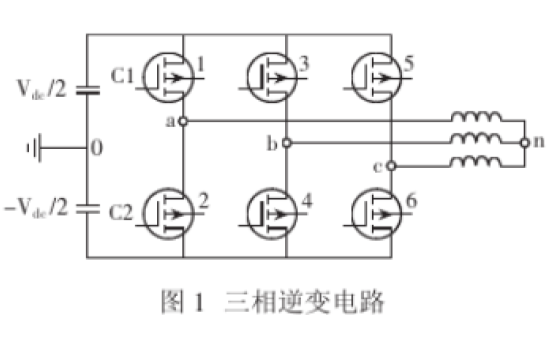
SVPWM一般用于逆变器,交-直-交变频器等场合,可以理解为一种开关触发顺序与脉宽大小的组合,类似与PWM的面积等效原理,只不过,利用这种开关触发顺序和组合可以在定子线圈中产生三相互差120电角度,失真较小的正弦电流波形,使电机获得圆形磁链轨迹。三相逆变电路如图1所示。
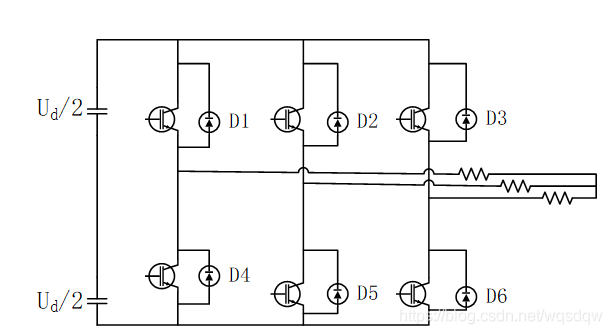
图1 三相逆变电路
三相逆变电路可以从左往右可以分为三个桥臂,每个桥臂又分为上下两个桥臂,上桥臂导通用“1”表示,下桥臂导通用“0”表示,则输出的电压矢量可以又三位二进制数表示,即000-111,其中,000和111这两种导通情况下,输出的电压为0,因此除去这两种电压,还存在着六种电压矢量,这六个电压矢量正好分成一个六边形的区域,如图2所示。
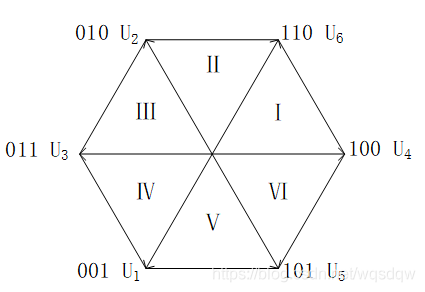
图2 SVPWM的六边形扇区
2.3/2变换
众所周知,在交流电机的三相绕组中流过三相电流,从而产生合成的旋转磁动势,它在空间上呈正弦分布,以一定的角速度顺着A-B-C相序旋转。而在计算时,我们如果采用三相坐标系去计算旋转磁动势的话,会比较复杂,因此,就需要寻找一种可以替代的计算手段。由于只要保证旋转磁动势与三相坐标系的旋转磁动势一致,而我们知道,单相、两相、三相都可以产生旋转磁动势,当然,以两相的最为简单。为此,三相的坐标系可以由两相正交坐标系替代和等效,等效的原则就是旋转磁动势相等。这就是3/2变换的由来。三相坐标系和两相正交坐标系如图3所示。
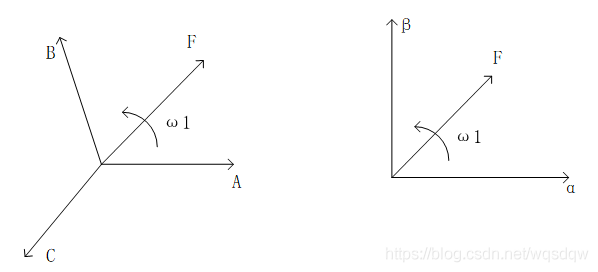
图3 三相坐标系(左)和两相坐标系(右)
下面介绍3/2变换的公式推导。由上述介绍可知,3/2变换就是三相绕组坐标系和两相正交坐标系之间的变换,二者变换等效的依据时磁动势矢量相等,因此,首先绘制出两个坐标系和磁动势矢量。将两个坐标系原点重合且A轴与α轴重合,并标上相应角度。按照磁动势矢量的等效原则,三相绕组坐标系合成的磁动势矢量在α轴和β轴上的投影与两相坐标系下合成的磁动势矢量在α轴和β轴上的投影均相等,如图4所示。
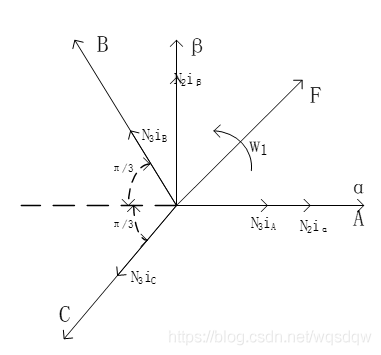
图4 三相坐标系和两相坐标系下的磁链矢量关系图
根据这个关系,列写出两个方程,即:
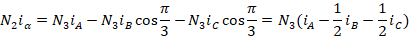
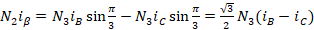
写成矩阵的形式有:
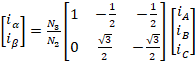
;按照变换前后总功率不变的原则,有
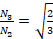
。至于这个值的推导过程,可以看图5所示。

图5 匝数比的推导过程
以上介绍的就是3/2变换。在SIMULINK仿真中,由3/2变换得到的Uα和Uβ
如下图所示,其中输入电压幅值为220V,频率为25Hz。
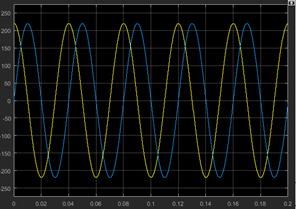
图6 Uα和Uβ输出的结果图
3.判断扇区
SVPWM的调制的第一步就是判断扇区,一般采用的方法使定义三个变量 Uref1 、 Uref2 、 Uref3 ,通过这三个参考变量的大小来判断扇区,他们的计算公式如下:
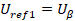
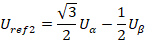
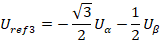
要理解参考变量与扇区值的关系,首先,绘制六边形扇形图以及U α 、 Uβ及三个参考变量的矢量图。如下图所示,举个例子说明,当合成电压矢量在扇区Ⅰ时,电压矢量在Uref1和Uref2上的投影为正数,电压矢量在Uref3上的投影为负数,以此类推,假设以A、B、C三个数来分别代表 Uref1 、 Uref2 、Uref3的正负值,参考变量为正,相应的数为1,参考变量为负,相应的数为0,且定义一个叫做扇区值N的变量,N=A+2B+4C,最终得出扇区值N与扇区的关系如表1所示。(注意:扇区值和扇区两者的概念要区分开来)
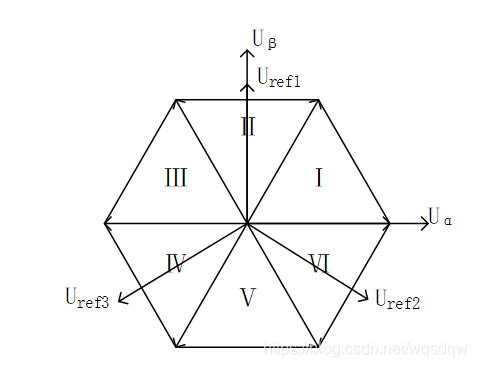
图7 参考变量矢量图
表1:扇区值N与扇区的对应关系
| 扇区 | Ⅱ | Ⅵ | Ⅰ | Ⅳ | Ⅲ | Ⅴ |
| 扇区值N | 1 | 2 | 3 | 4 | 5 | 6 |
|---|
4.计算跟SVPWM有关的时间量
首先,以扇区Ⅰ为一个简单的例子来分别计算出扇区相邻两边电压矢量的作用时间,在扇区Ⅰ中任意画一条合成的电压矢量,如下图所示,

图8 矢量作用时间举例
由面积等效原理,合成电压矢量在相邻两电压矢量的投影与作用时间的乘积要分别相等,根据这个求出相邻两电压矢量的作用时间及零矢量的作用时间,即:
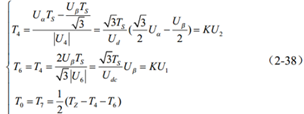
其中,K为比例系数,其值固定,为
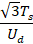
。
上述方法是常用的一种计算各扇区相邻电压矢量作用时间的方法,其基本原理是充分运用了U α 、 Uβ来简化计算,接下来介绍一种利用前面的三个参考变量 Uref1 、 Uref2 、Uref3来计算相邻电压矢量作用时间的方法,也是仿真过程中用到的方法,仿真结果表示这种方法也可以完成相同的效果。
首先,要用到上述的比例系数K,用K乘上 Uref1 ,用-K乘上 Uref2 、 Uref3 ,得到如下结果:
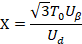

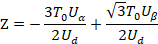
然后,得出对应扇区值和相邻两电压矢量作用时间的关系,如下表:
| t1 | Z | Y | -Z | -X | X | -Y |
| t2 | Y | -X | X | Z | -Y | -Z |
| t0 |
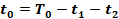 |
|||||
| N(扇区值) | 1 | 2 | 3 | 4 | 5 | 6 |
|---|
当然,这里t1和t2之和大于T0时,要进行相应的调制处理,否则会导致失真。调制的原理就是将t1和t2分别乘上
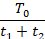
。
确定了上述扇区值与相邻两电压矢量作用时间的关系,接下来就要确定扇区的矢量切换点,也可以是通常说的占空比的概念。以七步法为例,何为七步法,就是将一个周期T0
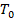
或Ts

(上述的相应说明里这两个时间可以认为是一个,只不过抄教材的时候没改哈哈)分成七个部分,每个部分对应一个时间。要利用七步法,首先还需要计算出矢量切换点的时间值,即:

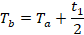
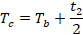
然后还是以扇区Ⅰ为例,处于该扇区时利用七步法得出的结果如下图所示。跟前面的六边形扇区相结合理解,桥臂1的上桥臂导通,另外两个桥臂的下桥臂导通时,输出的就是 U4 ,对应的也是100,同理U6对应的正好也是110,它两作用的时间也正好分别是t1和t2。利用七步法的好处就是使得这种输出对称起来,利于控制。
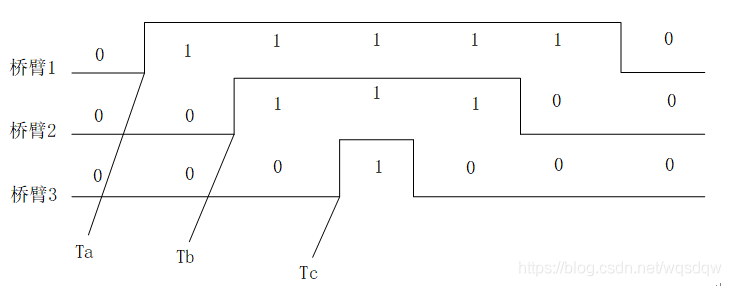
图9 扇区Ⅰ对应的七步法举例图
以上仅是针对一个扇区而言,接下来列出三项电压开关切换点Tcmp1,Tcmp2,Tcmp3与各扇区之间的关系。
| Tcmp1 | Tb | Ta | Ta | Tc | Tc | Tb |
| Tcmp2 | Ta | Tc | Tb | Tb | Ta | Tc |
| Tcmp3 | Tc | Tb | Tc | Ta | Tb | Ta |
| N(扇区值) | 1 | 2 | 3 | 4 | 5 | 6 |
|---|
再以扇区Ⅱ为例加深一下理解,如下图所示,扇区Ⅱ对应的扇区值为1,所以桥臂1,2,3的开关切换时间分别是Tb,Ta,Tc。由下图可知,U6和U2的作用时间也正好是t1和t2
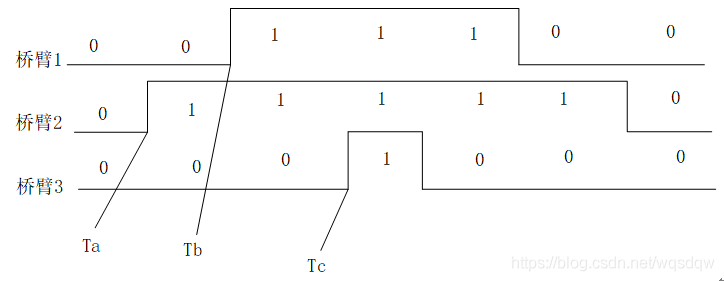
由Simulink仿真结果输出的三相电压开关时间切换点的波形如下图所示。

图10 三相电压开关时间切换点波形
5.PWM信号输出
将三相电压开关时间切换点与调制波进行比较输出SVPWM信号。仿真图和最终的输出结果如下面这些图所示。
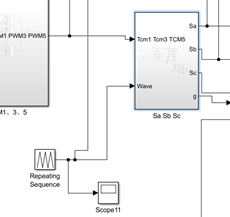
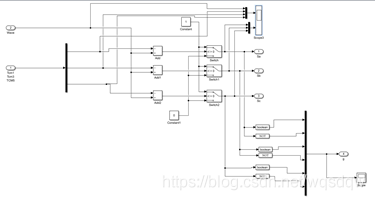
图11 三相电压开关时间切换点与三角调制波比较图
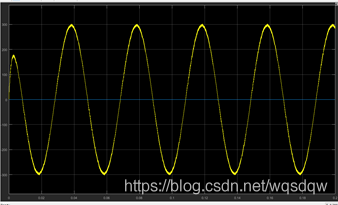
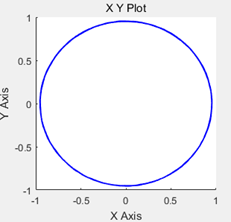
图12 输出的正弦线电压和圆形磁链图
-
PWM
+关注
关注
114文章
5124浏览量
213287 -
逆变器
+关注
关注
283文章
4671浏览量
206127 -
Simulink
+关注
关注
22文章
522浏览量
62274 -
SVPWM
+关注
关注
14文章
614浏览量
90570 -
仿真分析
+关注
关注
3文章
104浏览量
33627
发布评论请先 登录
相关推荐
Simulink系列免费教程(四)- Simulink建模及仿真参数设置介绍
simulink电机仿真学习 - SVPWM原理分析及仿真分析相关资料分享
simulink中关于电机矢量控制中SVPWM仿真
通过Matlab/Simulink对SVPWM控制算法进行仿真分析
如何使用SIMULINK对SVPWM算法进行仿真
SVPWM逆变器Simulink仿真





 SVPWM概念介绍与Simulink仿真分析
SVPWM概念介绍与Simulink仿真分析











评论