PyTorch教程-3.4. 从头开始执行线性回归

我们现在准备好通过线性回归的全功能实现来工作。在本节中，我们将从头开始实现整个方法，包括（i）模型；(ii) 损失函数；(iii) 小批量随机梯度下降优化器；(iv) 将所有这些部分拼接在一起的训练功能。最后，我们将运行3.3 节中的合成数据生成器 并将我们的模型应用于生成的数据集。虽然现代深度学习框架几乎可以自动执行所有这些工作，但从头开始实施是确保您真正了解自己在做什么的唯一方法。此外，当需要自定义模型、定义我们自己的层或损失函数时，了解引擎盖下的工作原理将很方便。在本节中，我们将仅依赖张量和自动微分。稍后，我们将介绍一个更简洁的实现，利用深度学习框架的花哨功能，同时保留以下结构。

%matplotlib inline
import torch
from d2l import torch as d2l

%matplotlib inline
from mxnet import autograd, np, npx
from d2l import mxnet as d2l

npx.set_np()

%matplotlib inline
import jax
import optax
from flax import linen as nn
from jax import numpy as jnp
from d2l import jax as d2l

No GPU/TPU found, falling back to CPU. (Set TF_CPP_MIN_LOG_LEVEL=0 and rerun for more info.)

%matplotlib inline
import tensorflow as tf
from d2l import tensorflow as d2l

3.4.1. 定义模型

在我们开始通过小批量 SGD 优化模型参数之前，我们首先需要有一些参数。在下文中，我们通过从均值为 0 且标准差为 0.01 的正态分布中抽取随机数来初始化权重。幻数 0.01 在实践中通常效果很好，但您可以通过参数指定不同的值sigma。此外，我们将偏差设置为 0。注意，对于面向对象的设计，我们将代码添加到__init__子类的方法中（在3.2.2 节d2l.Module中介绍 ）。

class LinearRegressionScratch(d2l.Module): #@save
  """The linear regression model implemented from scratch."""
  def __init__(self, num_inputs, lr, sigma=0.01):
    super().__init__()
    self.save_hyperparameters()
    self.w = torch.normal(0, sigma, (num_inputs, 1), requires_grad=True)
    self.b = torch.zeros(1, requires_grad=True)

class LinearRegressionScratch(d2l.Module): #@save
  """The linear regression model implemented from scratch."""
  def __init__(self, num_inputs, lr, sigma=0.01):
    super().__init__()
    self.save_hyperparameters()
    self.w = np.random.normal(0, sigma, (num_inputs, 1))
    self.b = np.zeros(1)
    self.w.attach_grad()
    self.b.attach_grad()

class LinearRegressionScratch(d2l.Module): #@save
  """The linear regression model implemented from scratch."""
  num_inputs: int
  lr: float
  sigma: float = 0.01

  def setup(self):
    self.w = self.param('w', nn.initializers.normal(self.sigma),
              (self.num_inputs, 1))
    self.b = self.param('b', nn.initializers.zeros, (1))

class LinearRegressionScratch(d2l.Module): #@save
  """The linear regression model implemented from scratch."""
  def __init__(self, num_inputs, lr, sigma=0.01):
    super().__init__()
    self.save_hyperparameters()
    w = tf.random.normal((num_inputs, 1), mean=0, stddev=0.01)
    b = tf.zeros(1)
    self.w = tf.Variable(w, trainable=True)
    self.b = tf.Variable(b, trainable=True)

接下来，我们必须定义我们的模型，将其输入和参数与其输出相关联。在(3.1.4)中使用相同的符号，对于我们的线性模型，我们简单地采用输入特征的矩阵向量乘积X和模型权重w，并加上偏移量b每个例子。Xw是一个向量并且b是一个标量。由于广播机制（参见 第 2.1.4 节），当我们添加一个向量和一个标量时，标量将添加到向量的每个分量。生成的 方法 通过（在第 3.2.1 节中介绍 ）forward在类中注册。LinearRegressionScratchadd_to_class

@d2l.add_to_class(LinearRegressionScratch) #@save
def forward(self, X):
  return torch.matmul(X, self.w) + self.b

@d2l.add_to_class(LinearRegressionScratch) #@save
def forward(self, X):
  return np.dot(X, self.w) + self.b

@d2l.add_to_class(LinearRegressionScratch) #@save
def forward(self, X):
  return jnp.matmul(X, self.w) + self.b

@d2l.add_to_class(LinearRegressionScratch) #@save
def forward(self, X):
  return tf.matmul(X, self.w) + self.b

3.4.2. 定义损失函数

由于更新我们的模型需要采用损失函数的梯度，因此我们应该首先定义损失函数。这里我们使用（3.1.5）中的平方损失函数。在实现中，我们需要将真实值转换y为预测值的形状 y_hat。以下方法返回的结果也将具有与y_hat. 我们还返回小批量中所有示例的平均损失值。

@d2l.add_to_class(LinearRegressionScratch) #@save
def loss(self, y_hat, y):
  l = (y_hat - y) ** 2 / 2
  return l.mean()

@d2l.add_to_class(LinearRegressionScratch) #@save
def loss(self, y_hat, y):
  l = (y_hat - y) ** 2 / 2
  return l.mean()

@d2l.add_to_class(LinearRegressionScratch) #@save
def loss(self, params, X, y, state):
  y_hat = state.apply_fn({'params': params}, *X) # X unpacked from a tuple
  l = (y_hat - y.reshape(y_hat.shape)) ** 2 / 2
  return l.mean()

@d2l.add_to_class(LinearRegressionScratch) #@save
def loss(self, y_hat, y):
  l = (y_hat - y) ** 2 / 2
  return tf.reduce_mean(l)

3.4.3. 定义优化算法

正如第 3.1 节中所讨论的，线性回归有一个封闭形式的解决方案。然而，我们这里的目标是说明如何训练更通用的神经网络，这需要我们教您如何使用小批量 SGD。因此，我们将借此机会介绍您的第一个 SGD 工作示例。在每一步，使用从我们的数据集中随机抽取的小批量，我们估计损失相对于参数的梯度。接下来，我们朝着可能减少损失的方向更新参数。

以下代码应用更新，给定一组参数，一个学习率lr。由于我们的损失是按小批量的平均值计算的，因此我们不需要根据批量大小调整学习率。在后面的章节中，我们将研究如何为分布式大规模学习中出现的非常大的小批量调整学习率。现在，我们可以忽略这种依赖性。

我们定义我们的SGD类，它是d2l.HyperParameters （在第 3.2.1 节中介绍的）的一个子类，以具有与内置 SGD 优化器类似的 API。我们更新方法中的参数step 。该zero_grad方法将所有梯度设置为 0，这必须在反向传播步骤之前运行。

class SGD(d2l.HyperParameters): #@save
  """Minibatch stochastic gradient descent."""
  def __init__(self, params, lr):
    self.save_hyperparameters()

  def step(self):
    for param in self.params:
      param -= self.lr * param.grad

  def zero_grad(self):
    for param in self.params:
      if param.grad is not None:
        param.grad.zero_()

We define our SGD class, a subclass of d2l.HyperParameters (introduced in Section 3.2.1), to have a similar API as the built-in SGD optimizer. We update the parameters in the step method. It accepts a batch_size argument that can be ignored.

class SGD(d2l.HyperParameters): #@save
  """Minibatch stochastic gradient descent."""
  def __init__(self, params, lr):
    self.save_hyperparameters()

  def step(self, _):
    for param in self.params:
      param -= self.lr * param.grad

class SGD(d2l.HyperParameters): #@save
  """Minibatch stochastic gradient descent."""
  # The key transformation of Optax is the GradientTransformation
  # defined by two methods, the init and the update.
  # The init initializes the state and the update transforms the gradients.
  # https://github.com/deepmind/optax/blob/master/optax/_src/transform.py
  def __init__(self, lr):
    self.save_hyperparameters()

  def init(self, params):
    # Delete unused params
    del params
    return optax.EmptyState

  def update(self, updates, state, params=None):
    del params
    # When state.apply_gradients method is called to update flax's
    # train_state object, it internally calls optax.apply_updates method
    # adding the params to the update equation defined below.
    updates = jax.tree_util.tree_map(lambda g: -self.lr * g, updates)
    return updates, state

  def __call__():
    return optax.GradientTransformation(self.init, self.update)

We define our SGD class, a subclass of d2l.HyperParameters (introduced in Section 3.2.1), to have a similar API as the built-in SGD optimizer. We update the parameters in the apply_gradients method. It accepts a list of parameter and gradient pairs.

class SGD(d2l.HyperParameters): #@save
  """Minibatch stochastic gradient descent."""
  def __init__(self, lr):
    self.save_hyperparameters()

  def apply_gradients(self, grads_and_vars):
    for grad, param in grads_and_vars:
      param.assign_sub(self.lr * grad)

接下来我们定义configure_optimizers方法，它返回类的一个实例SGD。

@d2l.add_to_class(LinearRegressionScratch) #@save
def configure_optimizers(self):
  return SGD([self.w, self.b], self.lr)

@d2l.add_to_class(LinearRegressionScratch) #@save
def configure_optimizers(self):
  return SGD([self.w, self.b], self.lr)

@d2l.add_to_class(LinearRegressionScratch) #@save
def configure_optimizers(self):
  return SGD(self.lr)

@d2l.add_to_class(LinearRegressionScratch) #@save
def configure_optimizers(self):
  return SGD(self.lr)

3.4.4. 训练

现在我们已经准备好所有的部分（参数、损失函数、模型和优化器），我们准备好实施主要的训练循环。理解这段代码至关重要，因为您将对本书涵盖的所有其他深度学习模型使用类似的训练循环。在每个epoch中，我们遍历整个训练数据集，通过每个示例一次（假设示例的数量可以被批量大小整除）。在每次迭代中，我们获取一小批训练示例，并通过模型的 training_step方法计算其损失。接下来，我们计算每个参数的梯度。最后，我们将调用优化算法来更新模型参数。总之，我们将执行以下循环：

初始化参数(w,b)

重复直到完成

计算梯度 g←∂(w,b)1|B|∑i∈Bl(x(i),y(i),w,b)

更新参数 (w,b)←(w,b)−ηg

回想一下，我们在3.3 节中生成的综合回归数据集 不提供验证数据集。然而，在大多数情况下，我们将使用验证数据集来衡量我们的模型质量。在这里，我们在每个时期通过一次验证数据加载器来衡量模型性能。按照我们的面向对象设计，prepare_batch和fit_epoch方法注册在d2l.Trainer类中（在 3.2.4 节中介绍）。

@d2l.add_to_class(d2l.Trainer) #@save
def prepare_batch(self, batch):
  return batch

@d2l.add_to_class(d2l.Trainer) #@save
def fit_epoch(self):
  self.model.train()
  for batch in self.train_dataloader:
    loss = self.model.training_step(self.prepare_batch(batch))
    self.optim.zero_grad()
    with torch.no_grad():
      loss.backward()
      if self.gradient_clip_val > 0: # To be discussed later
        self.clip_gradients(self.gradient_clip_val, self.model)
      self.optim.step()
    self.train_batch_idx += 1
  if self.val_dataloader is None:
    return
  self.model.eval()
  for batch in self.val_dataloader:
    with torch.no_grad():
      self.model.validation_step(self.prepare_batch(batch))
    self.val_batch_idx += 1

@d2l.add_to_class(d2l.Trainer) #@save
def prepare_batch(self, batch):
  return batch

@d2l.add_to_class(d2l.Trainer) #@save
def fit_epoch(self):
  for batch in self.train_dataloader:
    with autograd.record():
      loss = self.model.training_step(self.prepare_batch(batch))
    loss.backward()
    if self.gradient_clip_val > 0:
      self.clip_gradients(self.gradient_clip_val, self.model)
    self.optim.step(1)
    self.train_batch_idx += 1
  if self.val_dataloader is None:
    return
  for batch in self.val_dataloader:
    self.model.validation_step(self.prepare_batch(batch))
    self.val_batch_idx += 1

@d2l.add_to_class(d2l.Trainer) #@save
def prepare_batch(self, batch):
  return batch

@d2l.add_to_class(d2l.Trainer) #@save
def fit_epoch(self):
  self.model.training = True
  if self.state.batch_stats:
    # Mutable states will be used later (e.g., for batch norm)
    for batch in self.train_dataloader:
      (_, mutated_vars), grads = self.model.training_step(self.state.params,
                              self.prepare_batch(batch),
                              self.state)
      self.state = self.state.apply_gradients(grads=grads)
      # Can be ignored for models without Dropout Layers
      self.state = self.state.replace(
        dropout_rng=jax.random.split(self.state.dropout_rng)[0])
      self.state = self.state.replace(batch_stats=mutated_vars['batch_stats'])
      self.train_batch_idx += 1
  else:
    for batch in self.train_dataloader:
      _, grads = self.model.training_step(self.state.params,
                        self.prepare_batch(batch),
                        self.state)
      self.state = self.state.apply_gradients(grads=grads)
      # Can be ignored for models without Dropout Layers
      self.state = self.state.replace(
        dropout_rng=jax.random.split(self.state.dropout_rng)[0])
      self.train_batch_idx += 1

  if self.val_dataloader is None:
    return
  self.model.training = False
  for batch in self.val_dataloader:
    self.model.validation_step(self.state.params,
                  self.prepare_batch(batch),
                  self.state)
    self.val_batch_idx += 1

@d2l.add_to_class(d2l.Trainer) #@save
def prepare_batch(self, batch):
  return batch

@d2l.add_to_class(d2l.Trainer) #@save
def fit_epoch(self):
  self.model.training = True
  for batch in self.train_dataloader:
    with tf.GradientTape() as tape:
      loss = self.model.training_step(self.prepare_batch(batch))
    grads = tape.gradient(loss, self.model.trainable_variables)
    if self.gradient_clip_val > 0:
      grads = self.clip_gradients(self.gradient_clip_val, grads)
    self.optim.apply_gradients(zip(grads, self.model.trainable_variables))
    self.train_batch_idx += 1
  if self.val_dataloader is None:
    return
  self.model.training = False
  for batch in self.val_dataloader:
    self.model.validation_step(self.prepare_batch(batch))
    self.val_batch_idx += 1

我们几乎准备好训练模型，但首先我们需要一些数据来训练。这里我们使用SyntheticRegressionData类并传入一些基本参数。然后，我们用学习率训练我们的模型lr=0.03并设置max_epochs=3。请注意，一般来说，epoch 的数量和学习率都是超参数。一般来说，设置超参数很棘手，我们通常希望使用 3 路分割，一组用于训练，第二组用于超参数选择，第三组保留用于最终评估。我们暂时省略这些细节，但稍后会对其进行修改。

model = LinearRegressionScratch(2, lr=0.03)
data = d2l.SyntheticRegressionData(w=torch.tensor([2, -3.4]), b=4.2)
trainer = d2l.Trainer(max_epochs=3)
trainer.fit(model, data)

model = LinearRegressionScratch(2, lr=0.03)
data = d2l.SyntheticRegressionData(w=np.array([2, -3.4]), b=4.2)
trainer = d2l.Trainer(max_epochs=3)
trainer.fit(model, data)

model = LinearRegressionScratch(2, lr=0.03)
data = d2l.SyntheticRegressionData(w=jnp.array([2, -3.4]), b=4.2)
trainer = d2l.Trainer(max_epochs=3)
trainer.fit(model, data)

model = LinearRegressionScratch(2, lr=0.03)
data = d2l.SyntheticRegressionData(w=tf.constant([2, -3.4]), b=4.2)
trainer = d2l.Trainer(max_epochs=3)
trainer.fit(model, data)

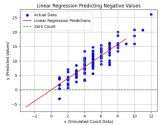
因为我们自己合成了数据集，所以我们确切地知道真正的参数是什么。因此，我们可以通过将真实参数与我们通过训练循环学到的参数进行比较来评估我们在训练中的成功。事实上，他们彼此非常接近。

print(f'error in estimating w: {data.w - model.w.reshape(data.w.shape)}')
print(f'error in estimating b: {data.b - model.b}')

error in estimating w: tensor([ 0.1006, -0.1535], grad_fn=)
error in estimating b: tensor([0.2132], grad_fn=)

print(f'error in estimating w: {data.w - model.w.reshape(data.w.shape)}')
print(f'error in estimating b: {data.b - model.b}')

error in estimating w: [ 0.10755348 -0.13104177]
error in estimating b: [0.18908024]

params = trainer.state.params
print(f"error in estimating w: {data.w - params['w'].reshape(data.w.shape)}")
print(f"error in estimating b: {data.b - params['b']}")

error in estimating w: [ 0.06764424 -0.183249 ]
error in estimating b: [0.23523378]

print(f'error in estimating w: {data.w - tf.reshape(model.w, data.w.shape)}')
print(f'error in estimating b: {data.b - model.b}')

error in estimating w: [ 0.08918679 -0.11773038]
error in estimating b: [0.211231]

我们不应该把准确恢复地面实况参数的能力视为理所当然。一般来说，对于深度模型，参数的唯一解是不存在的，即使对于线性模型，只有当没有特征与其他特征线性相关时，才有可能准确地恢复参数。然而，在机器学习中，我们通常不太关心恢复真正的底层参数，而更关心导致高度准确预测的参数 ( Vapnik, 1992 )。幸运的是，即使在困难的优化问题上，随机梯度下降通常也能找到非常好的解决方案，部分原因在于，对于深度网络，存在许多导致高精度预测的参数配置。

3.4.5. 概括

在本节中，我们通过实施功能齐全的神经网络模型和训练循环，朝着设计深度学习系统迈出了重要一步。在这个过程中，我们构建了数据加载器、模型、损失函数、优化程序以及可视化和监控工具。为此，我们编写了一个 Python 对象，其中包含用于训练模型的所有相关组件。虽然这还不是专业级的实现，但它具有完美的功能，并且像这样的代码已经可以帮助您快速解决小问题。在接下来的部分中，我们将看到如何更简洁 （避免样板代码）和更高效（充分利用我们的 GPU）。

3.4.6. 练习

如果我们将权重初始化为零会发生什么。该算法仍然有效吗？如果我们用方差初始化参数会怎样1,000而不是0.01？

假设您是Georg Simon Ohm，正在尝试建立一个与电压和电流相关的电阻器模型。您可以使用自动微分来学习模型的参数吗？

你能用普朗克定律通过光谱能量密度来确定物体的温度吗？作为参考，光谱密度B从黑体发出的辐射是 B(λ,T)=2hc2λ5⋅(exp⁡hcλkT−1)−1. 这里λ是波长，T是温度， c是光速，h是普朗克量子，并且 k是玻尔兹曼常数。您测量不同波长的能量λ现在您需要使谱密度曲线符合普朗克定律。

如果你想计算损失的二阶导数，你可能会遇到什么问题？你会如何修复它们？

为什么函数reshape中需要方法loss？

尝试使用不同的学习率来找出损失函数值下降的速度。你能通过增加训练的次数来减少错误吗？

如果样本数不能除以批量大小，那么在data_iter一个纪元结束时会发生什么？

尝试实现不同的损失函数，例如绝对值损失。(y_hat - d2l.reshape(y, y_hat.shape)).abs().sum()

检查常规数据会发生什么。

如果您主动扰乱某些条目，请检查行为是否存在差异y， 例如 y5=10,000.

你能想出一个便宜的解决方案来结合平方损失和绝对值损失的最佳方面吗？提示：如何避免非常大的梯度值？

为什么我们需要重新洗牌数据集？你能设计一个恶意数据集否则会破坏优化算法的情况吗？