在使用反向传播(Elman,1990)训练第一个 Elman 式 RNN 后不久,学习长期依赖性(由于梯度消失和爆炸)的问题变得突出,Bengio 和 Hochreiter 讨论了这个问题 (Bengio等人, 1994 年,Hochreiter等人,2001 年). Hochreiter 早在他 1991 年的硕士论文中就阐明了这个问题,尽管结果并不广为人知,因为论文是用德语写的。虽然梯度裁剪有助于梯度爆炸,但处理消失的梯度似乎需要更精细的解决方案。Hochreiter 和 Schmidhuber ( 1997 )提出的长短期记忆 (LSTM) 模型是解决梯度消失问题的第一个也是最成功的技术之一。LSTM 类似于标准的递归神经网络,但这里每个普通的递归节点都被一个记忆单元取代。每个存储单元包含一个内部状态,即具有固定权重 1 的自连接循环边的节点,确保梯度可以跨越多个时间步而不会消失或爆炸。
“长短期记忆”一词来自以下直觉。简单的递归神经网络具有权重形式的长期记忆。权重在训练过程中缓慢变化,对数据的一般知识进行编码。它们还具有短暂激活形式的短期记忆,从每个节点传递到连续的节点。LSTM 模型通过记忆单元引入了一种中间类型的存储。存储单元是一个复合单元,由具有特定连接模式的较简单节点构成,并包含新的乘法节点。
import torch from torch import nn from d2l import torch as d2l
from mxnet import np, npx from mxnet.gluon import rnn from d2l import mxnet as d2l npx.set_np()
import jax from flax import linen as nn from jax import numpy as jnp from d2l import jax as d2l
import tensorflow as tf from d2l import tensorflow as d2l
10.1.1。门控存储单元
每个存储单元都配备了一个内部状态和多个乘法门,用于确定 (i) 给定的输入是否应该影响内部状态(输入门),(ii) 内部状态是否应该被刷新到0(遗忘门),以及 (iii) 应该允许给定神经元的内部状态影响细胞的输出(输出门)。
10.1.1.1。门控隐藏状态
普通 RNN 和 LSTM 之间的主要区别在于后者支持隐藏状态的门控。这意味着我们有专门的机制来确定何时应该更新隐藏状态以及何时应该重置它。这些机制是学习的,它们解决了上面列出的问题。例如,如果第一个标记非常重要,我们将学习在第一次观察后不更新隐藏状态。同样,我们将学会跳过不相关的临时观察。最后,我们将学习在需要时重置潜在状态。我们将在下面详细讨论。
10.1.1.2。输入门、遗忘门和输出门
进入 LSTM 门的数据是当前时间步的输入和前一时间步的隐藏状态,如图 10.1.1所示。三个具有 sigmoid 激活函数的全连接层计算输入门、遗忘门和输出门的值。作为 sigmoid 激活的结果,三个门的所有值都在范围内(0,1). 此外,我们需要一个 输入节点,通常使用tanh激活函数计算。直观上,输入门决定了输入节点的多少值应该添加到当前存储单元的内部状态。遗忘 门决定是保留内存的当前值还是刷新内存。而输出门决定了记忆单元是否应该影响当前时间步的输出。
图 10.1.1计算 LSTM 模型中的输入门、遗忘门和输出门。
在数学上,假设有h隐藏单元,批量大小为n,输入的数量是d. 因此,输入是Xt∈Rn×d上一个时间步的隐藏状态是 Ht−1∈Rn×h. 相应地,时间步长的门t定义如下:输入门是It∈Rn×h, 遗忘门是 Ft∈Rn×h,输出门是 Ot∈Rn×h. 它们的计算方式如下:
(10.1.1)It=σ(XtWxi+Ht−1Whi+bi),Ft=σ(XtWxf+Ht−1Whf+bf),Ot=σ(XtWxo+Ht−1Who+bo),
在哪里 Wxi,Wxf,Wxo∈Rd×h 和 Whi,Whf,Who∈Rh×h 是权重参数和 bi,bf,bo∈R1×h 是偏置参数。请注意,广播(请参阅 第 2.1.4 节)是在求和期间触发的。我们使用 sigmoid 函数(如第 5.1 节中介绍的)将输入值映射到区间(0,1).
10.1.1.3。输入节点
接下来我们设计存储单元。由于我们还没有具体说明各个门的作用,所以先介绍一下输入节点 C~t∈Rn×h. 它的计算类似于上述三个门的计算,但使用tanh取值范围为(−1,1)作为激活函数。这导致以下时间步等式t:
(10.1.2)C~t=tanh(XtWxc+Ht−1Whc+bc),
在哪里Wxc∈Rd×h和 Whc∈Rh×h是权重参数和bc∈R1×h是偏置参数。
输入节点的快速图示如图 10.1.2所示 。
图 10.1.2计算 LSTM 模型中的输入节点。
10.1.1.4。存储单元内部状态
在 LSTM 中,输入门It管理我们通过以下方式考虑新数据的程度C~t和遗忘门Ft解决旧单元格内部状态的多少Ct−1∈Rn×h我们保留。使用 Hadamard(按元素)乘积运算符⊙我们得出以下更新方程:
(10.1.3)Ct=Ft⊙Ct−1+It⊙C~t.
如果遗忘门始终为 1,输入门始终为 0,则存储单元内部状态Ct−1将永远保持不变,不变地传递到每个后续时间步。然而,输入门和遗忘门使模型能够灵活地学习何时保持此值不变以及何时扰动它以响应后续输入。在实践中,这种设计缓解了梯度消失问题,导致模型更容易训练,尤其是在面对序列长度较长的数据集时。
这样我们就得到了图 10.1.3中的流程图。
图 10.1.3计算 LSTM 模型中的存储单元内部状态。
10.1.1.5。隐藏状态
最后,我们需要定义如何计算记忆单元的输出,即隐藏状态Ht∈Rn×h,正如其他层所见。这就是输出门发挥作用的地方。在 LSTM 中,我们首先应用tanh到存储单元内部状态,然后应用另一个逐点乘法,这次是输出门。这确保了值Ht总是在区间(−1,1):
(10.1.4)Ht=Ot⊙tanh(Ct).
每当输出门接近 1 时,我们允许记忆单元内部状态不受抑制地影响后续层,而对于接近 0 的输出门值,我们防止当前记忆在当前时间步影响网络的其他层。请注意,一个记忆单元可以在不影响网络其余部分的情况下跨越多个时间步长积累信息(只要输出门的值接近于 0),然后一旦输出门突然在后续时间步长影响网络从接近 0 的值翻转到接近 1 的值。
图 10.1.4有数据流的图形说明。
图 10.1.4计算 LSTM 模型中的隐藏状态。
10.1.2。从零开始实施
现在让我们从头开始实现 LSTM。与9.5 节的实验一样 ,我们首先加载时间机器数据集。
10.1.2.1。初始化模型参数
接下来,我们需要定义和初始化模型参数。如前所述,超参数num_hiddens决定了隐藏单元的数量。我们按照标准偏差为 0.01 的高斯分布初始化权重,并将偏差设置为 0。
class LSTMScratch(d2l.Module):
def __init__(self, num_inputs, num_hiddens, sigma=0.01):
super().__init__()
self.save_hyperparameters()
init_weight = lambda *shape: nn.Parameter(torch.randn(*shape) * sigma)
triple = lambda: (init_weight(num_inputs, num_hiddens),
init_weight(num_hiddens, num_hiddens),
nn.Parameter(torch.zeros(num_hiddens)))
self.W_xi, self.W_hi, self.b_i = triple() # Input gate
self.W_xf, self.W_hf, self.b_f = triple() # Forget gate
self.W_xo, self.W_ho, self.b_o = triple() # Output gate
self.W_xc, self.W_hc, self.b_c = triple() # Input node
实际模型的定义如上所述,由三个门和一个输入节点组成。请注意,只有隐藏状态会传递到输出层。
@d2l.add_to_class(LSTMScratch) def forward(self, inputs, H_C=None): if H_C is None: # Initial state with shape: (batch_size, num_hiddens) H = torch.zeros((inputs.shape[1], self.num_hiddens), device=inputs.device) C = torch.zeros((inputs.shape[1], self.num_hiddens), device=inputs.device) else: H, C = H_C outputs = [] for X in inputs: I = torch.sigmoid(torch.matmul(X, self.W_xi) + torch.matmul(H, self.W_hi) + self.b_i) F = torch.sigmoid(torch.matmul(X, self.W_xf) + torch.matmul(H, self.W_hf) + self.b_f) O = torch.sigmoid(torch.matmul(X, self.W_xo) + torch.matmul(H, self.W_ho) + self.b_o) C_tilde = torch.tanh(torch.matmul(X, self.W_xc) + torch.matmul(H, self.W_hc) + self.b_c) C = F * C + I * C_tilde H = O * torch.tanh(C) outputs.append(H) return outputs, (H, C)
class LSTMScratch(d2l.Module):
def __init__(self, num_inputs, num_hiddens, sigma=0.01):
super().__init__()
self.save_hyperparameters()
init_weight = lambda *shape: np.random.randn(*shape) * sigma
triple = lambda: (init_weight(num_inputs, num_hiddens),
init_weight(num_hiddens, num_hiddens),
np.zeros(num_hiddens))
self.W_xi, self.W_hi, self.b_i = triple() # Input gate
self.W_xf, self.W_hf, self.b_f = triple() # Forget gate
self.W_xo, self.W_ho, self.b_o = triple() # Output gate
self.W_xc, self.W_hc, self.b_c = triple() # Input node
The actual model is defined as described above, consisting of three gates and an input node. Note that only the hidden state is passed to the output layer.
@d2l.add_to_class(LSTMScratch)
def forward(self, inputs, H_C=None):
if H_C is None:
# Initial state with shape: (batch_size, num_hiddens)
H = np.zeros((inputs.shape[1], self.num_hiddens),
ctx=inputs.ctx)
C = np.zeros((inputs.shape[1], self.num_hiddens),
ctx=inputs.ctx)
else:
H, C = H_C
outputs = []
for X in inputs:
I = npx.sigmoid(np.dot(X, self.W_xi) +
np.dot(H, self.W_hi) + self.b_i)
F = npx.sigmoid(np.dot(X, self.W_xf) +
np.dot(H, self.W_hf) + self.b_f)
O = npx.sigmoid(np.dot(X, self.W_xo) +
np.dot(H, self.W_ho) + self.b_o)
C_tilde = np.tanh(np.dot(X, self.W_xc) +
np.dot(H, self.W_hc) + self.b_c)
C = F * C + I * C_tilde
H = O * np.tanh(C)
outputs.append(H)
return outputs, (H, C)
class LSTMScratch(d2l.Module):
num_inputs: int
num_hiddens: int
sigma: float = 0.01
def setup(self):
init_weight = lambda name, shape: self.param(name,
nn.initializers.normal(self.sigma),
shape)
triple = lambda name : (
init_weight(f'W_x{name}', (self.num_inputs, self.num_hiddens)),
init_weight(f'W_h{name}', (self.num_hiddens, self.num_hiddens)),
self.param(f'b_{name}', nn.initializers.zeros, (self.num_hiddens)))
self.W_xi, self.W_hi, self.b_i = triple('i') # Input gate
self.W_xf, self.W_hf, self.b_f = triple('f') # Forget gate
self.W_xo, self.W_ho, self.b_o = triple('o') # Output gate
self.W_xc, self.W_hc, self.b_c = triple('c') # Input node
The actual model is defined as described above, consisting of three gates and an input node. Note that only the hidden state is passed to the output layer. A long for-loop in the forward method will result in an extremely long JIT compilation time for the first run. As a solution to this, instead of using a for-loop to update the state with every time step, JAX has jax.lax.scan utility transformation to achieve the same behavior. It takes in an initial state called carry and an inputs array which is scanned on its leading axis. The scan transformation ultimately returns the final state and the stacked outputs as expected.
@d2l.add_to_class(LSTMScratch)
def forward(self, inputs, H_C=None):
# Use lax.scan primitive instead of looping over the
# inputs, since scan saves time in jit compilation.
def scan_fn(carry, X):
H, C = carry
I = jax.nn.sigmoid(jnp.matmul(X, self.W_xi) + (
jnp.matmul(H, self.W_hi)) + self.b_i)
F = jax.nn.sigmoid(jnp.matmul(X, self.W_xf) +
jnp.matmul(H, self.W_hf) + self.b_f)
O = jax.nn.sigmoid(jnp.matmul(X, self.W_xo) +
jnp.matmul(H, self.W_ho) + self.b_o)
C_tilde = jnp.tanh(jnp.matmul(X, self.W_xc) +
jnp.matmul(H, self.W_hc) + self.b_c)
C = F * C + I * C_tilde
H = O * jnp.tanh(C)
return (H, C), H # return carry, y
if H_C is None:
batch_size = inputs.shape[1]
carry = jnp.zeros((batch_size, self.num_hiddens)),
jnp.zeros((batch_size, self.num_hiddens))
else:
carry = H_C
# scan takes the scan_fn, initial carry state, xs with leading axis to be scanned
carry, outputs = jax.lax.scan(scan_fn, carry, inputs)
return outputs, carry
class LSTMScratch(d2l.Module):
def __init__(self, num_inputs, num_hiddens, sigma=0.01):
super().__init__()
self.save_hyperparameters()
init_weight = lambda *shape: tf.Variable(tf.random.normal(shape) * sigma)
triple = lambda: (init_weight(num_inputs, num_hiddens),
init_weight(num_hiddens, num_hiddens),
tf.Variable(tf.zeros(num_hiddens)))
self.W_xi, self.W_hi, self.b_i = triple() # Input gate
self.W_xf, self.W_hf, self.b_f = triple() # Forget gate
self.W_xo, self.W_ho, self.b_o = triple() # Output gate
self.W_xc, self.W_hc, self.b_c = triple() # Input node
The actual model is defined as described above, consisting of three gates and an input node. Note that only the hidden state is passed to the output layer.
@d2l.add_to_class(LSTMScratch)
def forward(self, inputs, H_C=None):
if H_C is None:
# Initial state with shape: (batch_size, num_hiddens)
H = tf.zeros((inputs.shape[1], self.num_hiddens))
C = tf.zeros((inputs.shape[1], self.num_hiddens))
else:
H, C = H_C
outputs = []
for X in inputs:
I = tf.sigmoid(tf.matmul(X, self.W_xi) +
tf.matmul(H, self.W_hi) + self.b_i)
F = tf.sigmoid(tf.matmul(X, self.W_xf) +
tf.matmul(H, self.W_hf) + self.b_f)
O = tf.sigmoid(tf.matmul(X, self.W_xo) +
tf.matmul(H, self.W_ho) + self.b_o)
C_tilde = tf.tanh(tf.matmul(X, self.W_xc) +
tf.matmul(H, self.W_hc) + self.b_c)
C = F * C + I * C_tilde
H = O * tf.tanh(C)
outputs.append(H)
return outputs, (H, C)
10.1.2.2。训练和预测
让我们通过实例化第 9.5 节RNNLMScratch中介绍的类来训练 LSTM 模型。
data = d2l.TimeMachine(batch_size=1024, num_steps=32) lstm = LSTMScratch(num_inputs=len(data.vocab), num_hiddens=32) model = d2l.RNNLMScratch(lstm, vocab_size=len(data.vocab), lr=4) trainer = d2l.Trainer(max_epochs=50, gradient_clip_val=1, num_gpus=1) trainer.fit(model, data)
data = d2l.TimeMachine(batch_size=1024, num_steps=32) lstm = LSTMScratch(num_inputs=len(data.vocab), num_hiddens=32) model = d2l.RNNLMScratch(lstm, vocab_size=len(data.vocab), lr=4) trainer = d2l.Trainer(max_epochs=50, gradient_clip_val=1, num_gpus=1) trainer.fit(model, data)
data = d2l.TimeMachine(batch_size=1024, num_steps=32) lstm = LSTMScratch(num_inputs=len(data.vocab), num_hiddens=32) model = d2l.RNNLMScratch(lstm, vocab_size=len(data.vocab), lr=4) trainer = d2l.Trainer(max_epochs=50, gradient_clip_val=1, num_gpus=1) trainer.fit(model, data)
data = d2l.TimeMachine(batch_size=1024, num_steps=32) with d2l.try_gpu(): lstm = LSTMScratch(num_inputs=len(data.vocab), num_hiddens=32) model = d2l.RNNLMScratch(lstm, vocab_size=len(data.vocab), lr=4) trainer = d2l.Trainer(max_epochs=50, gradient_clip_val=1) trainer.fit(model, data)
10.1.3。简洁的实现
使用高级 API,我们可以直接实例化 LSTM 模型。这封装了我们在上面明确说明的所有配置细节。该代码明显更快,因为它使用编译运算符而不是 Python 来处理我们之前阐明的许多细节。
class LSTM(d2l.RNN):
def __init__(self, num_inputs, num_hiddens):
d2l.Module.__init__(self)
self.save_hyperparameters()
self.rnn = nn.LSTM(num_inputs, num_hiddens)
def forward(self, inputs, H_C=None):
return self.rnn(inputs, H_C)
lstm = LSTM(num_inputs=len(data.vocab), num_hiddens=32)
model = d2l.RNNLM(lstm, vocab_size=len(data.vocab), lr=4)
trainer.fit(model, data)
model.predict('it has', 20, data.vocab, d2l.try_gpu())
'it has the the the the the'
class LSTM(d2l.RNN):
def __init__(self, num_hiddens):
d2l.Module.__init__(self)
self.save_hyperparameters()
self.rnn = rnn.LSTM(num_hiddens)
def forward(self, inputs, H_C=None):
if H_C is None: H_C = self.rnn.begin_state(
inputs.shape[1], ctx=inputs.ctx)
return self.rnn(inputs, H_C)
lstm = LSTM(num_hiddens=32)
model = d2l.RNNLM(lstm, vocab_size=len(data.vocab), lr=4)
trainer.fit(model, data)
model.predict('it has', 20, data.vocab, d2l.try_gpu())
'it has and the time travel'
class LSTM(d2l.RNN):
num_hiddens: int
@nn.compact
def __call__(self, inputs, H_C=None, training=False):
if H_C is None:
batch_size = inputs.shape[1]
H_C = nn.OptimizedLSTMCell.initialize_carry(jax.random.PRNGKey(0),
(batch_size,),
self.num_hiddens)
LSTM = nn.scan(nn.OptimizedLSTMCell, variable_broadcast="params",
in_axes=0, out_axes=0, split_rngs={"params": False})
H_C, outputs = LSTM()(H_C, inputs)
return outputs, H_C
lstm = LSTM(num_hiddens=32)
model = d2l.RNNLM(lstm, vocab_size=len(data.vocab), lr=4)
trainer.fit(model, data)
model.predict('it has', 20, data.vocab, trainer.state.params)
'it has it it it it it it i'
class LSTM(d2l.RNN):
def __init__(self, num_hiddens):
d2l.Module.__init__(self)
self.save_hyperparameters()
self.rnn = tf.keras.layers.LSTM(
num_hiddens, return_sequences=True,
return_state=True, time_major=True)
def forward(self, inputs, H_C=None):
outputs, *H_C = self.rnn(inputs, H_C)
return outputs, H_C
lstm = LSTM(num_hiddens=32)
with d2l.try_gpu():
model = d2l.RNNLM(lstm, vocab_size=len(data.vocab), lr=4)
trainer.fit(model, data)
model.predict('it has', 20, data.vocab)
'it has the the the the the'
LSTM 是具有非平凡状态控制的原型潜变量自回归模型。多年来已经提出了许多其变体,例如,多层、残差连接、不同类型的正则化。然而,由于序列的长程依赖性,训练 LSTM 和其他序列模型(例如 GRU)的成本非常高。稍后我们会遇到在某些情况下可以使用的替代模型,例如 Transformers。
10.1.4。概括
虽然 LSTM 于 1997 年发布,但随着 2000 年代中期在预测竞赛中的一些胜利,它们变得更加突出,并从 2011 年成为序列学习的主要模型,直到最近随着 Transformer 模型的兴起,从 2017 年开始。甚至变形金刚他们的一些关键想法归功于 LSTM 引入的架构设计创新。LSTM 具有三种类型的门:输入门、遗忘门和控制信息流的输出门。LSTM 的隐藏层输出包括隐藏状态和记忆单元内部状态。只有隐藏状态被传递到输出层,而记忆单元内部状态完全是内部的。LSTM 可以缓解梯度消失和爆炸。
10.1.5。练习
调整超参数并分析它们对运行时间、困惑度和输出序列的影响。
您需要如何更改模型以生成正确的单词而不是字符序列?
比较给定隐藏维度的 GRU、LSTM 和常规 RNN 的计算成本。特别注意训练和推理成本。
由于候选记忆单元确保取值范围介于−1和1通过使用tanh功能,为什么隐藏状态需要使用tanh函数再次确保输出值范围介于−1和 1?
为时间序列预测而不是字符序列预测实施 LSTM 模型。
-
rnn
+关注
关注
0文章
89浏览量
6891 -
pytorch
+关注
关注
2文章
808浏览量
13229
发布评论请先 登录
相关推荐
基于长短期记忆模型的多维主题模型
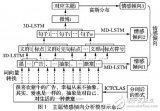
如何使用树结构长短期记忆神经网络进行金融时间序列预测
循环神经网络(RNN)和(LSTM)初学者指南
一种具有强记忆力的 E3D-LSTM网络,强化了LSTM的长时记忆能力

长短时记忆网络(LSTM)介绍
长短时记忆网络(LSTM)

基于预训练模型和长短期记忆网络的深度学习模型
基于长短期记忆网络的长距离股票趋势预测





 PyTorch教程-10.1. 长短期记忆 (LSTM)
PyTorch教程-10.1. 长短期记忆 (LSTM)











评论