PyTorch教程-11.6. 自注意力和位置编码

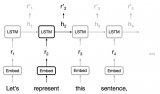
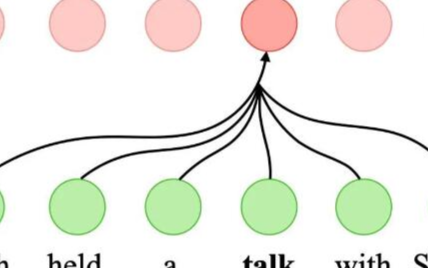
在深度学习中，我们经常使用 CNN 或 RNN 对序列进行编码。现在考虑到注意力机制，想象一下将一系列标记输入注意力机制，这样在每个步骤中，每个标记都有自己的查询、键和值。在这里，当在下一层计算令牌表示的值时，令牌可以（通过其查询向量）参与每个其他令牌（基于它们的键向量进行匹配）。使用完整的查询键兼容性分数集，我们可以通过在其他标记上构建适当的加权和来为每个标记计算表示。因为每个标记都关注另一个标记（不同于解码器步骤关注编码器步骤的情况），这种架构通常被描述为自注意力模型 （Lin等。, 2017 年， Vaswani等人。, 2017 )，以及其他地方描述的内部注意力模型 ( Cheng et al. , 2016 , Parikh et al. , 2016 , Paulus et al. , 2017 )。在本节中，我们将讨论使用自注意力的序列编码，包括使用序列顺序的附加信息。

import math
import torch
from torch import nn
from d2l import torch as d2l

import math
from mxnet import autograd, np, npx
from mxnet.gluon import nn
from d2l import mxnet as d2l

npx.set_np()

import jax
from flax import linen as nn
from jax import numpy as jnp
from d2l import jax as d2l

No GPU/TPU found, falling back to CPU. (Set TF_CPP_MIN_LOG_LEVEL=0 and rerun for more info.)

import numpy as np
import tensorflow as tf
from d2l import tensorflow as d2l

11.6.1。自注意力

给定一系列输入标记 x1,…,xn任何地方 xi∈Rd(1≤i≤n), 它的self-attention输出一个相同长度的序列 y1,…,yn， 在哪里

(11.6.1)yi=f(xi,(x1,x1),…,(xn,xn))∈Rd

根据 (11.1.1)中attention pooling的定义。使用多头注意力，以下代码片段计算具有形状（批量大小、时间步数或标记中的序列长度， d). 输出张量具有相同的形状。

num_hiddens, num_heads = 100, 5
attention = d2l.MultiHeadAttention(num_hiddens, num_heads, 0.5)
batch_size, num_queries, valid_lens = 2, 4, torch.tensor([3, 2])
X = torch.ones((batch_size, num_queries, num_hiddens))
d2l.check_shape(attention(X, X, X, valid_lens),
        (batch_size, num_queries, num_hiddens))

num_hiddens, num_heads = 100, 5
attention = d2l.MultiHeadAttention(num_hiddens, num_heads, 0.5)
attention.initialize()

batch_size, num_queries, valid_lens = 2, 4, np.array([3, 2])
X = np.ones((batch_size, num_queries, num_hiddens))
d2l.check_shape(attention(X, X, X, valid_lens),
        (batch_size, num_queries, num_hiddens))

num_hiddens, num_heads = 100, 5
attention = d2l.MultiHeadAttention(num_hiddens, num_heads, 0.5)

batch_size, num_queries, valid_lens = 2, 4, jnp.array([3, 2])
X = jnp.ones((batch_size, num_queries, num_hiddens))
d2l.check_shape(attention.init_with_output(d2l.get_key(), X, X, X, valid_lens,
                      training=False)[0][0],
        (batch_size, num_queries, num_hiddens))

num_hiddens, num_heads = 100, 5
attention = d2l.MultiHeadAttention(num_hiddens, num_hiddens, num_hiddens,
                  num_hiddens, num_heads, 0.5)

batch_size, num_queries, valid_lens = 2, 4, tf.constant([3, 2])
X = tf.ones((batch_size, num_queries, num_hiddens))
d2l.check_shape(attention(X, X, X, valid_lens, training=False),
        (batch_size, num_queries, num_hiddens))

11.6.2。比较 CNN、RNN 和自注意力

让我们比较一下映射一系列的架构n标记到另一个等长序列，其中每个输入或输出标记由一个d维向量。具体来说，我们将考虑 CNN、RNN 和自注意力。我们将比较它们的计算复杂度、顺序操作和最大路径长度。请注意，顺序操作会阻止并行计算，而序列位置的任意组合之间的较短路径可以更容易地学习序列内的远程依赖关系 （Hochreiter等人，2001 年）。

图 11.6.1比较 CNN（省略填充标记）、RNN 和自注意力架构。

考虑一个卷积层，其内核大小为k. 我们将在后面的章节中提供有关使用 CNN 进行序列处理的更多详细信息。现在，我们只需要知道，因为序列长度是n，输入和输出通道的数量都是 d, 卷积层的计算复杂度为 O(knd2). 如图11.6.1 所示，CNN 是分层的，因此有O(1) 顺序操作和最大路径长度是 O(n/k). 例如，x1和 x5位于图 11.6.1中内核大小为 3 的双层 CNN 的接受域内。

在更新 RNN 的隐藏状态时，乘以 d×d权重矩阵和d维隐藏状态的计算复杂度为O(d2). 由于序列长度为n，循环层的计算复杂度为O(nd2). 根据 图 11.6.1，有O(n) 不能并行化的顺序操作，最大路径长度也是O(n).

在自注意力中，查询、键和值都是 n×d矩阵。考虑(11.3.6)中的缩放点积注意力，其中n×d矩阵乘以d×n矩阵，然后是输出 n×n矩阵乘以n×d矩阵。因此，self-attention 有一个O(n2d) 计算复杂度。正如我们在图 11.6.1中看到的 ，每个标记都通过自注意力直接连接到任何其他标记。因此，计算可以与O(1)顺序操作和最大路径长度也是O(1).

总而言之，CNN 和 self-attention 都享有并行计算，并且 self-attention 具有最短的最大路径长度。然而，关于序列长度的二次计算复杂度使得自注意力对于非常长的序列来说非常慢。

11.6.3。位置编码

与循环一个接一个地处理序列标记的 RNN 不同，self-attention 摒弃顺序操作以支持并行计算。但是请注意，self-attention 本身并不能保持序列的顺序。如果模型知道输入序列到达的顺序真的很重要，我们该怎么办？

保留有关标记顺序的信息的主要方法是将其表示为与每个标记相关联的附加输入的模型。这些输入称为位置编码。它们可以被学习或先验固定。我们现在描述一种基于正弦和余弦函数的固定位置编码的简单方案（Vaswani等人，2017 年）。

假设输入表示 X∈Rn×d包含 d-维度嵌入n序列的标记。位置编码输出X+P使用位置嵌入矩阵 P∈Rn×d形状相同，其元素在ith行和 (2j)th或者(2j+1)th专栏是

(11.6.2)pi,2j=sin⁡(i100002j/d),pi,2j+1=cos⁡(i100002j/d).

乍一看，这种三角函数设计看起来很奇怪。在解释这个设计之前，让我们先在下面的 PositionalEncoding类中实现它。

class PositionalEncoding(nn.Module): #@save
  """Positional encoding."""
  def __init__(self, num_hiddens, dropout, max_len=1000):
    super().__init__()
    self.dropout = nn.Dropout(dropout)
    # Create a long enough P
    self.P = torch.zeros((1, max_len, num_hiddens))
    X = torch.arange(max_len, dtype=torch.float32).reshape(
      -1, 1) / torch.pow(10000, torch.arange(
      0, num_hiddens, 2, dtype=torch.float32) / num_hiddens)
    self.P[:, :, 0::2] = torch.sin(X)
    self.P[:, :, 1::2] = torch.cos(X)

  def forward(self, X):
    X = X + self.P[:, :X.shape[1], :].to(X.device)
    return self.dropout(X)

class PositionalEncoding(nn.Block): #@save
  """Positional encoding."""
  def __init__(self, num_hiddens, dropout, max_len=1000):
    super().__init__()
    self.dropout = nn.Dropout(dropout)
    # Create a long enough P
    self.P = np.zeros((1, max_len, num_hiddens))
    X = np.arange(max_len).reshape(-1, 1) / np.power(
      10000, np.arange(0, num_hiddens, 2) / num_hiddens)
    self.P[:, :, 0::2] = np.sin(X)
    self.P[:, :, 1::2] = np.cos(X)

  def forward(self, X):
    X = X + self.P[:, :X.shape[1], :].as_in_ctx(X.ctx)
    return self.dropout(X)

class PositionalEncoding(nn.Module): #@save
  """Positional encoding."""
  num_hiddens: int
  dropout: float
  max_len: int = 1000

  def setup(self):
    # Create a long enough P
    self.P = jnp.zeros((1, self.max_len, self.num_hiddens))
    X = jnp.arange(self.max_len, dtype=jnp.float32).reshape(
      -1, 1) / jnp.power(10000, jnp.arange(
      0, self.num_hiddens, 2, dtype=jnp.float32) / self.num_hiddens)
    self.P = self.P.at[:, :, 0::2].set(jnp.sin(X))
    self.P = self.P.at[:, :, 1::2].set(jnp.cos(X))

  @nn.compact
  def __call__(self, X, training=False):
    # Flax sow API is used to capture intermediate variables
    self.sow('intermediates', 'P', self.P)
    X = X + self.P[:, :X.shape[1], :]
    return nn.Dropout(self.dropout)(X, deterministic=not training)

class PositionalEncoding(tf.keras.layers.Layer): #@save
  """Positional encoding."""
  def __init__(self, num_hiddens, dropout, max_len=1000):
    super().__init__()
    self.dropout = tf.keras.layers.Dropout(dropout)
    # Create a long enough P
    self.P = np.zeros((1, max_len, num_hiddens))
    X = np.arange(max_len, dtype=np.float32).reshape(
      -1,1)/np.power(10000, np.arange(
      0, num_hiddens, 2, dtype=np.float32) / num_hiddens)
    self.P[:, :, 0::2] = np.sin(X)
    self.P[:, :, 1::2] = np.cos(X)

  def call(self, X, **kwargs):
    X = X + self.P[:, :X.shape[1], :]
    return self.dropout(X, **kwargs)

在位置嵌入矩阵中P，行对应于序列中的位置，列代表不同的位置编码维度。在下面的示例中，我们可以看到6th和7th位置嵌入矩阵的列具有比 8th和9th列。之间的偏移量6th和 7th（同样的8th和 9th) 列是由于正弦和余弦函数的交替。

encoding_dim, num_steps = 32, 60
pos_encoding = PositionalEncoding(encoding_dim, 0)
X = pos_encoding(torch.zeros((1, num_steps, encoding_dim)))
P = pos_encoding.P[:, :X.shape[1], :]
d2l.plot(torch.arange(num_steps), P[0, :, 6:10].T, xlabel='Row (position)',
     figsize=(6, 2.5), legend=["Col %d" % d for d in torch.arange(6, 10)])

encoding_dim, num_steps = 32, 60
pos_encoding = PositionalEncoding(encoding_dim, 0)
pos_encoding.initialize()
X = pos_encoding(np.zeros((1, num_steps, encoding_dim)))
P = pos_encoding.P[:, :X.shape[1], :]
d2l.plot(np.arange(num_steps), P[0, :, 6:10].T, xlabel='Row (position)',
     figsize=(6, 2.5), legend=["Col %d" % d for d in np.arange(6, 10)])

encoding_dim, num_steps = 32, 60
pos_encoding = PositionalEncoding(encoding_dim, 0)
params = pos_encoding.init(d2l.get_key(), jnp.zeros((1, num_steps, encoding_dim)))
X, inter_vars = pos_encoding.apply(params, jnp.zeros((1, num_steps, encoding_dim)),
                  mutable='intermediates')
P = inter_vars['intermediates']['P'][0] # retrieve intermediate value P
P = P[:, :X.shape[1], :]
d2l.plot(jnp.arange(num_steps), P[0, :, 6:10].T, xlabel='Row (position)',
     figsize=(6, 2.5), legend=["Col %d" % d for d in jnp.arange(6, 10)])

encoding_dim, num_steps = 32, 60
pos_encoding = PositionalEncoding(encoding_dim, 0)
X = pos_encoding(tf.zeros((1, num_steps, encoding_dim)), training=False)
P = pos_encoding.P[:, :X.shape[1], :]
d2l.plot(np.arange(num_steps), P[0, :, 6:10].T, xlabel='Row (position)',
     figsize=(6, 2.5), legend=["Col %d" % d for d in np.arange(6, 10)])

11.6.3.1。绝对位置信息

为了了解沿编码维度单调降低的频率与绝对位置信息的关系，让我们打印出的二进制表示0,1,…,7. 正如我们所看到的，最低位、第二低位和第三低位分别在每个数字、每两个数字和每四个数字上交替出现。

for i in range(8):
  print(f'{i} in binary is {i:>03b}')

0 in binary is 000
1 in binary is 001
2 in binary is 010
3 in binary is 011
4 in binary is 100
5 in binary is 101
6 in binary is 110
7 in binary is 111

for i in range(8):
  print(f'{i} in binary is {i:>03b}')

0 in binary is 000
1 in binary is 001
2 in binary is 010
3 in binary is 011
4 in binary is 100
5 in binary is 101
6 in binary is 110
7 in binary is 111

for i in range(8):
  print(f'{i} in binary is {i:>03b}')

0 in binary is 000
1 in binary is 001
2 in binary is 010
3 in binary is 011
4 in binary is 100
5 in binary is 101
6 in binary is 110
7 in binary is 111

for i in range(8):
  print(f'{i} in binary is {i:>03b}')

0 in binary is 000
1 in binary is 001
2 in binary is 010
3 in binary is 011
4 in binary is 100
5 in binary is 101
6 in binary is 110
7 in binary is 111

在二进制表示中，较高位的频率比较低位低。类似地，如下面的热图所示，位置编码通过使用三角函数降低编码维度上的频率。由于输出是浮点数，因此这种连续表示比二进制表示更节省空间。

P = P[0, :, :].unsqueeze(0).unsqueeze(0)
d2l.show_heatmaps(P, xlabel='Column (encoding dimension)',
         ylabel='Row (position)', figsize=(3.5, 4), cmap='Blues')

P = np.expand_dims(np.expand_dims(P[0, :, :], 0), 0)
d2l.show_heatmaps(P, xlabel='Column (encoding dimension)',
         ylabel='Row (position)', figsize=(3.5, 4), cmap='Blues')

P = jnp.expand_dims(jnp.expand_dims(P[0, :, :], axis=0), axis=0)
d2l.show_heatmaps(P, xlabel='Column (encoding dimension)',
         ylabel='Row (position)', figsize=(3.5, 4), cmap='Blues')

P = tf.expand_dims(tf.expand_dims(P[0, :, :], axis=0), axis=0)
d2l.show_heatmaps(P, xlabel='Column (encoding dimension)',
         ylabel='Row (position)', figsize=(3.5, 4), cmap='Blues')

11.6.3.2。相对位置信息

除了捕获绝对位置信息外，上述位置编码还允许模型轻松学习相对位置的注意。这是因为对于任何固定位置偏移δ, 位置的位置编码i+δ可以用位置的线性投影表示i.

这个投影可以用数学来解释。表示 ωj=1/100002j/d, 任何一对 (pi,2j,pi,2j+1)在 (11.6.2)中可以线性投影到 (pi+δ,2j,pi+δ,2j+1)对于任何固定偏移 δ:

(11.6.3)[cos⁡(δωj)sin⁡(δωj)−sin⁡(δωj)cos⁡(δωj)][pi,2jpi,2j+1]=[cos⁡(δωj)sin⁡(iωj)+sin⁡(δωj)cos⁡(iωj)−sin⁡(δωj)sin⁡(iωj)+cos⁡(δωj)cos⁡(iωj)]=[sin⁡((i+δ)ωj)cos⁡((i+δ)ωj)]=[pi+δ,2jpi+δ,2j+1],

在哪里2×2投影矩阵不依赖于任何位置索引i.

11.6.4。概括

在自我关注中，查询、键和值都来自同一个地方。CNN 和 self-attention 都享有并行计算，并且 self-attention 具有最短的最大路径长度。然而，关于序列长度的二次计算复杂度使得自注意力对于非常长的序列来说非常慢。要使用序列顺序信息，我们可以通过向输入表示添加位置编码来注入绝对或相对位置信息。

11.6.5。练习

假设我们设计了一个深度架构来表示一个序列，通过使用位置编码堆叠自注意力层。可能是什么问题？

你能设计一个可学习的位置编码方法吗？

我们能否根据在自注意力中比较的查询和键之间的不同偏移来分配不同的学习嵌入？提示：你可以参考相对位置嵌入 （Huang et al. , 2018 , Shaw et al. , 2018）。