本文我们思考这样一个问题:如何在一组逐点值的给定域上估计该域的一般函数?这种估计对于给定域上PDE数值的求解,根据扫描数据进行表面重建,或者理解采集到数据的数据结构都有所帮助。下面介绍几种常见的最小二乘法:
一、全局最小二乘估计

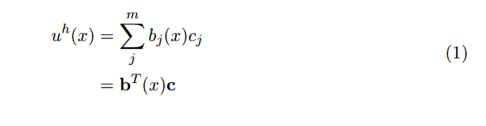

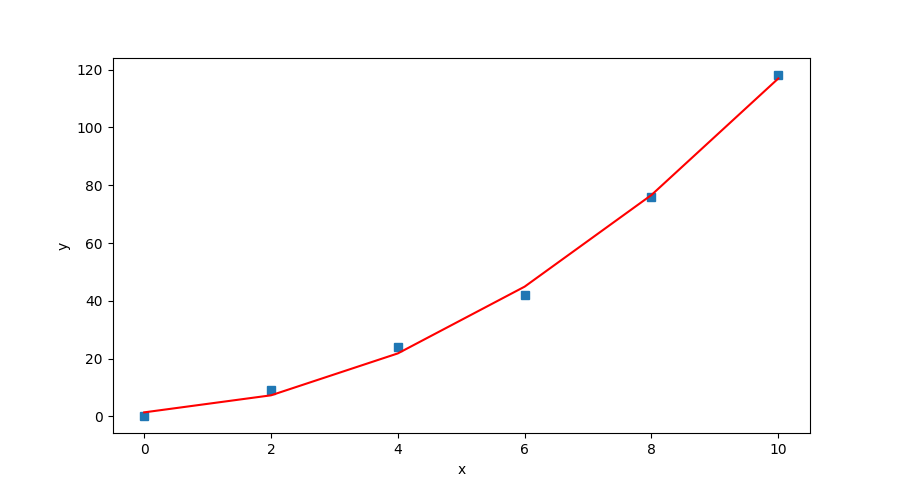
为了解决多项式拟合中的未知系数,我们构建如下的目标函数:
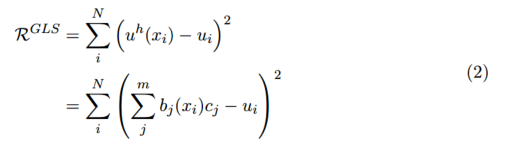
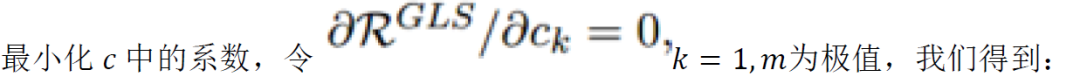
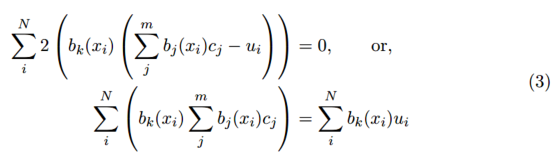
然后我们可以写个归一化方程为:
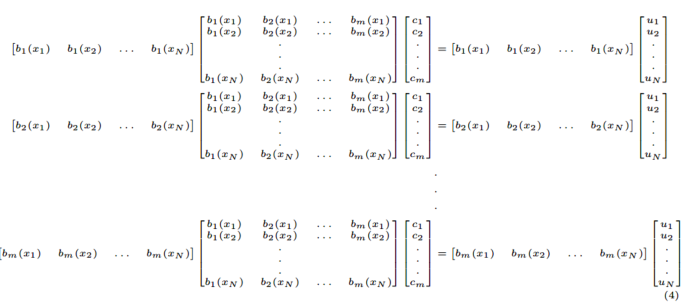
用矩阵的形式表示为:

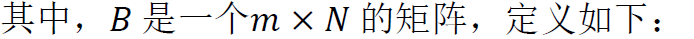
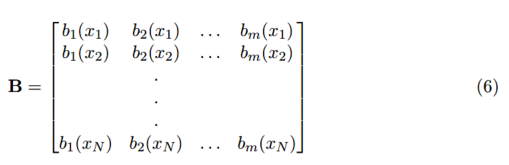
这个矩阵方程也可以直接用于计算系数向量 : 或者在大型系统中使用迭代的方法。
或者在大型系统中使用迭代的方法。
 或者在大型系统中使用迭代的方法。
或者在大型系统中使用迭代的方法。
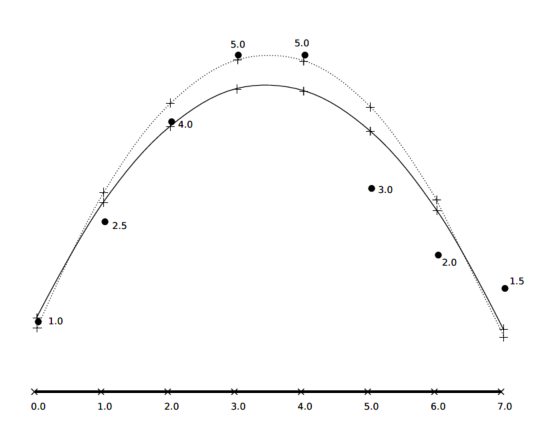
图1 全局最小二乘(实曲线)
二、全局加权最小二乘拟合
我们可以为每个数据值分配一个权重用于最小二乘拟合中,这样我们将目标函数最小化为:
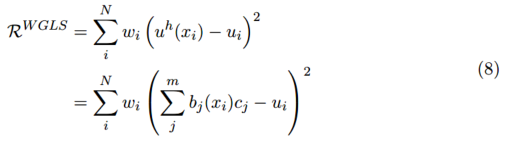
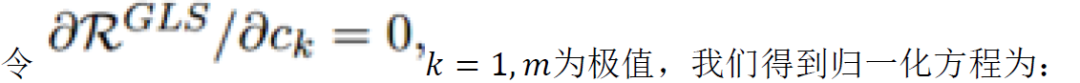
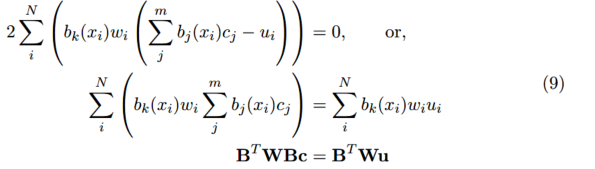

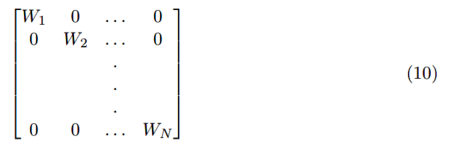
归一化方程的解为:

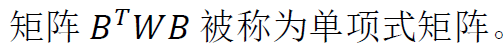
三、加权局部最小二乘
在全局最小二乘拟合中,我们假设整个域中都可以用一个单一的多项式精确地描述数据所代表的函数。但是,对于大型、复杂的数据集,这将要求我们拟合出一个不理想的高阶多项式,即便如此,这也不能捕获数据的所有特征。所以,为了替代全局解决方案,我们尝试通过对每个数据点 及其邻域拟合出一个低阶多项式来获得更好的解决方案。因此,有 个最小二乘拟合的值 ,每个值都是点 的近似值并且每个点的系数向量 都不同。注意:不同于其它讨论的方法,这不是一种公认的方法并且也不常见。它仅仅是为了我们更好的理解下一部分将要介绍的移动最小二乘法。
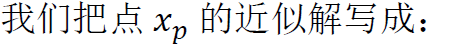
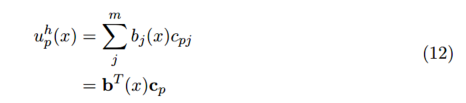

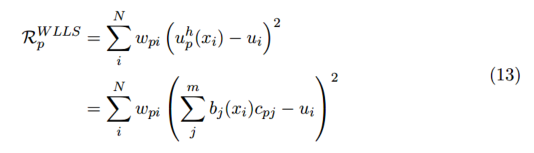

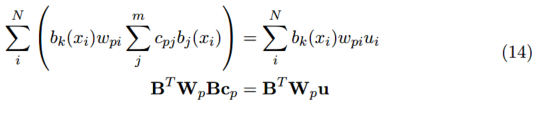
用通用的方法就可解决。



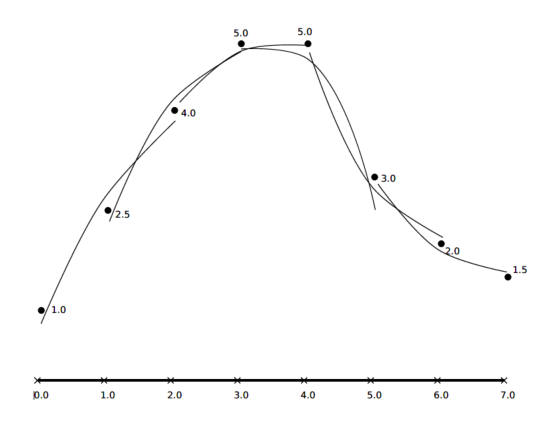
图2 加权局部最小二乘拟合
四、移动最小二乘法

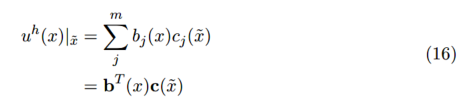

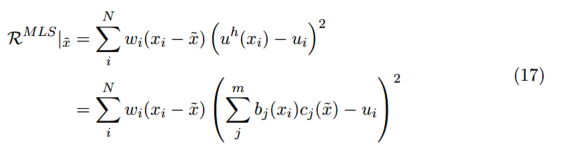

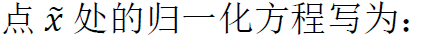
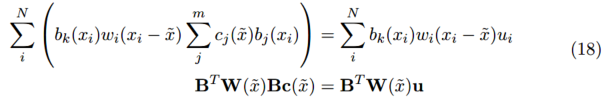

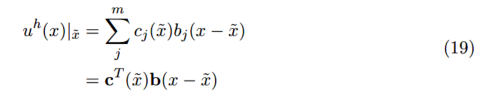

总结

声明:本文内容及配图由入驻作者撰写或者入驻合作网站授权转载。文章观点仅代表作者本人,不代表电子发烧友网立场。文章及其配图仅供工程师学习之用,如有内容侵权或者其他违规问题,请联系本站处理。
举报投诉
-
3D
+关注
关注
9文章
2875浏览量
107481 -
函数
+关注
关注
3文章
4327浏览量
62571 -
PDE
+关注
关注
0文章
4浏览量
8328
原文标题:3D曲面重建之移动最小二乘法
文章出处:【微信号:3D视觉工坊,微信公众号:3D视觉工坊】欢迎添加关注!文章转载请注明出处。
发布评论请先 登录
相关推荐
讲讲递推最小二乘法是什么
,正好沉浸下来,好好填填坑吧。1、递推最小二乘法最小二乘法最早由高斯在形体运动轨道报告研究工作中提出,此后称为参数辨识理论的基石,被广泛应用于系统辨识和参数估计之中,不得不感叹数学家们的伟大,工程技术
发表于 08-27 07:15
浅析递推最小二乘法
,正好沉浸下来,好好填填坑吧。1、递推最小二乘法最小二乘法最早由高斯在形体运动轨道报告研究工作中提出,此后称为参数辨识理论的基石,被广泛应用于系统辨识和参数估计之中,不得不感叹数学家们的伟大,工程技术
发表于 08-27 06:20
递归最小二乘法
一、递归最小二乘法递推最小二乘法:当矩阵维数增加时,矩阵求逆运算计算量过大,而且不适合在线辨识。为了减少计算量,并且可以实时地辨识出动态系统的特性,可以将最小二乘法转换成参数递推的估计。取前N组数据
发表于 08-27 07:03
最小二乘法的原理是什么
在嵌入式的测量中可能存在某些无法被直接测量的变量,但可能可以通过几个不同的数据指标运算处理得到,这里介绍最小而成发,最小二乘法适用于描述Y = AX + B的数据,即寻找到最合适的一条通过X描述Y
发表于 01-11 07:05




 3D曲面重建之移动最小二乘法
3D曲面重建之移动最小二乘法
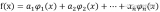










评论