什么是递归?
要说到递归如果不说栈的话,我觉得有点不合适,递归特点就是不断的调用同一个函数,如果这个函数没有一个递归界限,那么就是死循环了,所以讨论递归,就必须要讨论递归的界限,就是限定这个递归调用多少次。
我们看一个例子
#include "stdio.h"
int digui(unsigned long count )
{
if(count > 0){
count --;
printf("%d \\n",count);
digui(count);
}
return 1;
}
int main()
{
digui(10);
return (100);
}
这个递归函数的限定判读是
if(count > 0){
所以他的调用顺序可以用这个图示来说明
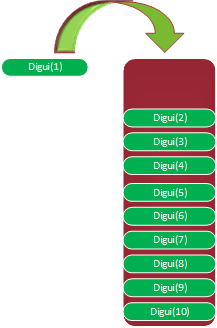
这个过程叫做递去,也就是压栈的过程,既然有压栈的过程,那么就有出栈的过程,出栈的过程就是
if(count > 0){
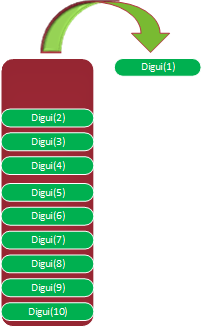
判断不成功后,就会出栈了。如下图所示
一共能执行多少次递归?
我们上面说到了,既然递归使用了栈,那么系统的栈的大小肯定是有极限的,不可能系统给你分配无极限的栈的大小,我看一些文章说栈大小是64K。
还是上面那个例子,我把传入数据设置为很大执行看看。
#include "stdio.h"
int tigui(unsigned long count )
{
if(count > 0){
count --;
printf("%d \\n",count);
tigui(count);
}
return 1;
}
int main()
{
tigui(900000);
return (100);
}
执行结果
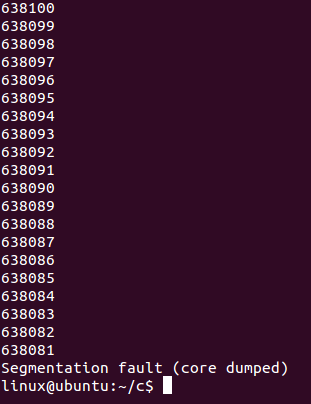
所以说递归次数肯定是有限定的了。
递归求阶乘
使用递归求阶乘是很经典的方法,我们看一下代码。
#include< stdio.h >
int fact(unsigned long n); //声明阶乘fact函数
int main(){
unsigned long x;
scanf("%d",&x);
x = fact(x);//调用函数返回int值
printf("%ld\\n",x);
return (0);
}
int fact(unsigned long n){//定义阶乘函数
if(n==1) return 1;//输入的参数是1,直接返回1
else return n*fact(n-1);//递归算法
}
执行结果
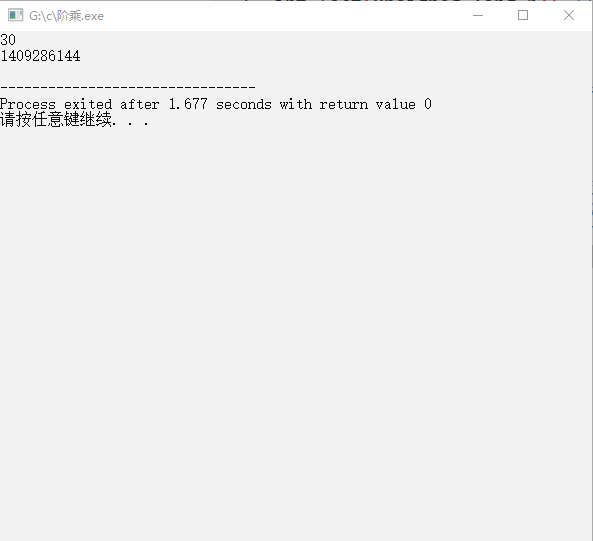
单看代码我觉得还是有点拗口 我们看个图片来看他的调用,假设我们要求的是 5 的阶乘

递归和汉诺塔
汉诺塔: 汉诺塔(又称河内塔)问题是源于印度一个古老传说的益智玩具。大梵天创造世界的时候做了三根金刚石柱子,在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定,在小圆盘上不能放大圆盘,在三根柱子之间一次只能移动一个圆盘。
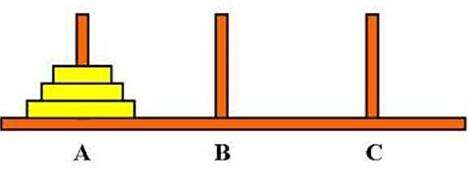
如果是这样的汉诺塔,我觉得应该每个人都觉得很简单吧,只需要三步就可以完成移动。
- 1、把小圆盘放到第三根柱子上
- 2、把中圆盘放到第二根柱子上
- 3、把小圆盘放到第二根柱子上
- 4、把大圆盘放到第三根柱子上
- 5、把小圆盘放到第一根柱子上
- 6、把中圆盘放到第三根柱子上
- 7、把小圆盘放到第三根柱子上
如图所示
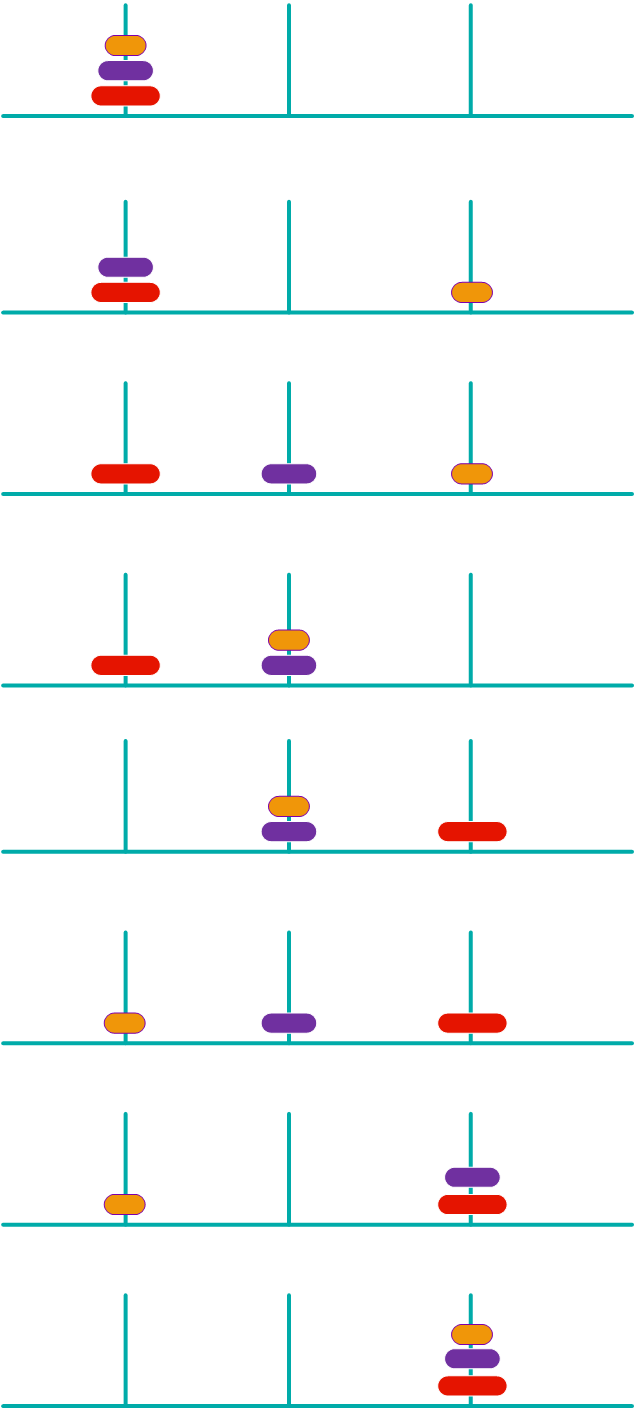
剖析我们上面是细分的方法,移动的核心思想分为三步。
- 1、把第一个柱子上的n-1圆盘移动到第二个柱子上。
- 2、把第一个柱子的第n个圆盘移动到第三个柱子上。
- 3、把第二个柱子的n-1个圆盘移动到第三个柱子。
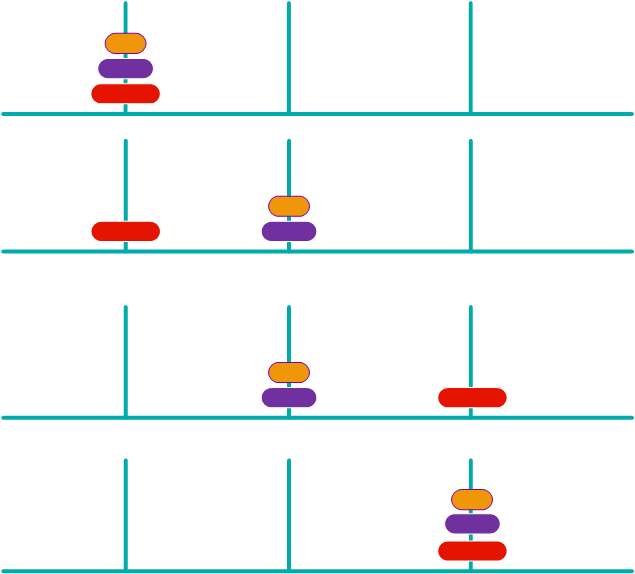
所以递归就出现了
- 1、把第一个柱子上的n-1圆盘移动到第二个柱子上「 递归实现 」。
- 2、把第一个柱子的第n个圆盘移动到第三个柱子上。
- 3、把第二个柱子的n-1个圆盘移动到第三个柱子「 递归实现 」。
C语言代码实现
#include < stdio.h >
#include < windows.h >
void Hanoi(int n, char a,char b,char c);
void Move(int n, char a, char b);
int count;
int main()
{
int n=8;
printf("汉诺塔的层数:\\n");
scanf(" %d",&n);
Hanoi(n, 'A', 'B', 'C');
printf("Exiting main...\\n");
return 0;
}
void Hanoi(int n, char a, char b, char c)
{
if (n == 1)
{
Move(n, a, c);
}
else
{
Hanoi(n - 1, a, c, b);/*把 n-1 从 a 柱子放到 b 柱子上面*/
Move(n, a, c); /*把 n 从 a 移动到 c 上*/
Hanoi(n - 1, b, a, c);/*把n - 1 通过 a 的辅助作用 从 b 移动到 c 上*/
}
}
void Move(int n, char a, char b)
{
count++;
printf("第%d次移动 Move %d: 从 %c 位置 移动到 %c !\\n",count,n,a,b);
}
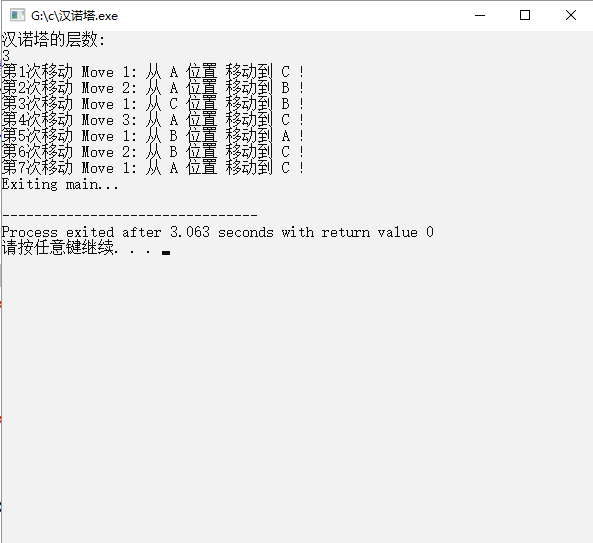
输出如图所示
加强版修改
加强了下软件写法,好好看代码,写的有点太快,没细想,后面再完善。
#include < stdio.h >
/*柔性数组*/
typedef struct _soft_array{
int len;
int array[];
}soft_array;
/*汉诺塔结构体*/
typedef struct _hannuo{
soft_array *p_data;
char name;
}hannuo;
hannuo * han_a = NULL;
hannuo * han_b = NULL;
hannuo * han_c = NULL;
void hannoiii(int n,hannuo * a,hannuo * b,hannuo * c);
void moveiii (int n,hannuo * a,hannuo * c);
int total;
void printf_han_data(hannuo * han)
{
int i = 0;
printf("%c: ",han- >name);
/*输出汉诺塔的数据*/
for(i = 0;i< han- >p_data- >len;i++)
{
printf("%d-",han- >p_data- >array[i]);
}
printf("\\n");
}
int main()
{
int i = 0;
int n = 0;
scanf(" %d",&n);
total = n;
/*定义三个汉诺塔节点*/
han_a = (hannuo *)malloc(sizeof(hannuo));
han_a- >name = 'A';
han_a- >p_data = (soft_array*)malloc(sizeof(soft_array)+sizeof(int)*n);
han_a- >p_data- >len = n;
/*数据原来在第一根柱子上*/
for(i = 0;i< n;i++)
{
han_a- >p_data- >array[i] = i+1;
}
printf_han_data(han_a);
/*初始化第二根柱子*/
han_b = (hannuo *)malloc(sizeof(hannuo));
han_b- >name = 'B';
han_b- >p_data = (soft_array*)malloc(sizeof(soft_array)+sizeof(int)*n);
memset(han_b- >p_data,0,sizeof(soft_array)+sizeof(int)*n);
han_b- >p_data- >len = n;
printf_han_data(han_b);
/*初始化第三根柱子*/
han_c = (hannuo *)malloc(sizeof(hannuo));
han_c- >name = 'C';
han_c- >p_data = (soft_array*)malloc(sizeof(soft_array)+sizeof(int)*n);
memset(han_c- >p_data,0,sizeof(soft_array)+sizeof(int)*n);
han_c- >p_data- >len = n;
printf_han_data(han_c);
printf("------------------------\\n");
hannoiii(n,han_a,han_b,han_c);
printf("\\n");
return 0;
}
void hannoiii(int n,hannuo * a,hannuo * b,hannuo * c)
{
if(n == 1)
{
a- >p_data- >array[



 C语言,你真的懂递归了吗?
C语言,你真的懂递归了吗?