Peter Delos, Sam Ringwood, 和 Michael Jones
相控阵校准工作通常侧重于优化目标基波信号。本文介绍了一种在已知所需信号的相位校准后进一步提高杂散性能的方法。使用这种方法,我们将评估由四个32元素子阵列组成的8元素混合波束成形系统上的传输杂散信号。所示测量结果显示性能改进超过 25 dB。为了扩展到更大的系统,我们考虑了何时适用消除方法与确保杂散信号不相关的方法。
介绍
对于未来的相控阵,行业对软件定义天线有着重要的追求。这带来了对全数字相控阵的强烈需求,以最大限度地提高天线方向图可编程性。在实践中,特别是随着频率的增加,封装、功耗和数字处理方面的挑战迫使数字通道数量减少。混合波束成形提供了实现工程师通常需要的数字信道密度缓解,因此在未来一段时间内可能会成为一种实用的选择。
在大型数字波束成形天线中,无论混合波束成形与数字波束成形的架构如何,通过组合来自分布式波形发生器和接收器的信号的波束成形过程来提高动态范围是非常可取的。如果相关的误差项不相关,则可以在噪声和杂散性能方面获得10logN的动态范围改进。在这种情况下,N 是波形发生器或接收器通道的数量。噪声本质上是一个随机过程,因此非常适合跟踪相关和不相关的噪声源。然而,强制杂散信号不相关不太明显。因此,任何可能迫使杂散信号不相关的设计方法对相控阵系统设计人员来说都是有价值的。
在相控阵中强制杂散去相关的各种方法已经为人所知。我们最早的出版物可追溯到2002年,2其中描述了确保接收器杂散信号不相关的通用方法。在该方法中,信号首先以已知方式在两个接收器上修改。然后信号被接收器的非线性分量失真。在接收器输出端,接收器中先前引入的修改是反转的。预期的信号变得相干或相关,但扭曲的项不相关。Howard(2002)中实现的修改方法是将每个本地振荡器(LO)合成器设置为不同的频率,然后通过在数字处理中对数控振荡器(NCO)进行数字调谐来校正修改。多年来还发表了其他几种方法。3,4最近证明了抵消LO频率的方法,并在基于商用集成收发器的设计的测试结果中证明是有效的。5,6最近,已经公布了有关分布式直接采样RF数据转换器的杂散改进的数据。7,8
在这项工作中,我们表明,在信道匹配良好且特定杂散频率在通道之间固有相关的情况下,混合波束成形架构有助于提供一种方法,不仅可以强制杂散信号不相关,还可以通过消除方法得到更显着的改进。我们还表明,消除可以嵌入到校准中,作为阵列中相位校准之后的第二步。
为了说明该方法的价值,我们介绍了图1。在这里,测量显示仅四个数字子阵列的SFDR改进>25 dB。请注意,初始主导杂散明显低于其他杂散信号。由于不相关的噪声或杂散信号,仅四个通道的这种幅度的杂散改善远远超过标准的10logN改善,并且已经证明了杂散信号的消除。
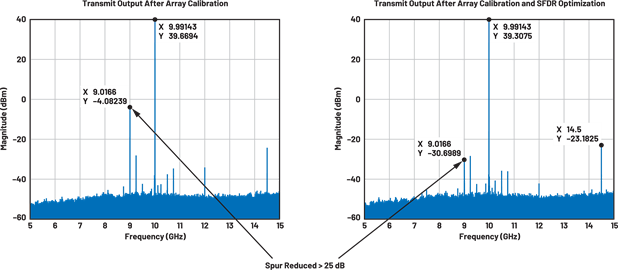
图1.发射输出的频谱。在相控阵校准之后显示在左侧,而在附加SFDR优化校准之后显示在右侧。
组合噪声电压
当信号在自由空间或RF组合中组合时,每个信号的噪声增加为
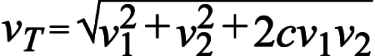
C 范围 –1 至 +1
–1 -> 取消
0 -> 不相关
+1 -> 完全相关
杂散可以视为噪声电压
对于相控阵,RF性能的一般目标是相关系数为0。这导致阵列级动态范围改进了 10logN,其中 N 是通道数。在某些特定情况下,c可以是负数并且可以创建取消,在这项工作中,我们演示了一个可以应用取消的示例。
考虑是否发现特定的混频杂散跨通道相关。在这种情况下,相关意味着混频杂散信号在幅度和相位上跨通道匹配。如果存在这种情况,则混合波束成形架构固有地提供钩子,通过在直接数字频率合成器(DDS)和模拟波束成形集成电路(BFIC)移相器上找到最佳的相位旋转来消除杂散。
硬件演示器说明
已经开发出32单元混合波束成形原型平台,9详细的信号链如图2所示。
前端由 32 个发送/接收模块和 8 个模拟 BFIC 组成。两个 BFIC 输入/输出组合产生四个 4 元素子阵列。四个子阵列连接到一个 4 通道微波上变频器/下变频器。然后,4通道微波上变频器/下变频器连接到包含四个模数转换器(ADC)和四个数模转换器(DAC)的数字化仪IC。ADC的采样速率为12 GSPS,而DAC的采样速率为<> GSPS。
表征的微波频率为8 GHz至12 GHz。LO设置为以4.5 GHz为中心的固定中频(IF)的高边LO。在此IF频率下,ADC在第三个奈奎斯特区采样。
商用FPGA板用于数据采集。已经开发了MATLAB计算机控制接口,可以在实际硬件中快速表征波形。数据分析在 MATLAB 中进行后处理。®
强制杂散相位旋转
考虑图1所示的杂散电平。具体的杂散和以dBc为单位的杂散电平如表1所示。显示了每个子阵列的杂散电平,初始校准后的整个阵列以及额外SFDR校准后的整个阵列。
| 杂散积 | 子阵列 1 (dBc) | 子阵列 2 (dBc) | 子阵列 3 (dBc) | 子阵列 4 (dBc) | 全阵列 (dBc) 后阵列校准 | 全阵列 (dBc) SFDR 优化后 |
| 2中频 | –43.6 | –46.1 | –43.8 | –41.7 | –43.7 | –70 |
| LO 泄漏 | –50.1 | –55.4 | –58.1 | –52.2 | –64.1 | –62.5 |
| 数字转换器时钟 | –68.7 | –66.8 | –69.2 | –65.1 | –71.9 | –81.7 |
|
轨道 1 (9.24 GHz) |
–67.1 | –68.2 | –64.3 | –65.5 | –67.9 | –67.9 |
|
轨道 2 (10.5 GHz) |
–72.5 | 73.3 | –72.9 | –74.8 | –77.3 | –75.3 |
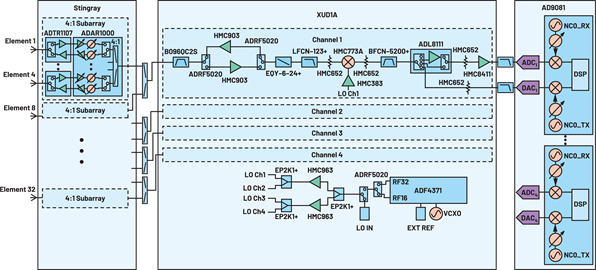
图2.X波段混合波束成形演示框图。
请注意,在此数据中,2IF 杂散在每个子阵列中处于同一级别。全阵列校准后,组合数据显示2IF杂散处于相同dBc电平,没有改善。这表明2IF杂散在通道之间是相关的。这就带来了一个问题,“如果杂散是相关的,那么马刺可以被迫不相关吗?第二个问题变成了,“如果马刺如此相关,那么他们是否可以被迫被取消?
图3示出了在保持基波RF信号相位的同时可视化旋转2IF杂散相位的方法。
首先,假设基波和2IF杂散都在0°处同相对齐。
如果中频频率的相位旋转相位θ,则2IF频率将以该速率的两倍或2θ旋转。这可以通过NCO或基带IQ数据的DAC输出相位来控制。
此架构中使用了高端LO。这会导致RF相位以与IF相位相反的方向旋转,从而使RF相位旋转–θ。这意味着子阵列的模拟BFIC移相器都需要旋转θ以重新对齐基频。模拟移相器的这种偏移导致2IF杂散上的额外θ相移,总相移为3θ。
图3显示了2IF杂散可以旋转的原理。期望的结果是在每个子阵列上找到适当的旋转,以便在发射输出端消除2IF杂散。我们将展示混合波束成形相控阵架构提供了DDS频率生成时的IF相位控制和通过子阵列模拟BFIC的RF相位控制的必要组合,以实现内置机制在子阵列之间旋转2IF杂散的相对相位。
发射校准
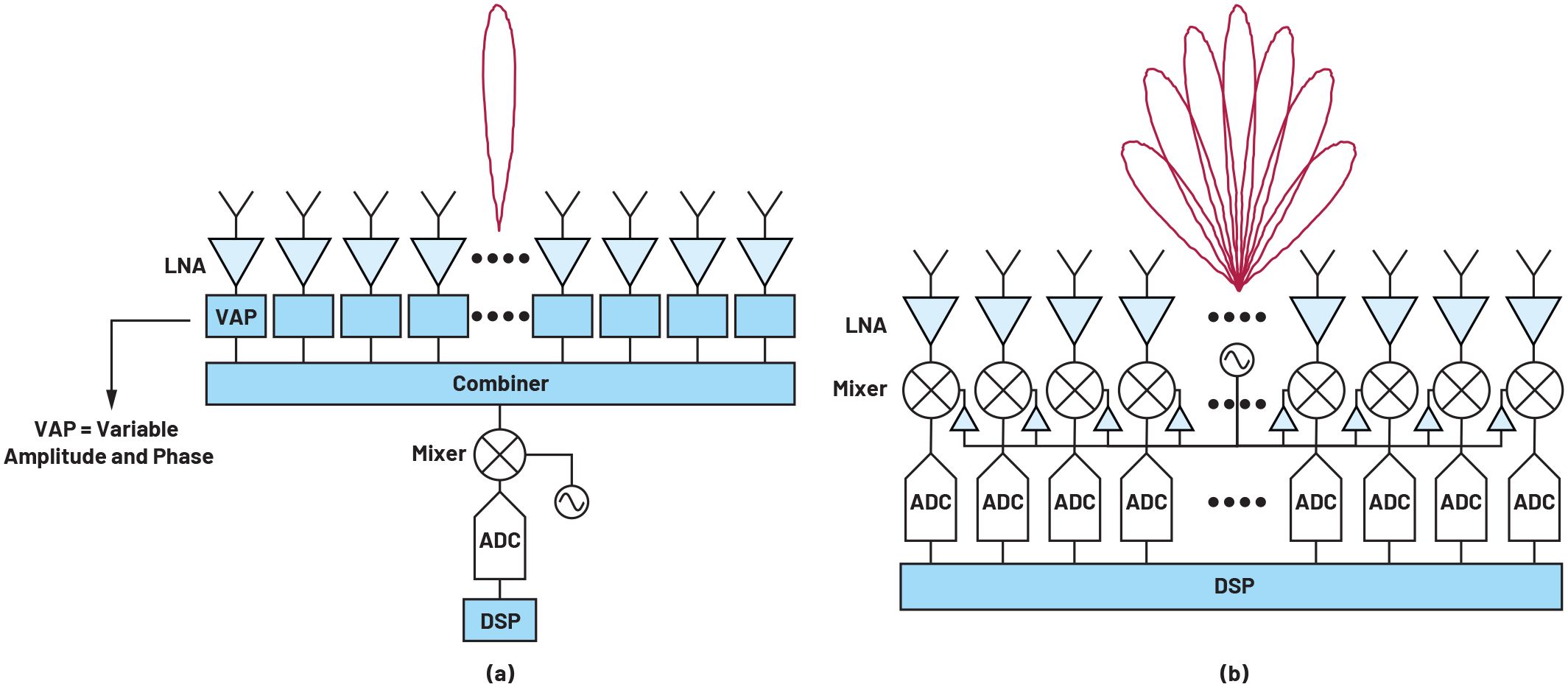
图4显示了通用的混合波束成形架构,并在Delos研究中进行了进一步描述。8图4还突出显示了天线校准中使用的可编程幅度和相位控制。
本文讨论了用于对齐硬件幅度和相位的校准步骤。
振幅校准
测量每个通道的信号幅度,并将其均衡到功率最低的通道。为了同时测量各个子阵列,频率间隔开,以便从单个频谱分析仪测量中测量每个子阵列。
相位校准
为了实现跨子阵列的同时捕获,采用了时间交错脉冲校准方法。脉冲是每个子阵列的时间交错。脉冲连续波(CW)信号被施加到频谱分析仪设置中,以卸载同相(I)和正交相位(Q)数据。频谱分析仪在 IQ 数据模式下能够提供 160 MHz 带宽。发射中心频率与频谱分析仪中心频率偏移 8 MHz,以观察 IQ 数据中的完整周期。根据这些数据,子阵列中的相位是匹配的。此概念如图 5 所示。
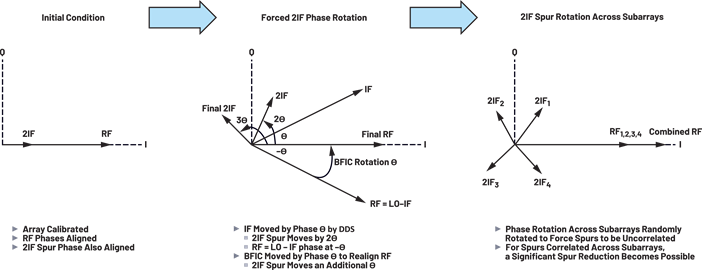
图3.强制2IF杂散相位旋转。
实现的相位对齐步骤如下:
第 1 步:在所有四个子阵列中对齐元素 1。
这是通过单个数据捕获实现的,使用时间交错脉冲对每个子阵列启用元素 1 并禁用其他元素。
步骤 2:对齐子数组 2、8 和 2 中的元素 3 到 4。
这是通过七个脉冲数据采集来实现的。在每个数据捕获中,第一个脉冲来自子阵列 1 元素 1,其余三个脉冲用于子阵列 2、3 和 4,每个数据捕获通过元素 2 到 8。
步骤 3:对齐子阵列 2 中的元素 8 到 1。
这是通过七个2脉冲数据捕获来实现的。在每个数据捕获中,第二个脉冲是子阵列 2 元素 1,第一个脉冲步进子阵列 1 元件 2 到 8。
SFDR 优化
2IF杂散相位旋转的原理在强制杂散相位旋转部分进行了概述。接下来,我们将其映射到方程表示中,以便更轻松地转换为用于校准的软件脚本。
首先,我们介绍使用的符号:

发射校准中描述的阵列校准后每个元件的输出相位可以写为:

引入额外的SFDR相位优化项,在阵列校准和SFDR优化步骤之后,每个元件的所需信号相位可以写成:

同样,此SFDR相位优化步骤导致2IF杂散的每个元件的输出相位,可写为:

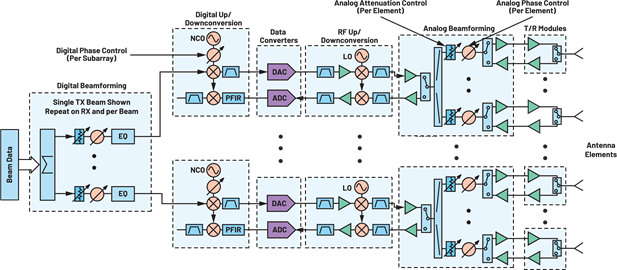
图4.一种通用的混合波束成形架构,概述了用于天线校准的幅度和相位可编程控制。
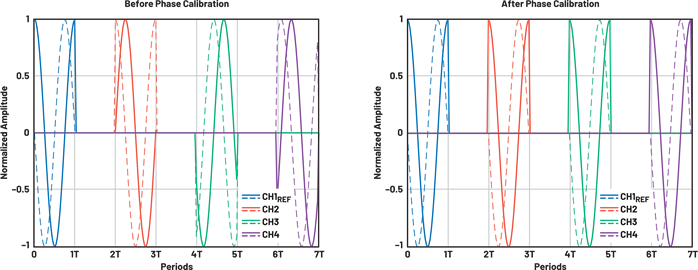
图5.时间交错脉冲校准用于确定通道间的相位误差。
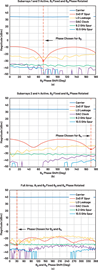
图6.(a) SFDR 优化步骤 1:子阵列 1 和 3 处于活动状态:θ1= 0, i3从0°旋转到180°;(b) SFDR 优化步骤 2:子阵列 2 和 4 处于活动状态:θ2= 0, i4从0°旋转到180°;(c) SFDR 优化步骤 3:所有子阵列都处于活动状态:θ3和 θ4固定在从步骤 1 和 2 中选择的相位,θ2和 θ4从 0° 旋转到 360°。
SFDR 优化分三个步骤完成,如图 6 所示。第一步包括激活阵列的一半,并将一个子阵列的模拟和数字相位从0°旋转到180°,同时将另一个相位固定在0°。在这种情况下,子数组 1 和 3 处于活动状态,而 θ1固定在 0° 和 θ3在关注 2IF 杂散大小的同时旋转。图6a显示了θ3在此限度下,2IF杂散最小值。优化步骤 2 的执行方式与步骤 1 类似,但不同的子阵列处于活动状态。对于步骤 2,子数组 2 和 4 处于活动状态,而 θ2固定在 0° 和 θ4被旋转。θ 的确定相位偏移4是当2IF杂散幅度处于最小值时,如图6b所示。
最后,在所有子阵列处于活动状态时应用步骤 1 和 2 中的优化相位偏移,并在两个子阵列上执行最终相位旋转。图6c显示了θ1和 θ3保持在固定值,而 θ2和 θ4被旋转。同样,最佳相位偏移是2IF杂散幅度的相应最小值。值得澄清最终的θ4值是在步骤 2 和 3 中选择的相位偏移的总和。
跨带宽验证
每当实施取消时,一个问题是验证跨带宽和其他条件的取消保留。在所使用的硬件演示器中,需要考虑三个方面:基带IQ数据到数字化仪IC的调制,DAC数字上变频器中NCO频率的变化以及LO频率的变化。这些结果如图 7 所示。IQ 数据在 100 MHz 范围内变化,NCO 频率在 500 MHz 范围内变化,LO 在 2 GHz 范围内变化。在所有情况下,与未实施SFDR优化相比,2IF杂散保持显着降低的水平。
杂散取消与强制杂散不相关
关于杂散消除与更简单的去相关方法以及对大型相控阵系统的适用性的观点值得讨论。
在此硬件的情况下,我们演示了一种杂散消除方法。如果关注的杂散显示在整个阵列中相关,则可以将其应用于单个显性杂散。如果将数组分区为较小的子数组组以进行 SFDR 优化,或者我们的方法可以通过将数组拆分为象限来按原样使用,则可以将我们描述的优化扩展到更大的数组。
有许多支线很难取消。在这种情况下,确保杂散信号不相关的10logN改进更为实用。对于许多幅度不匹配的杂散或杂散的情况,可以在整个阵列中使用优化步骤期间的SFDR相位随机化,以确保杂散信号不相关,并且仍然可以通过这种相对简单的软件级实现提供改进。
未来工作
对于相控阵,尚未讨论的考虑因素是SFDR在远离主传输光束时的影响。在校准和SFDR优化步骤之后,当主信号全部相干或朝向主光束方向时,将应用杂散减少。在偏角处,主载体和杂散都存在相位旋转。用于减少主光束方向上的SFDR的SFDR优化可能导致杂散在其他角度方向上相位对齐。将评估这一效果,作为这项工作的后续行动。
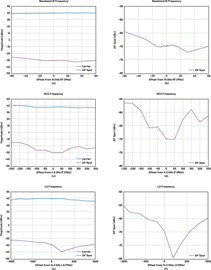
图7.显示了三个可编程选项的频率扫描结果:DDS频率、NCO频率和LO频率;(a) DDS频率扫描的载波幅度和2IF杂散幅度;(b) DDS频率扫描的2IF杂散dBc电平;(c) NCO频率扫描的载波幅度和2IF杂散幅度;(d) 用于NCO频率扫描的2IF杂散dBc电平;(e) LO频率扫描的载波幅度和2IF杂散幅度;(f) LO频率扫描的2IF杂散dBc电平。
结论
混合波束成形相控阵架构具有天然的钩子,可以迫使混杂杂散不相关。该架构在波束成形IC的模拟移相器中提供相移控制,在数字域中提供相位控制,可通过基带数据或NCO相位调整实现。这些两相控制元件的组合直接在架构中提供了嵌入式相位控制,作为相控阵校准第一级之后的第二步,可以利用这些控制来优化SFDR性能。我们已经在商用硬件上演示了这种能力,描述了优化步骤,并提供了测量结果。
审核编辑:郭婷
-
嵌入式
+关注
关注
5068文章
19008浏览量
302965 -
dac
+关注
关注
43文章
2268浏览量
190819 -
NCO
+关注
关注
0文章
22浏览量
24652
发布评论请先 登录
相关推荐
毫米波波束成形和天线设计
雷达模拟波束成形和数字波束成形的区别
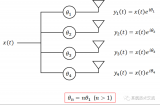
一种波束成形系统的相位测量方法介绍
【模拟对话】相控阵波束成形IC简化天线设计
MIMO信道多用户块传输SCFDE系统的联合波束成形
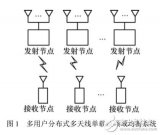
无线网络中功率分配的安全波束成形
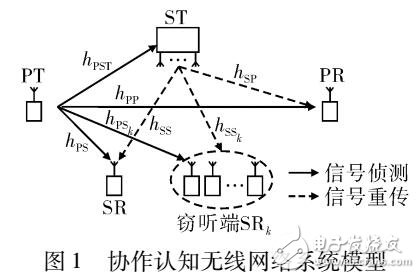
波束成形的类型及其在RF PCB中的用途
毫米波波束成形和天线技术的实例说明
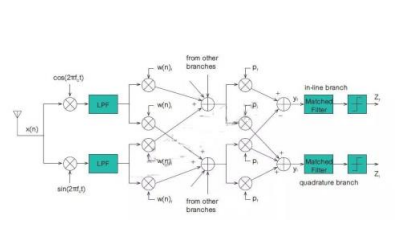
混合波束成形接收机动态范围理论实践
如何实现毫米波波束成形和大规模MiMo?





 采用SFDR优化的混合波束成形发射校准
采用SFDR优化的混合波束成形发射校准











评论