
点击上方蓝字关注我们
高性能浮点处理一直与高性能CPU相关联。在过去几年中,GPU也成为功能强大的浮点处理平台,超越了图形,称为GP-GPU(通用图形处理单元)。新创新是在苛刻的应用中实现基于FPGA的浮点处理。本文的重点是FPGA及其浮点性能和设计流程,以及OpenCL的使用,这是高性能浮点计算前沿的编程语言。
各种处理平台的GFLOP指标在不断提高,现在,TFLOP/s这一术语已经使用的非常广泛了。但是,在某些平台上,峰值GFLOP/s,即,TFLOP/s表示的器件性能信息有限。它只表示了每秒能够完成的理论浮点加法或者乘法总数。分析表明,FPGA单精度浮点处理能够超过1 TFLOP/s。
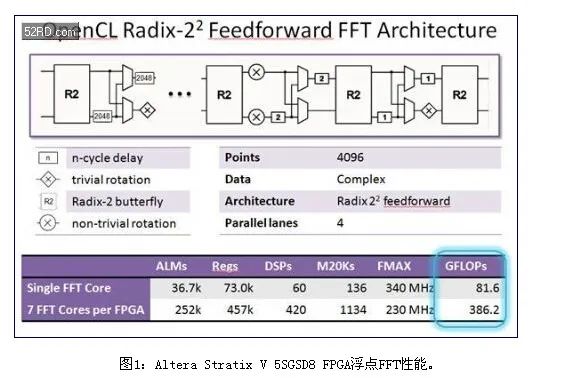
一种不太复杂的常用算法是FFT。使用单精度浮点实现了4096点FFT。它能够在每个时钟周期输入输出四个复数采样。每一个FFT内核运行速度超过80 GFLOP/s,大容量FPGA的资源支持实现7个这类的内核。
但是,如图1所示,这一FPGA的FFT算法GFLOP/s接近400 GFLOP/s。这是“按键式”OpenCL编译结果,不需要FPGA知识。使用逻辑锁定和DSE进行优化,7内核设计接近单内核设计的Fmax,将其GFLOP/s提升至500,超过了10 GFLOP/s每瓦。
这一每瓦GFLOP/s要比CPU或者GPU功效高很多。对比一下GPU,GPU在这些FFT长度上效率并不高,因此,没有进行基准测试。当FFT长度达到几十万个点时,GPU效率才比较高,能够为CPU提供有效的加速功能。
总之,实际的GFLOP/s一般只达到峰值或者理论GFLOP/s的一小部分。出于这一原因,更好的方法是采用算法来对比性能,这种算法能够合理的表示典型应用的特性。算法越复杂,典型实际应用的基准测试就越具有代表性。
并不是依靠供应商的峰值GFLOP/s指标来确定处理技术,而是使用比较复杂具有代表性的第三方评估。高性能计算理想的算法是Cholesky分解。
这一算法经常用于线性代数,高效的解出多个方程,可以实现矩阵求逆功能。这一算法非常复杂,要获得合理的结果总是要求浮点数值表示。计算需求与N3成正比,N是矩阵维度,因此,一般对处理要求很高。实际GFLOP/s取决于矩阵大小以及所要求的矩阵处理吞吐量。
表1显示了基于Nvidia GPU指标1.35TFLOP/s的基准测试结果,使用了各种库,以及Xilinx Virtex6 XC6VSX475T,其密度达到475K LC,这种FPGA针对DSP处理进行了优化。用于Cholesky基准测试时,这些器件在密度上与AlteraFPGA相似。
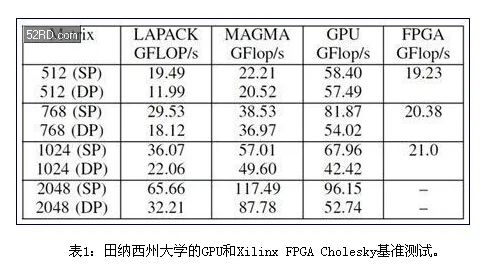
LAPACK和MAGMA是商用库,而GPU GFLOP/s是指采用田纳西州大学开发的OpenCL实现的。对于小规模矩阵,后者更优化一些。
中等规模的Altera Stratix V FPGA (460kLE)也进行了基准测试,使用了单精度浮点Cholesky算法。如表2所示,在Stratix V FPGA上进行Cholesky算法的性能要比Xilinx结果高很多。
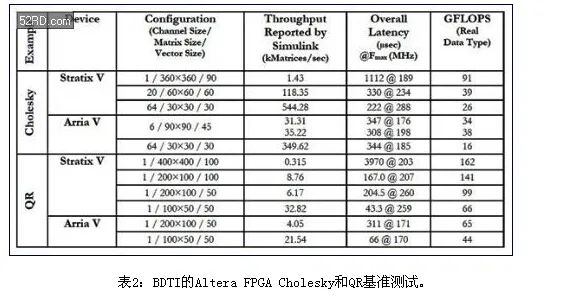
应指出,矩阵大小并不相同。田纳西州大学结果是从[512×512]矩阵大小开始的。BDTI基准测试达到了[360×360]矩阵大小。原因是,矩阵规模较小时,GPU效率非常低,因此,在这些应用中,不应该使用它们来加速CPU。在规模较小的矩阵时,FPGA的工作效率非常高。
其次,BDTI基准测试是基于每个Cholesky内核的。每个可参数赋值的Cholesky内核支持选择矩阵大小,矢量大小和通道数量。矢量大小大致决定了FPGA资源。较大的[360×360]矩阵使用了较长的矢量,支持这一FPGA中实现一个内核,达到91GFLOP/s。较小的[60×60]矩阵使用的资源更少,因此,可以实现两个内核,总共是2×39=78GFLOP/s。的[30×30]矩阵支持实现三个内核,总共是3×26=78GFLOP/s。
FPGA看起来更适合解决数据规模较小的问题。原因之一是因为计算负载随N3而增大,数据I/O随N2增大,终,随着数据的增加,GPU的I/O瓶颈不再是问题。另一项考虑是吞吐量。随着矩阵规模的增大,由于每个矩阵的处理量增大,矩阵每秒吞吐量会大幅度下降。在某些点,吞吐量变得非常低,以至于无法满足很多应用的要求。在很多情况下,会分解大规模矩阵,处理每个小的子矩阵,以解决由于庞大的处理负载造成的吞吐量限制问题。
对于FFT,计算负载增加N log2 N,而数据I/O随N增大而增大。对于规模较大的数据,GPU是高效的计算引擎。作为对比,数据长度很短时,FPGA是高效的计算引擎,更适合FFT长度达到数千的很多应用,对于GPU,FFT长度是数十万。
GPU和FPGA设计方法
使用Nvidia的专用CUDA语言或者开放标准OpenCL语言对GPU进行编程。这些语言在能力上非常相似,而的不同在于CUDA只能用在Nvidia GPU上。
FPGA通常使用HDL语言Verilog或者VHDL进行编程。这些语言的版虽然采用了浮点数定义,不用进行综合,但都不太适合支持浮点设计。例如,在System Verilog中,短实数变量与IEEE单精度(浮点)对应,实数变量与IEEE双精度对应。
使用传统的方法,将浮点数据通路综合到FPGA的效率非常低。Xilinx FPGA在Cholesky算法上的性能很低,它使用了Xilinx浮点内核生成功能,这证实了这一点。而Altera采用了两种不同的方法。种使用基于Mathworks的设计输入,称之为DSP Builder模块库。这一工具包含了对定点和浮点数的支持。它支持7种不同精度的浮点,包括IEEE半精度、单精度和双精度。它还支持矢量化,这是高效实现线性代数所需要的。而重要的是,它能够将浮点电路高效的映射到目前的定点FPGA体系结构中,如基准测试所示,规模中等的28 nm FPGA,Cholesky算法接近了100GFLOP/s。作为对比,在不具有综合能力的规模相似的Xilinx FPGA上,实现同样的算法,使用密度相似的FPGA,性能只有20GFLOP/s。
GPU编程人员比较熟悉OpenCL。面向FPGA的OpenCL编译意味着,面向AMD或者Nvidia GPU编写的OpenCL代码可以编译到FPGA中。Altera的OpenCL编译器支持GPU程序使用FPGA,不需要熟练的开发典型的FPGA设计。
使用支持FPGA的OpenCL,相对于GPU有几个关键优势。首先,GPU的I/O是有限制的。所有输入和输出数据必须由主CPU通过PCI接口进行传输。结果延时会让GPU处理引擎暂停,因此,降低了性能。
FPGA以各种宽带I/O功能而。这些功能支持数据通过千兆以太网和SRIO,或者直接从ADC和DAC输入输出FPGA。Altera定义了OpenCL标准的供应商专用扩展,以支持流操作。
即使与I/O瓶颈无关,FPGA的处理延时也要比GPU低很多。众所周知,GPU必须有数千个线程才能高效的工作。这是由于存储器读取很长的延时,以及GPU大量的处理内核之间的延时。实际上,GPU必须有很多任务才能使得处理内核不会暂停等待数据,否则会导致任务很长的延时。
而FPGA使用了“粗粒度并行”体系结构。它建立了多个经过优化的并行数据通路,每一通路一般在每个时钟周期输出一个结果。数据通路的例化数取决于FPGA资源,但一般要比GPU内核数少很多。但是,每一数据通路例化的吞吐量要比GPU内核高得多。这一方法的主要优势是低延时。降低延时在很多应用中都是关键的性能优势。
FPGA的另一优势是很低的功耗,极大的降低了每瓦GFLOP/s。正如BDTI所测量的,Cholesky等复数浮点算法的每瓦GFLOP/s是每瓦5~6GFLOP/s。一般很难进行GPU能效测量,但是,Cholesky的GPU性能达到50GFLOP/s,典型功耗是200W,得到的结果是0.25每瓦GFLOP/s,单位FLOP/s的功率高20倍。
OpenCL和DSP Builder都依靠“融合数据通路”这种技术(图2),以这种技术实现浮点处理,能够大幅度减少桶形移位电路,从而支持使用FPGA来开发大规模高性能浮点设计。
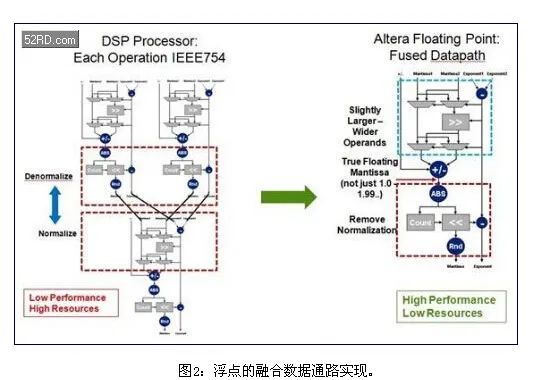
为降低桶形移位频率,综合过程尽可能使用较大的尾数宽度,从而不需要频率归一化和去归一化。27×27和36×36硬核乘法器支持比单精度实现所要求的23位更大的乘法计算,54×54和72×72结构的乘法器支持比52位更大的计算,这通常是双精度实现所要求的。FPGA逻辑已经针对大规模定点加法器电路进行了优化,包括了内置进位超前电路。
当需要进行归一化和去归一化时,另一种可以避免低性能和过度布线的方法是使用乘法器。对于一个24位单精度尾数(包括符号位),24×24乘法器通过乘以2n对输入移位。27×27和36×36硬核乘法器支持单精度扩展尾数,可以用于构建双精度乘法器。
在很多线性代数算法中,矢量点乘(图3)是占用大量FLOP/s的底层运算。单精度实现长度是64的长矢量点乘需要64个浮点乘法器,以及随后由63个浮点加法器构成的加法树。这类实现需要很多桶形移位电路。
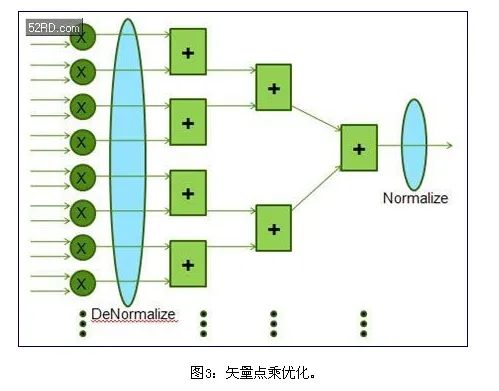
相反,可以对64个乘法器的输出进行去归一化,成为公共指数,是64位指数。可以使用定点加法器电路对这些64路输出求和,在加法树的进行终的归一化。如图3所示,这一本地模块浮点处理过程省掉了每一加法器所需要的临时归一化和去归一化。即使是IEEE754浮点,指数基本决定了终的指数,因此,这种改变只是在计算早期进行指数调整。
但是,进行信号处理时,在计算尽可能以高精度来截断结果才能获得结果。这种方法进位额外的尾数,补偿了单精度浮点处理所需要的早期去归一化次优方法,一般从27位到36位。采用浮点乘法器进行尾数扩展,因此,在每一步不需要对乘积进行归一化。
注意,这一方法每个时钟周期也会产生一个结果。GPU体系结构可以并行产生所有浮点乘法,但是不能高效的并行进行加法。之所以这样是因为不同的内核必须通过本地存储器传输数据,彼此实现通信,因此,不能灵活的连接FPGA体系结构。
这一方法产生的结果要比传统IEEE754浮点结果得多,如表3的测量结果所示。BDTI的基准测试获得了相似的结果。
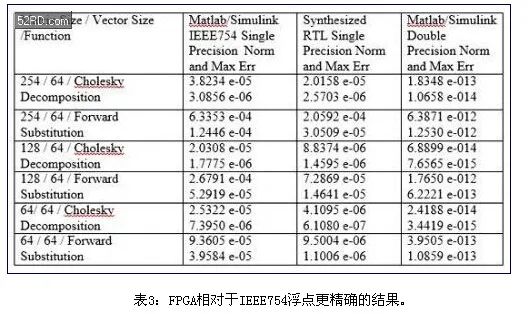
使用Cholesky分解算法,实现大规模矩阵求逆,获得了表3的结果。以三种不同的方法实现了相同的算法——在Matlab/Simulink中,使用了IEEE754单精度浮点,在RTL单精度浮点处理中,使用融合数据通路方法,在Matlab中也使用了双精度浮点。双精度实现要比单精度实现精度高十亿倍(109)。
表3对比了Matlab单精度;RTL单精度和Matlab双精度存在误差,确认了融合数据通路方法的完整性。采用了这一方法来获得输出矩阵中所有复数元素的归一化误差以及矩阵元素的误差。使用Frobenius范数计算了总误差和范数:
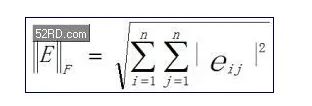
请注意,由于范数包括了所有元素的误差,因此,它要比每一误差大很多。
而且,DSP Builder模块库和OpenCL工具流程都针对下一代FPGA体系结构,支持并优化目前的设计。由于体系结构创新和工艺技术创新,性能可以达到100峰值GFLOPs/W。
总结
高性能计算应用现在有新的处理平台选择。对于特殊类型的浮点算法,FPGA能够提供低延时和较高的GFLOP/s。在几乎所有应用中,FPGA都能够实现优异的每瓦GFLOP/s。随着下一代高性能计算优化FPGA的推出,这种优势会更明显。
Altera的OpenCL编译器为GPU编程人员提供了几乎无缝的方法来评估这一新处理体系结构的指标。Altera OpenCL符合1.2规范,提供全面的数据库支持。它解决了传统FPGA遇到的时序收敛、DDR存储器管理以及PCIe主处理器接口等难题。
对于非GPU开发人员,Altera提供DSP Builder模块库工具流程,支持开发人员开发高Fmax定点或者浮点DSP设计,同时保持了基于Mathworks的仿真和开发环境的优点。要求高效能工作流程的FPGA开发人员多年以来一直使用这一产品,与经验丰富的FPGA开发人员相比,所实现的Fmax性能相同。

有你想看的精彩 基于FPGA的USB3.0 HUB设计方案基于FPGA的DDR3多端口读写存储管理系统设计基于FPGA的无线通信安全协议

扫码加微信邀请您加入FPGA学习交流群

欢迎加入至芯科技FPGA微信学习交流群,这里有一群优秀的FPGA工程师、学生、老师、这里FPGA技术交流学习氛围浓厚、相互分享、相互帮助、叫上小伙伴一起加入吧!
点个在看你最好看
原文标题:在FPGA上优化实现复数浮点计算
文章出处:【微信公众号:FPGA设计论坛】欢迎添加关注!文章转载请注明出处。
-
FPGA
+关注
关注
1635文章
21832浏览量
608117
原文标题:在FPGA上优化实现复数浮点计算
文章出处:【微信号:gh_9d70b445f494,微信公众号:FPGA设计论坛】欢迎添加关注!文章转载请注明出处。
发布评论请先 登录
相关推荐
使用OpenVINO™进行优化后,为什么DETR模型在不同的硬件上测试时显示不同的结果?
FPGA在AI方面有哪些应用
助力AIoT应用:在米尔FPGA开发板上实现Tiny YOLO V4
FPGA中的浮点四则运算是什么
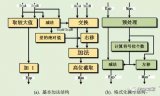
FPGA中浮点四则运算的实现过程





 在FPGA上优化实现复数浮点计算
在FPGA上优化实现复数浮点计算










评论