光波在介质中的传播可由介质中的麦克斯韦方程组精确描述。物质方程描述了感应电磁场(D、B)与电磁场(E、H)、极化场(P、M)之间的关系。不考虑非线性效应,而仅在线性光学的情形下讨论,那么极化场与电磁场之间呈线性关系。利用上述这些方程可以推导出在各向同性、均匀、无磁性、无自由电荷及电流的介质中的波动方程。电场与磁场之间存在固定的关系,所以只需要考虑电场即可,磁场可以由电场得到。
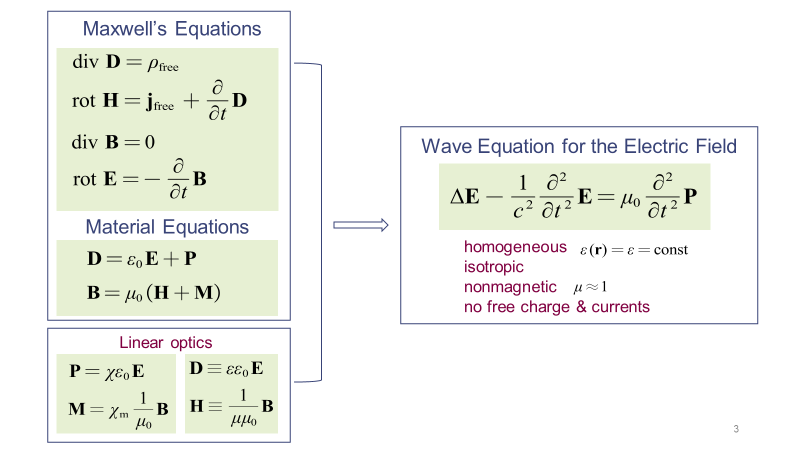
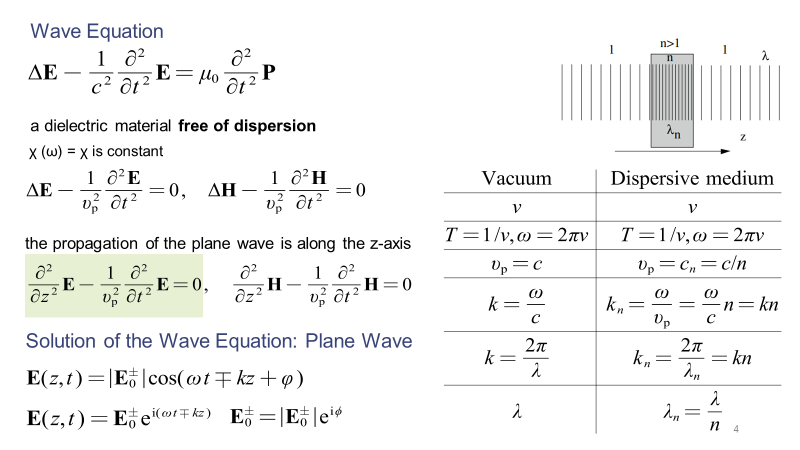
在求解波动方程时,如果不考虑介质的色散,而且假定电磁波沿z轴方向传播,那么波动方程可以进行简化。简化后的波动方程有一个最基本的特解——平面波解,而其他任何复杂的波都可以展开成平面波解的线性叠加。因此,暂时只需要讨论平面波解。平面波是一种横向电磁波,其电场、磁场的方向,以及波传播的方向三者两两垂直。当平面波从光疏介质传输到光密介质中时,其频率ν不发生变化,但是波数k、波速vp和波长λ均会发生改变。
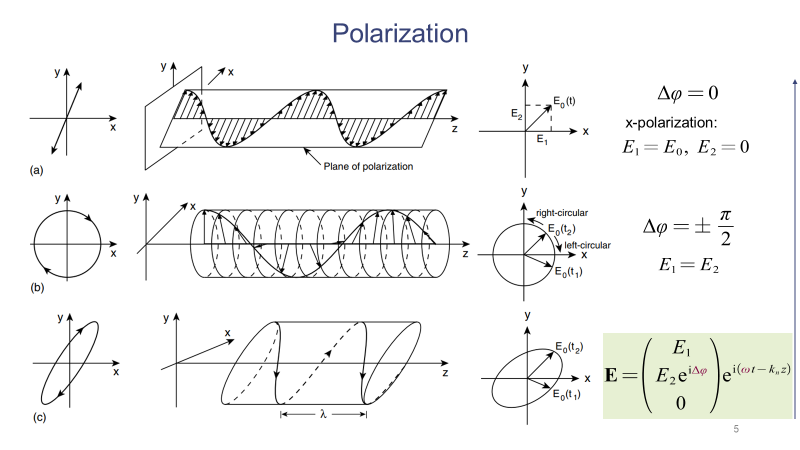
平面波的常见偏振状态可分为线偏振、圆偏振和椭圆偏振三种。最一般的情况就是椭圆偏振,这种偏振状态的电场由沿x轴和y轴两个方向、具有一定相位差且振幅任意的振动矢量叠加得到。逆着波传播的方向观察,椭圆偏振状态总的电场振动向量的轨迹是一个椭圆。当沿x轴和y轴的振动相位差为0时,总的电场振动向量的轨迹是一条线段,此时的平面波处于线偏振状态;当沿x轴和y轴的振动相位差为±π/2,且振幅相等时,总的电场振动向量的轨迹是一个圆,这样的平面波处于圆偏振状态。
电场和磁场之间的叉乘用来定义Poynting矢量,也即能流密度。对于平面波来说,能流密度矢量与传播时的等相位面垂直,即沿着波数k的方向。在计算能流密度与能量密度的瞬时值时需要注意利用的是平面波电场和磁场的实数部分;而计算能流密度与能量密度的时间平均值时,需要对代入复数电磁场后的最终结果取实部,并乘以1/2。

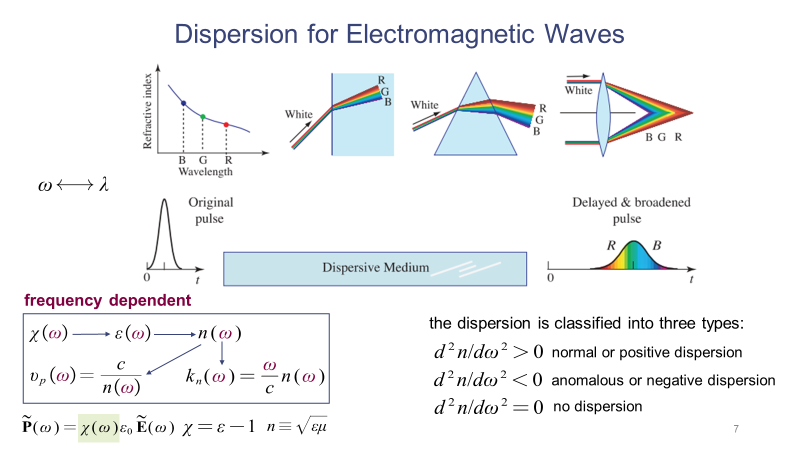
下面介绍平面波在色散介质中的传播。我们可以用两个例子来理解色散。第一个是白光光束经过介质折射后的“扩束”现象;第二个是光脉冲经过介质传播后的脉冲宽度展宽现象。这些现象源于不同频率的光在介质中传播时具有不同的折射率,使得光的偏折角度和传播速度会彼此不同。这种折射率对光频率(或波长)的依赖就导致了各种色散现象,色散现象分为三种:正常色散、反常色散和无色散。在介质正常色散的区间内,长波长的光波传播速度要比短波长的光波快,反常色散则刚好相反。
除了色散,不同光学材料拥有不同的可透光波长范围,由光学材料的吸收特性所决定。
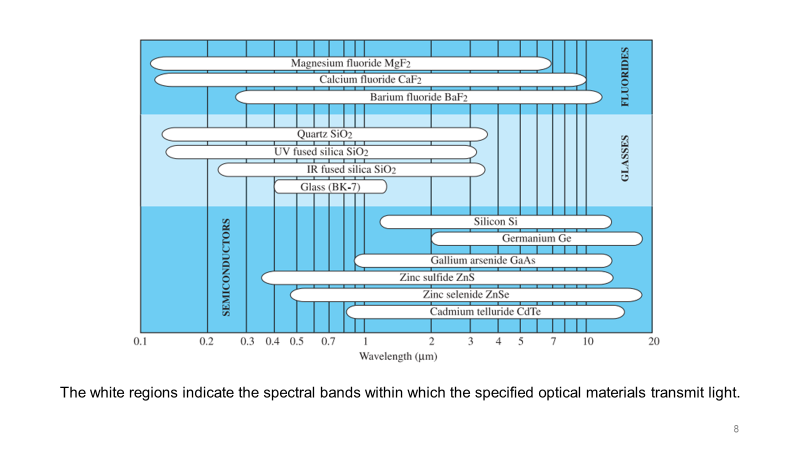
介质的色散(折射率的频率依赖性)和吸收与极化率密切相关。极化率通常为复数,其实部与折射率n相关,虚部与吸收系数α相关,并且极化率的实部和虚部满足Kramers-Kronig关系,根据这一关系,知道实部和虚部中的一个就可以得到另一个。如果所关注的波长范围远离介质的共振吸收频率,那么可以将介质的共振吸收峰近似为无限锐吸收线,也即可以用δ函数近似表示吸收系数,进而根据吸收系数α再求得折射率n的表达式,也即Sellmeier公式。
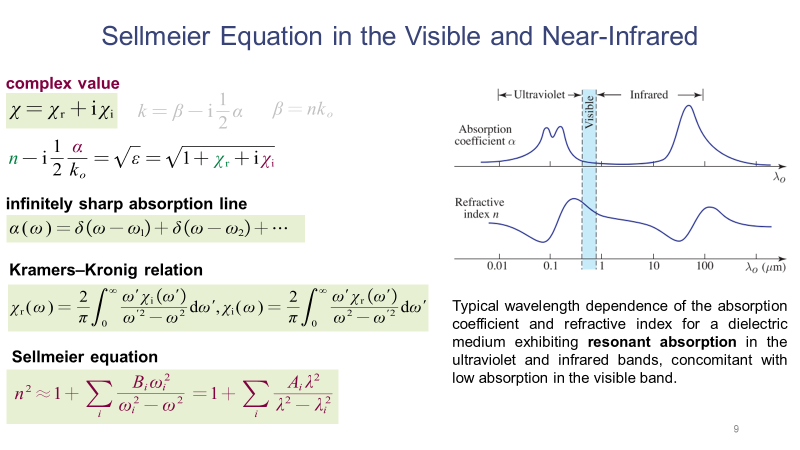
根据Sellmeier公式,对于特定的介质,当知道该式中的各个参数的值,就可以得到折射率随波长的变化关系。下面的幻灯片列举了熔融二氧化硅、SF10玻璃和蓝宝石这三种介质利用Sellmeier公式得到折射率与波长的关系曲线。
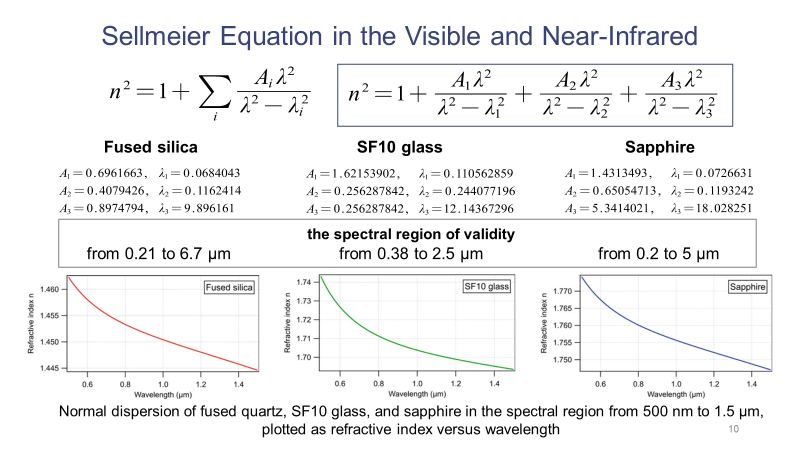
当我们关注的波长小于200nm,到达真空紫外、极紫外甚至是X射线的区域时,由于介质强烈的吸收,Sellmeier公式不再适用,这时需要利用新的计算公式来得到介质的折射率。

在计算中需要用到的各种参数也可以通过查阅工具书得到,下面的幻灯片展示了碳(C)和铝(Al)的计算结果。

以上从麦克斯韦方程组和物质方程出发,推导得到波动方程,随后讨论平面波解的特性,最后介绍平面波在色散介质中传播时的色散现象,以及在不同波长范围内如何计算介质的折射率。
审核编辑:刘清
-
电磁波
+关注
关注
21文章
1432浏览量
53679 -
电磁场
+关注
关注
0文章
785浏览量
47176
原文标题:色散介质中的平面波
文章出处:【微信号:bdtdsj,微信公众号:中科院半导体所】欢迎添加关注!文章转载请注明出处。
发布评论请先 登录
相关推荐

关于平面波导的接地孔屏蔽问题
【下载】《微波工程(第三版)》
【下载】《微波工程》
如何使用HFSS设置入射平面波?
介质透镜覆层对天线的影响分析
衍射光栅对正入射宽带平面波的响应
Ansys Lumerical衍射光栅对正入射宽带平面波响应的应用实例
平面波扬声器的应用

平面波定向广播扬声器的应用
路侧广播平面波扬声器的应用





 色散介质中的平面波介绍
色散介质中的平面波介绍











评论